Energy-Guided Decoding for Object Hallucination Mitigation

Mitigating object hallucination in large vision-language models (LVLMs) is critical to their safe deployment. Existing methods either are restricted to specific decoding methods, or demand sophisticated modifications to visual inputs, or rely on knowledge from external models. In this work, we first reveal the phenomenon that VLMs exhibit significant imbalance in the ``Yes'' ratio ( \ie, the fraction of ``Yes'' answers among the total number of questions) across three different visual question answering (VQA) datasets. Furthermore, we propose an energy-based decoding method, which dynamically selects the hidden states from the layer with minimal energy score. It is simple yet effective in reducing the bias for the yes ratio while boosting performance across three benchmarks (POPE, MME, and MMVP). Our method consistently improves accuracy and F1 score on three VQA datasets across three commonly used VLMs over several baseline methods. The average accuracy improvement is 4.82% compared to greedy decoding. Moreover, the average yes-ratio gap reduction is 8.81%, meaning the proposed method is less biased as shown in Figure 1.

Strengthening the Internal Adversarial Robustness in Lifted Neural Networks

Lifted neural networks (i.e. neural architectures explicitly optimizing over respective network potentials to determine the neural activities) can be combined with a type of adversarial training to gain robustness for internal as well as input layers, in addition to improved generalization performance. In this work we first investigate how adversarial robustness in this framework can be further strengthened by solely modifying the training loss. In a second step we fix some remaining limitations and arrive at a novel training loss for lifted neural networks, that combines targeted and untargeted adversarial perturbations.

Certifiably Optimal Anisotropic Rotation Averaging

Rotation averaging is a key subproblem in applications of computer vision and robotics. Many methods for solving this problem exist, and there are also several theoretical results analyzing difficulty and optimality. However, one aspect that most of these have in common is a focus on the isotropic setting, where the intrinsic uncertainties in the measurements are not fully incorporated into the resulting optimization task. Recent empirical results suggest that moving to an anisotropic framework, where these uncertainties are explicitly included, can result in an improvement of solution quality. However, global optimization for rotation averaging has remained a challenge in this scenario. In this paper we show how anisotropic costs can be incorporated in certifiably optimal rotation averaging. We also demonstrate how existing solvers, designed for isotropic situations, fail in the anisotropic setting. Finally, we propose a stronger relaxation and show empirically that it is able to recover global optima in all tested datasets and leads to a more accurate reconstruction in all but one of the scenes.

Text in the Dark: Extremely Low-Light Text Image Enhancement

Extremely low-light text images are common in natural scenes, making scene text detection and recognition challenging. One solution is to enhance these images using low-light image enhancement methods before text extraction. However, previous methods often do not try to particularly address the significance of low-level features, which are crucial for optimal performance on downstream scene text tasks. Further research is also hindered by the lack of extremely low-light text datasets. To address these limitations, we propose a novel encoder-decoder framework with an edge-aware attention module to focus on scene text regions during enhancement. Our proposed method uses novel text detection and edge reconstruction losses to emphasize low-level scene text features, leading to successful text extraction. Additionally, we present a Supervised Deep Curve Estimation (Supervised-DCE) model to synthesize extremely low-light images based on publicly available scene text datasets such as ICDAR15 (IC15). We also labeled texts in the extremely low-light See In the Dark (SID) and ordinary LOw-Light (LOL) datasets to allow for objective assessment of extremely low-light image enhancement through scene text tasks. Extensive experiments show that our model outperforms state-of-the-art methods in terms of both image quality and scene text metrics on the widely-used LOL, SID, and synthetic IC15 datasets. Code and dataset will be released publicly at https://github.com/chunchet-ng/Text-in-the-Dark.

Two Tales of Single-Phase Contrastive Hebbian Learning

The search for "biologically plausible" learning algorithms has converged on the idea of representing gradients as activity differences. However, most approaches require a high degree of synchronization (distinct phases during learning) and introduce substantial computational overhead, which raises doubts regarding their biological plausibility as well as their potential utility for neuromorphic computing. Furthermore, they commonly rely on applying infinitesimal perturbations (nudges) to output units, which is impractical in noisy environments. Recently it has been shown that by modelling artificial neurons as dyads with two oppositely nudged compartments, it is possible for a fully local learning algorithm named ``dual propagation'' to bridge the performance gap to backpropagation, without requiring separate learning phases or infinitesimal nudging. However, the algorithm has the drawback that its numerical stability relies on symmetric nudging, which may be restrictive in biological and analog implementations. In this work we first provide a solid foundation for the objective underlying the dual propagation method, which also reveals a surprising connection with adversarial robustness. Second, we demonstrate how dual propagation is related to a particular adjoint state method, which is stable regardless of asymmetric nudging.

Fully Variational Noise-Contrastive Estimation

By using the underlying theory of proper scoring rules, we design a family of noise-contrastive estimation (NCE) methods that are tractable for latent variable models. Both terms in the underlying NCE loss, the one using data samples and the one using noise samples, can be lower-bounded as in variational Bayes, therefore we call this family of losses fully variational noise-contrastive estimation. Variational autoencoders are a particular example in this family and therefore can be also understood as separating real data from synthetic samples using an appropriate classification loss. We further discuss other instances in this family of fully variational NCE objectives and indicate differences in their empirical behavior.

Dual Propagation: Accelerating Contrastive Hebbian Learning with Dyadic Neurons

Activity difference based learning algorithms-such as contrastive Hebbian learning and equilibrium propagation-have been proposed as biologically plausible alternatives to error back-propagation. However, on traditional digital chips these algorithms suffer from having to solve a costly inference problem twice, making these approaches more than two orders of magnitude slower than back-propagation. In the analog realm equilibrium propagation may be promising for fast and energy efficient learning, but states still need to be inferred and stored twice. Inspired by lifted neural networks and compartmental neuron models we propose a simple energy based compartmental neuron model, termed dual propagation, in which each neuron is a dyad with two intrinsic states. At inference time these intrinsic states encode the error/activity duality through their difference and their mean respectively. The advantage of this method is that only a single inference phase is needed and that inference can be solved in layerwise closed-form. Experimentally we show on common computer vision datasets, including Imagenet32x32, that dual propagation performs equivalently to back-propagation both in terms of accuracy and runtime.

Extremely Low-light Image Enhancement with Scene Text Restoration

Deep learning-based methods have made impressive progress in enhancing extremely low-light images - the image quality of the reconstructed images has generally improved. However, we found out that most of these methods could not sufficiently recover the image details, for instance, the texts in the scene. In this paper, a novel image enhancement framework is proposed to precisely restore the scene texts, as well as the overall quality of the image simultaneously under extremely low-light images conditions. Mainly, we employed a self-regularised attention map, an edge map, and a novel text detection loss. In addition, leveraging synthetic low-light images is beneficial for image enhancement on the genuine ones in terms of text detection. The quantitative and qualitative experimental results have shown that the proposed model outperforms state-of-the-art methods in image restoration, text detection, and text spotting on See In the Dark and ICDAR15 datasets.

AdaSTE: An Adaptive Straight-Through Estimator to Train Binary Neural Networks

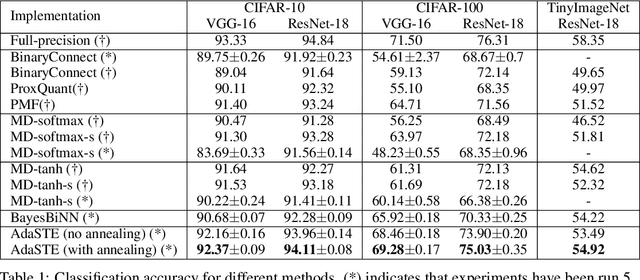
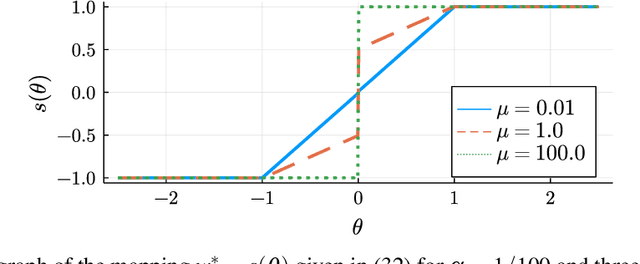
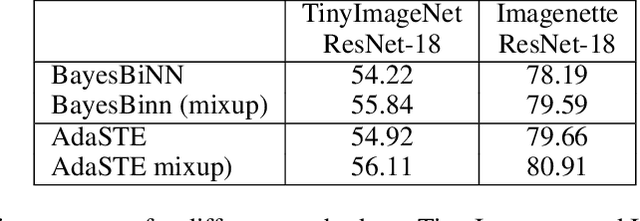
We propose a new algorithm for training deep neural networks (DNNs) with binary weights. In particular, we first cast the problem of training binary neural networks (BiNNs) as a bilevel optimization instance and subsequently construct flexible relaxations of this bilevel program. The resulting training method shares its algorithmic simplicity with several existing approaches to train BiNNs, in particular with the straight-through gradient estimator successfully employed in BinaryConnect and subsequent methods. In fact, our proposed method can be interpreted as an adaptive variant of the original straight-through estimator that conditionally (but not always) acts like a linear mapping in the backward pass of error propagation. Experimental results demonstrate that our new algorithm offers favorable performance compared to existing approaches.

BabelCalib: A Universal Approach to Calibrating Central Cameras

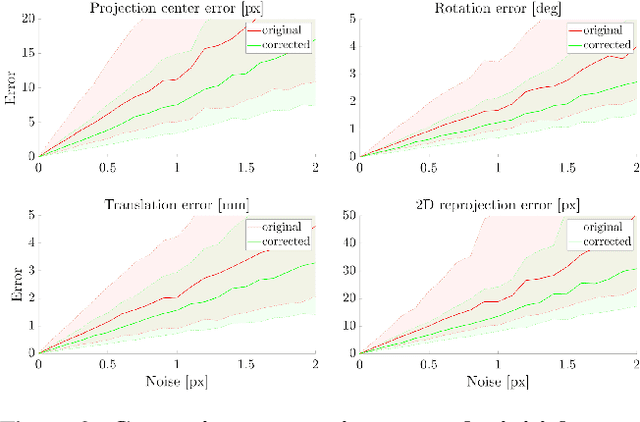
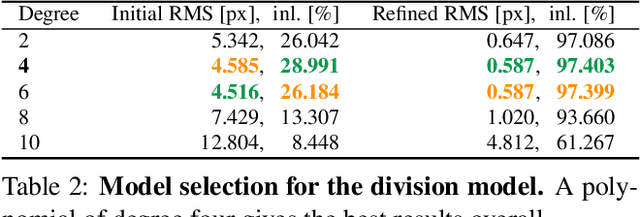
Existing calibration methods occasionally fail for large field-of-view cameras due to the non-linearity of the underlying problem and the lack of good initial values for all parameters of the used camera model. This might occur because a simpler projection model is assumed in an initial step, or a poor initial guess for the internal parameters is pre-defined. A lot of the difficulties of general camera calibration lie in the use of a forward projection model. We side-step these challenges by first proposing a solver to calibrate the parameters in terms of a back-projection model and then regress the parameters for a target forward model. These steps are incorporated in a robust estimation framework to cope with outlying detections. Extensive experiments demonstrate that our approach is very reliable and returns the most accurate calibration parameters as measured on the downstream task of absolute pose estimation on test sets. The code is released at https://github.com/ylochman/babelcalib.