Two Tales of Single-Phase Contrastive Hebbian Learning

The search for "biologically plausible" learning algorithms has converged on the idea of representing gradients as activity differences. However, most approaches require a high degree of synchronization (distinct phases during learning) and introduce substantial computational overhead, which raises doubts regarding their biological plausibility as well as their potential utility for neuromorphic computing. Furthermore, they commonly rely on applying infinitesimal perturbations (nudges) to output units, which is impractical in noisy environments. Recently it has been shown that by modelling artificial neurons as dyads with two oppositely nudged compartments, it is possible for a fully local learning algorithm named ``dual propagation'' to bridge the performance gap to backpropagation, without requiring separate learning phases or infinitesimal nudging. However, the algorithm has the drawback that its numerical stability relies on symmetric nudging, which may be restrictive in biological and analog implementations. In this work we first provide a solid foundation for the objective underlying the dual propagation method, which also reveals a surprising connection with adversarial robustness. Second, we demonstrate how dual propagation is related to a particular adjoint state method, which is stable regardless of asymmetric nudging.

AdaSTE: An Adaptive Straight-Through Estimator to Train Binary Neural Networks

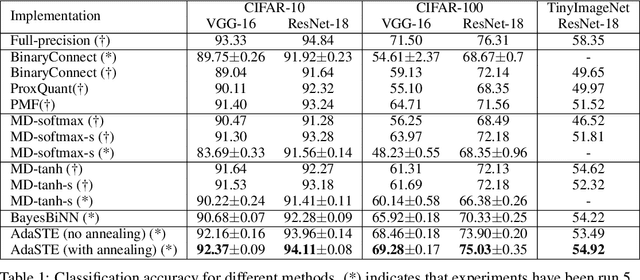
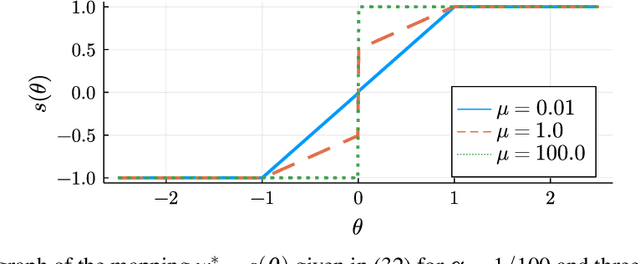
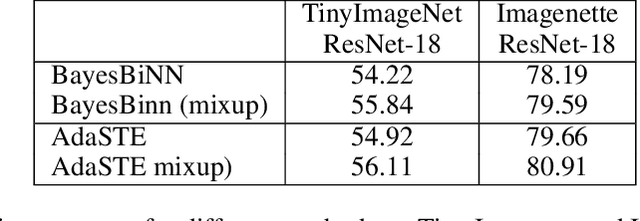
We propose a new algorithm for training deep neural networks (DNNs) with binary weights. In particular, we first cast the problem of training binary neural networks (BiNNs) as a bilevel optimization instance and subsequently construct flexible relaxations of this bilevel program. The resulting training method shares its algorithmic simplicity with several existing approaches to train BiNNs, in particular with the straight-through gradient estimator successfully employed in BinaryConnect and subsequent methods. In fact, our proposed method can be interpreted as an adaptive variant of the original straight-through estimator that conditionally (but not always) acts like a linear mapping in the backward pass of error propagation. Experimental results demonstrate that our new algorithm offers favorable performance compared to existing approaches.

Lifted Regression/Reconstruction Networks

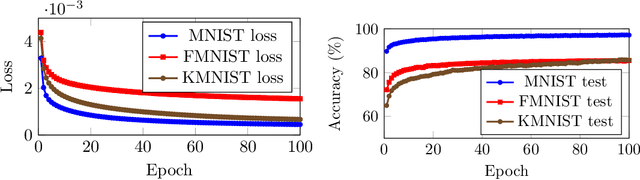
In this work we propose lifted regression/reconstruction networks (LRRNs), which combine lifted neural networks with a guaranteed Lipschitz continuity property for the output layer. Lifted neural networks explicitly optimize an energy model to infer the unit activations and therefore---in contrast to standard feed-forward neural networks---allow bidirectional feedback between layers. So far lifted neural networks have been modelled around standard feed-forward architectures. We propose to take further advantage of the feedback property by letting the layers simultaneously perform regression and reconstruction. The resulting lifted network architecture allows to control the desired amount of Lipschitz continuity, which is an important feature to obtain adversarially robust regression and classification methods. We analyse and numerically demonstrate applications for unsupervised and supervised learning.