Lifted Regression/Reconstruction Networks
Paper and Code
May 07, 2020

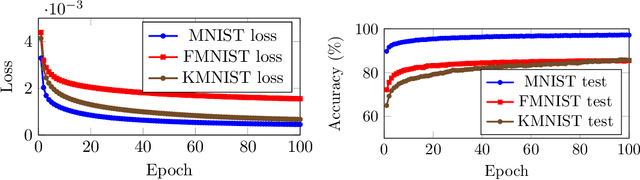

In this work we propose lifted regression/reconstruction networks (LRRNs), which combine lifted neural networks with a guaranteed Lipschitz continuity property for the output layer. Lifted neural networks explicitly optimize an energy model to infer the unit activations and therefore---in contrast to standard feed-forward neural networks---allow bidirectional feedback between layers. So far lifted neural networks have been modelled around standard feed-forward architectures. We propose to take further advantage of the feedback property by letting the layers simultaneously perform regression and reconstruction. The resulting lifted network architecture allows to control the desired amount of Lipschitz continuity, which is an important feature to obtain adversarially robust regression and classification methods. We analyse and numerically demonstrate applications for unsupervised and supervised learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge