GeM-NR: Geometry-Aware Multi-View Editing for Nonrigid Scene Changes

Recent developments in multi-view image editing with generative models have brought us a step closer toward general 3D content generation and customization. Most existing works focus on rigid or appearance-only edits by utilizing the geometry of the unedited scene. This naturally limits these methods to edits that preserve the underlying scene structure. Other approaches are trained for specific image editing tasks, such as object removal and addition. Despite this progress, general nonrigid edits, i.e., edits that substantially change the scene geometry, remain challenging for existing methods. We propose GeM-NR, a fast and flexible training-free approach for general multi-view consistent image editing, including edits that drastically change the geometry and appearance of the scene. Given an anchor image edited with a chosen backbone editor (such as FLUX, Qwen, BrushNet) and a query unedited image, GeM-NR edits the query image consistently with the anchor edit. The method incorporates multiple stages: (i) depth map estimation, where we propose a strategy to maximize the alignment between the 3D point clouds of the edited and unedited scenes, (ii) projection onto a query viewpoint, and (iii) refinement of the obtained image conditioned on the unedited query. The conditioning-based formulation scales well from two to many views of an object. We demonstrate the ability of our method to handle edits with significant changes in geometry and appearance, something that existing methods struggle with. We perform an extensive evaluation showing that our method improves consistency for a wide variety of edit tasks, including generating 3D representations of the edited scene. Both quantitative and qualitative results indicate the state-of-the-art performance of our method in terms of edit quality as well as geometric and photometric consistency across multiple views.

Certifiably Optimal Anisotropic Rotation Averaging

Rotation averaging is a key subproblem in applications of computer vision and robotics. Many methods for solving this problem exist, and there are also several theoretical results analyzing difficulty and optimality. However, one aspect that most of these have in common is a focus on the isotropic setting, where the intrinsic uncertainties in the measurements are not fully incorporated into the resulting optimization task. Recent empirical results suggest that moving to an anisotropic framework, where these uncertainties are explicitly included, can result in an improvement of solution quality. However, global optimization for rotation averaging has remained a challenge in this scenario. In this paper we show how anisotropic costs can be incorporated in certifiably optimal rotation averaging. We also demonstrate how existing solvers, designed for isotropic situations, fail in the anisotropic setting. Finally, we propose a stronger relaxation and show empirically that it is able to recover global optima in all tested datasets and leads to a more accurate reconstruction in all but one of the scenes.

BabelCalib: A Universal Approach to Calibrating Central Cameras

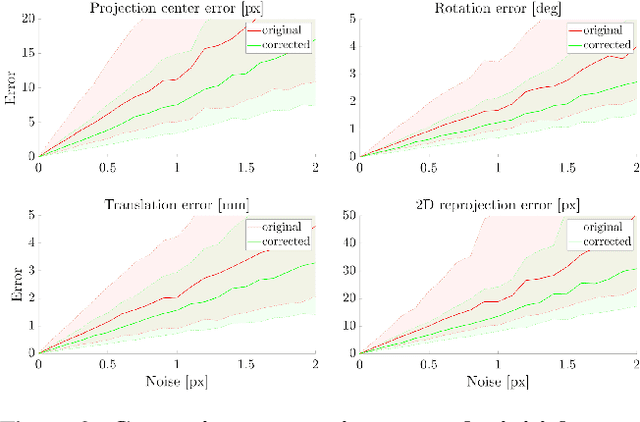
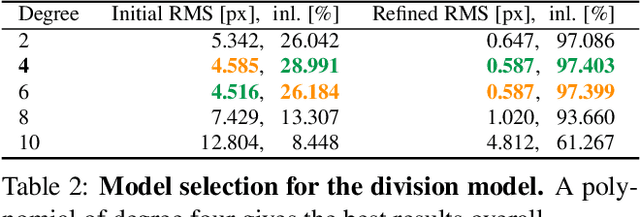
Existing calibration methods occasionally fail for large field-of-view cameras due to the non-linearity of the underlying problem and the lack of good initial values for all parameters of the used camera model. This might occur because a simpler projection model is assumed in an initial step, or a poor initial guess for the internal parameters is pre-defined. A lot of the difficulties of general camera calibration lie in the use of a forward projection model. We side-step these challenges by first proposing a solver to calibrate the parameters in terms of a back-projection model and then regress the parameters for a target forward model. These steps are incorporated in a robust estimation framework to cope with outlying detections. Extensive experiments demonstrate that our approach is very reliable and returns the most accurate calibration parameters as measured on the downstream task of absolute pose estimation on test sets. The code is released at https://github.com/ylochman/babelcalib.

Minimal Solvers for Single-View Lens-Distorted Camera Auto-Calibration

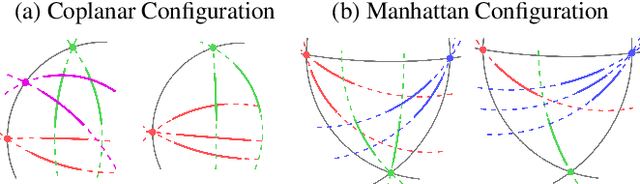
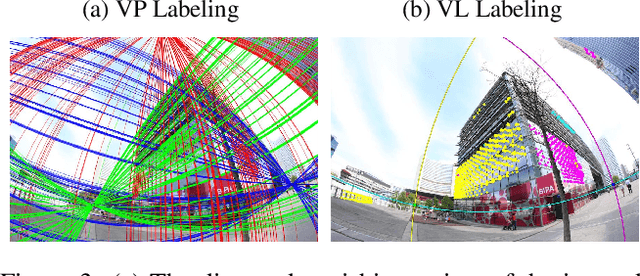
This paper proposes minimal solvers that use combinations of imaged translational symmetries and parallel scene lines to jointly estimate lens undistortion with either affine rectification or focal length and absolute orientation. We use constraints provided by orthogonal scene planes to recover the focal length. We show that solvers using feature combinations can recover more accurate calibrations than solvers using only one feature type on scenes that have a balance of lines and texture. We also show that the proposed solvers are complementary and can be used together in a RANSAC-based estimator to improve auto-calibration accuracy. State-of-the-art performance is demonstrated on a standard dataset of lens-distorted urban images. The code is available at https://github.com/ylochman/single-view-autocalib.

Minimal Solvers for Rectifying from Radially-Distorted Conjugate Translations

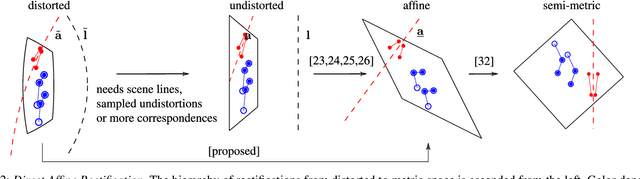
This paper introduces minimal solvers that jointly solve for affine-rectification and radial lens undistortion from the image of translated and reflected coplanar features. The proposed solvers use the invariant that the affine-rectified image of the meet of the joins of radially-distorted conjugately-translated point correspondences is on the line at infinity. The hidden-variable trick from algebraic geometry is used to reformulate and simplify the constraints so that the generated solvers are stable, small and fast. Multiple solvers are proposed to accommodate various local feature types and sampling strategies, and, remarkably, three of the proposed solvers can recover rectification and lens undistortion from only one radially-distorted conjugately-translated affine-covariant region correspondence. Synthetic and real-image experiments confirm that the proposed solvers demonstrate superior robustness to noise compared to the state of the art. Accurate rectifications on imagery taken with narrow to fisheye field-of-view lenses demonstrate the wide applicability of the proposed method. The method is fully automatic.

Minimal Solvers for Rectifying from Radially-Distorted Scales and Change of Scales

This paper introduces the first minimal solvers that jointly estimate lens distortion and affine rectification from the image of rigidly-transformed coplanar features. The solvers work on scenes without straight lines and, in general, relax strong assumptions about scene content made by the state of the art. The proposed solvers use the affine invariant that coplanar repeats have the same scale in rectified space. The solvers are separated into two groups that differ by how the equal scale invariant of rectified space is used to place constraints on the lens undistortion and rectification parameters. We demonstrate a principled approach for generating stable minimal solvers by the Gr\"obner basis method, which is accomplished by sampling feasible monomial bases to maximize numerical stability. Synthetic and real-image experiments confirm that the proposed solvers demonstrate superior robustness to noise compared to the state of the art. Accurate rectifications on imagery taken with narrow to fisheye field-of-view lenses demonstrate the wide applicability of the proposed method. The method is fully automatic.