On the Tightness of Semidefinite Relaxations for Rotation Estimation
Paper and Code
Jan 06, 2021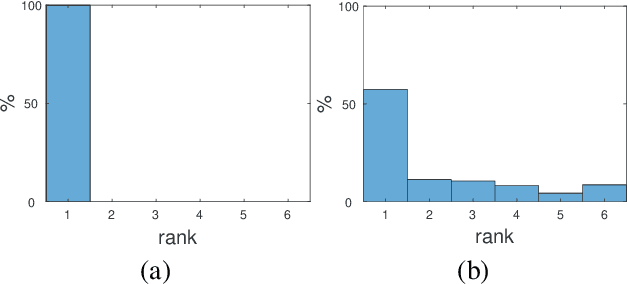


Why is it that semidefinite relaxations have been so successful in numerous applications in computer vision and robotics for solving non-convex optimization problems involving rotations? In studying the empirical performance, we note that there are hardly any failure cases reported in the literature, motivating us to approach these problems from a theoretical perspective. A general framework based on tools from algebraic geometry is introduced for analyzing the power of semidefinite relaxations of problems with quadratic objective functions and rotational constraints. Applications include registration, hand-eye calibration, camera resectioning and rotation averaging. We characterize the extreme points, and show that there are plenty of failure cases for which the relaxation is not tight, even in the case of a single rotation. We also show that for some problem classes, an appropriate rotation parametrization guarantees tight relaxations. Our theoretical findings are accompanied with numerical simulations, providing further evidence and understanding of the results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge