Learning Structure-from-Motion with Graph Attention Networks

In this paper we tackle the problem of learning Structure-from-Motion (SfM) through the use of graph attention networks. SfM is a classic computer vision problem that is solved though iterative minimization of reprojection errors, referred to as Bundle Adjustment (BA), starting from a good initialization. In order to obtain a good enough initialization to BA, conventional methods rely on a sequence of sub-problems (such as pairwise pose estimation, pose averaging or triangulation) which provides an initial solution that can then be refined using BA. In this work we replace these sub-problems by learning a model that takes as input the 2D keypoints detected across multiple views, and outputs the corresponding camera poses and 3D keypoint coordinates. Our model takes advantage of graph neural networks to learn SfM-specific primitives, and we show that it can be used for fast inference of the reconstruction for new and unseen sequences. The experimental results show that the proposed model outperforms competing learning-based methods, and challenges COLMAP while having lower runtime.

On the Tightness of Semidefinite Relaxations for Rotation Estimation

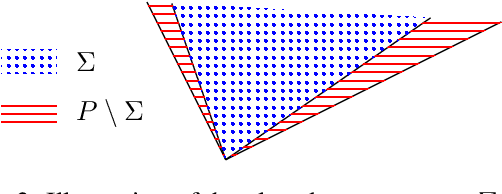
Why is it that semidefinite relaxations have been so successful in numerous applications in computer vision and robotics for solving non-convex optimization problems involving rotations? In studying the empirical performance, we note that there are hardly any failure cases reported in the literature, motivating us to approach these problems from a theoretical perspective. A general framework based on tools from algebraic geometry is introduced for analyzing the power of semidefinite relaxations of problems with quadratic objective functions and rotational constraints. Applications include registration, hand-eye calibration, camera resectioning and rotation averaging. We characterize the extreme points, and show that there are plenty of failure cases for which the relaxation is not tight, even in the case of a single rotation. We also show that for some problem classes, an appropriate rotation parametrization guarantees tight relaxations. Our theoretical findings are accompanied with numerical simulations, providing further evidence and understanding of the results.

Accurate Optimization of Weighted Nuclear Norm for Non-Rigid Structure from Motion

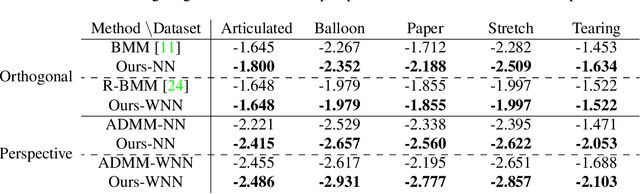
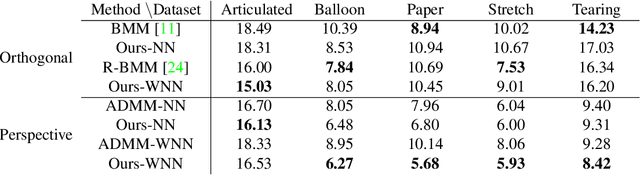
Fitting a matrix of a given rank to data in a least squares sense can be done very effectively using 2nd order methods such as Levenberg-Marquardt by explicitly optimizing over a bilinear parameterization of the matrix. In contrast, when applying more general singular value penalties, such as weighted nuclear norm priors, direct optimization over the elements of the matrix is typically used. Due to non-differentiability of the resulting objective function, first order sub-gradient or splitting methods are predominantly used. While these offer rapid iterations it is well known that they become inefficent near the minimum due to zig-zagging and in practice one is therefore often forced to settle for an approximate solution. In this paper we show that more accurate results can in many cases be achieved with 2nd order methods. Our main result shows how to construct bilinear formulations, for a general class of regularizers including weighted nuclear norm penalties, that are provably equivalent to the original problems. With these formulations the regularizing function becomes twice differentiable and 2nd order methods can be applied. We show experimentally, on a number of structure from motion problems, that our approach outperforms state-of-the-art methods.