Learning Structure-from-Motion with Graph Attention Networks

In this paper we tackle the problem of learning Structure-from-Motion (SfM) through the use of graph attention networks. SfM is a classic computer vision problem that is solved though iterative minimization of reprojection errors, referred to as Bundle Adjustment (BA), starting from a good initialization. In order to obtain a good enough initialization to BA, conventional methods rely on a sequence of sub-problems (such as pairwise pose estimation, pose averaging or triangulation) which provides an initial solution that can then be refined using BA. In this work we replace these sub-problems by learning a model that takes as input the 2D keypoints detected across multiple views, and outputs the corresponding camera poses and 3D keypoint coordinates. Our model takes advantage of graph neural networks to learn SfM-specific primitives, and we show that it can be used for fast inference of the reconstruction for new and unseen sequences. The experimental results show that the proposed model outperforms competing learning-based methods, and challenges COLMAP while having lower runtime.

Rigidity Preserving Image Transformations and Equivariance in Perspective

We characterize the class of image plane transformations which realize rigid camera motions and call these transformations `rigidity preserving'. In particular, 2D translations of pinhole images are not rigidity preserving. Hence, when using CNNs for 3D inference tasks, it can be beneficial to modify the inductive bias from equivariance towards translations to equivariance towards rigidity preserving transformations. We investigate how equivariance with respect to rigidity preserving transformations can be approximated in CNNs, and test our ideas on both 6D object pose estimation and visual localization. Experimentally, we improve on several competitive baselines.

On the Tightness of Semidefinite Relaxations for Rotation Estimation

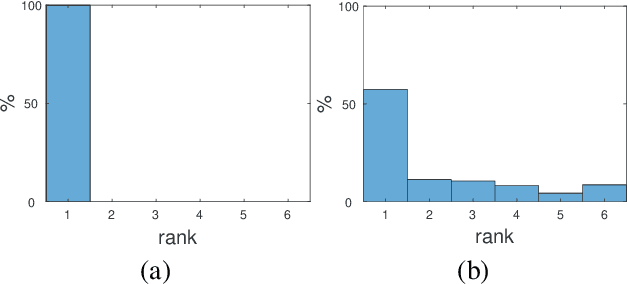
Why is it that semidefinite relaxations have been so successful in numerous applications in computer vision and robotics for solving non-convex optimization problems involving rotations? In studying the empirical performance, we note that there are hardly any failure cases reported in the literature, motivating us to approach these problems from a theoretical perspective. A general framework based on tools from algebraic geometry is introduced for analyzing the power of semidefinite relaxations of problems with quadratic objective functions and rotational constraints. Applications include registration, hand-eye calibration, camera resectioning and rotation averaging. We characterize the extreme points, and show that there are plenty of failure cases for which the relaxation is not tight, even in the case of a single rotation. We also show that for some problem classes, an appropriate rotation parametrization guarantees tight relaxations. Our theoretical findings are accompanied with numerical simulations, providing further evidence and understanding of the results.

Pose Proposal Critic: Robust Pose Refinement by Learning Reprojection Errors

In recent years, considerable progress has been made for the task of rigid object pose estimation from a single RGB-image, but achieving robustness to partial occlusions remains a challenging problem. Pose refinement via rendering has shown promise in order to achieve improved results, in particular, when data is scarce. In this paper we focus our attention on pose refinement, and show how to push the state-of-the-art further in the case of partial occlusions. The proposed pose refinement method leverages on a simplified learning task, where a CNN is trained to estimate the reprojection error between an observed and a rendered image. We experiment by training on purely synthetic data as well as a mixture of synthetic and real data. Current state-of-the-art results are outperformed for two out of three metrics on the Occlusion LINEMOD benchmark, while performing on-par for the final metric.