Data Augmentation and Regularization for Learning Group Equivariance

In many machine learning tasks, known symmetries can be used as an inductive bias to improve model performance. In this paper, we consider learning group equivariance through training with data augmentation. We summarize results from a previous paper of our own, and extend the results to show that equivariance of the trained model can be achieved through training on augmented data in tandem with regularization.

Ensembles provably learn equivariance through data augmentation

Recently, it was proved that group equivariance emerges in ensembles of neural networks as the result of full augmentation in the limit of infinitely wide neural networks (neural tangent kernel limit). In this paper, we extend this result significantly. We provide a proof that this emergence does not depend on the neural tangent kernel limit at all. We also consider stochastic settings, and furthermore general architectures. For the latter, we provide a simple sufficient condition on the relation between the architecture and the action of the group for our results to hold. We validate our findings through simple numeric experiments.

Optimization Dynamics of Equivariant and Augmented Neural Networks

We investigate the optimization of multilayer perceptrons on symmetric data. We compare the strategy of constraining the architecture to be equivariant to that of using augmentation. We show that, under natural assumptions on the loss and non-linearities, the sets of equivariant stationary points are identical for the two strategies, and that the set of equivariant layers is invariant under the gradient flow for augmented models. Finally, we show that stationary points may be unstable for augmented training although they are stable for the equivariant models

In Search of Projectively Equivariant Neural Networks

Equivariance of linear neural network layers is well studied. In this work, we relax the equivariance condition to only be true in a projective sense. In particular, we study the relation of projective and ordinary equivariance and show that for important examples, the problems are in fact equivalent. The rotation group in 3D acts projectively on the projective plane. We experimentally study the practical importance of rotation equivariance when designing networks for filtering 2D-2D correspondences. Fully equivariant models perform poorly, and while a simple addition of invariant features to a strong baseline yields improvements, this seems to not be due to improved equivariance.

One-Shot Messaging at Any Load Through Random Sub-Channeling in OFDM

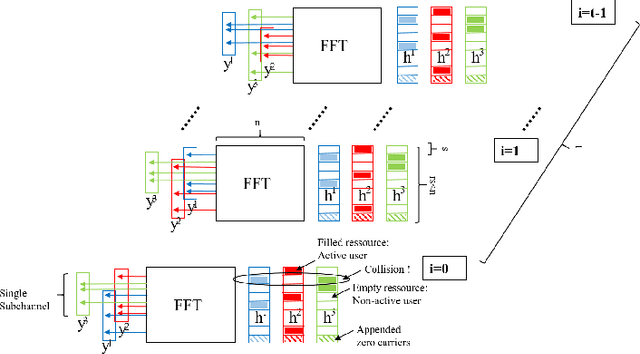
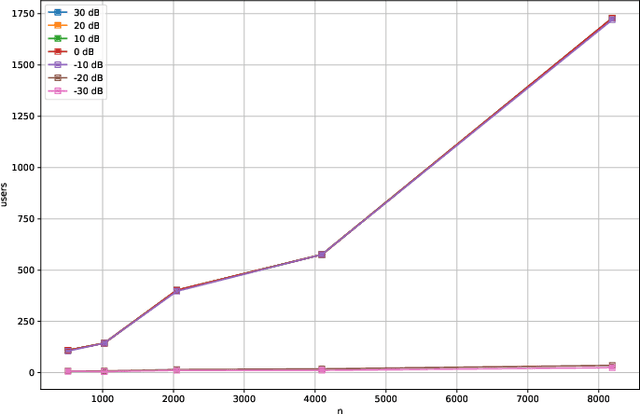
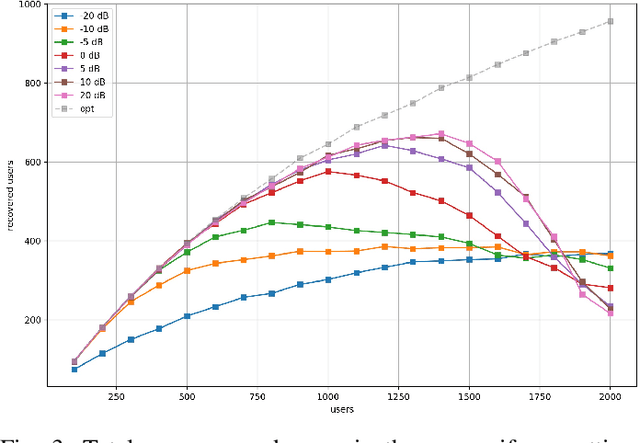
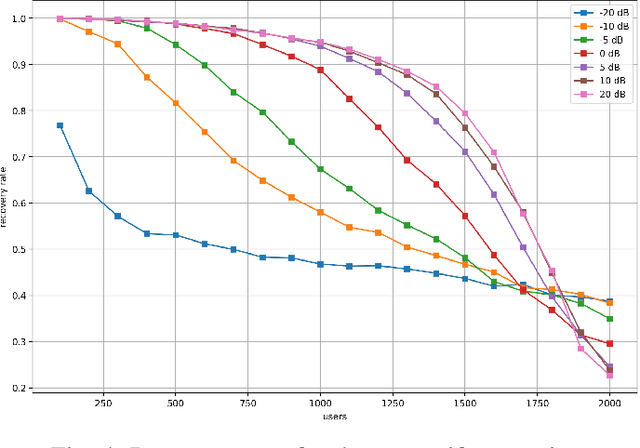
Compressive Sensing has well boosted massive random access protocols over the last decade. In this paper we apply an orthogonal FFT basis as it is used in OFDM, but subdivide its image into so-called sub-channels and let each sub-channel take only a fraction of the load. In a random fashion the subdivision is consecutively applied over a suitable number of time-slots. Within the time-slots the users will not change their sub-channel assignment and send in parallel the data. Activity detection is carried out jointly across time-slots in each of the sub-channels. For such system design we derive three rather fundamental results: i) First, we prove that the subdivision can be driven to the extent that the activity in each sub-channel is sparse by design. An effect that we call sparsity capture effect. ii) Second, we prove that effectively the system can sustain any overload situation relative to the FFT dimension, i.e. detection failure of active and non-active users can be kept below any desired threshold regardless of the number of users. The only price to pay is delay, i.e. the number of time-slots over which cross-detection is performed. We achieve this by jointly exploring the effect of measure concentration in time and frequency and careful system parameter scaling. iii) Third, we prove that parallel to activity detection active users can carry one symbol per pilot resource and time-slot so it supports so-called one-shot messaging. The key to proving these results are new concentration results for sequences of randomly sub-sampled FFTs detecting the sparse vectors "en bloc". Eventually, we show by simulations that the system is scalable resulting in a coarsely 30-fold capacity increase compared to standard OFDM.

Rigidity Preserving Image Transformations and Equivariance in Perspective

We characterize the class of image plane transformations which realize rigid camera motions and call these transformations `rigidity preserving'. In particular, 2D translations of pinhole images are not rigidity preserving. Hence, when using CNNs for 3D inference tasks, it can be beneficial to modify the inductive bias from equivariance towards translations to equivariance towards rigidity preserving transformations. We investigate how equivariance with respect to rigidity preserving transformations can be approximated in CNNs, and test our ideas on both 6D object pose estimation and visual localization. Experimentally, we improve on several competitive baselines.

ZZ-Net: A Universal Rotation Equivariant Architecture for 2D Point Clouds

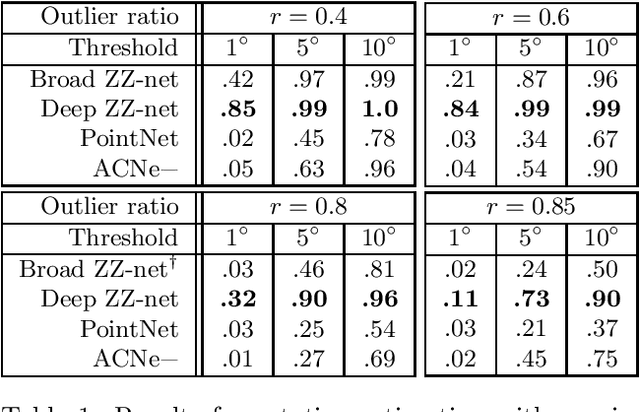
In this paper, we are concerned with rotation equivariance on 2D point cloud data. We describe a particular set of functions able to approximate any continuous rotation equivariant and permutation invariant function. Based on this result, we propose a novel neural network architecture for processing 2D point clouds and we prove its universality for approximating functions exhibiting these symmetries. We also show how to extend the architecture to accept a set of 2D-2D correspondences as indata, while maintaining similar equivariance properties. Experiments are presented on the estimation of essential matrices in stereo vision.

Measure Concentration on the OFDM-based Random Access Channel

It is well known that CS can boost massive random access protocols. Usually, the protocols operate in some overloaded regime where the sparsity can be exploited. In this paper, we consider a different approach by taking an orthogonal FFT base, subdivide its image into appropriate sub-channels and let each subchannel take only a fraction of the load. To show that this approach can actually achieve the full capacity we provide i) new concentration inequalities, and ii) devise a sparsity capture effect, i.e where the sub-division can be driven such that the activity in each each sub-channel is sparse by design. We show by simulations that the system is scalable resulting in a coarsely 30-fold capacity increase.

Hierarchical sparse recovery from hierarchically structured measurements with application to massive random access

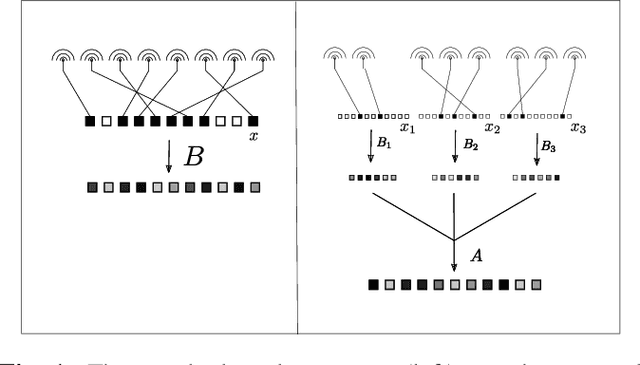
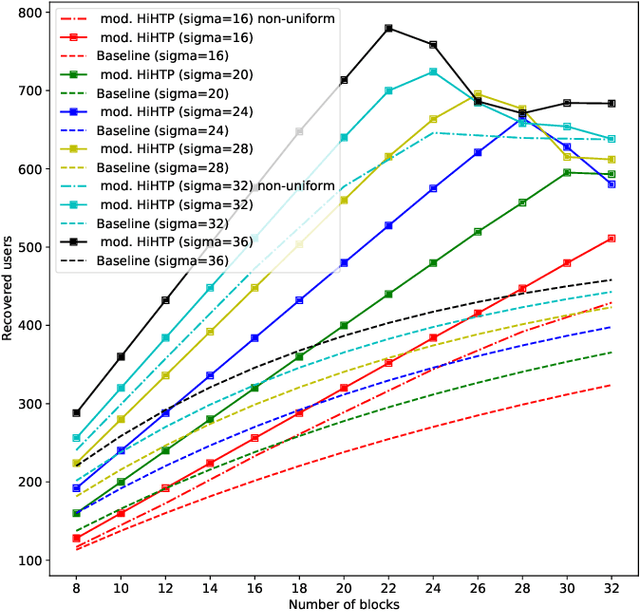
A new family of operators, coined hierarchical measurement operators, is introduced and discussed within the well-known hierarchical sparse recovery framework. Such operator is a composition of block and mixing operations and notably contains the Kronecker product as a special case. Results on their hierarchical restricted isometry property (HiRIP) are derived, generalizing prior work on recovery of hierarchically sparse signals from Kronecker-structured linear measurements. Specifically, these results show that, very surprisingly, sparsity properties of the block and mixing part can be traded against each other. The measurement structure is well-motivated by a massive random access channel design in communication engineering. Numerical evaluation of user detection rates demonstrate the huge benefit of the theoretical framework.

Hierarchical compressed sensing

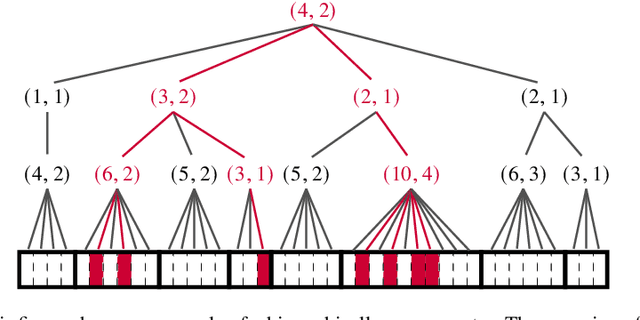
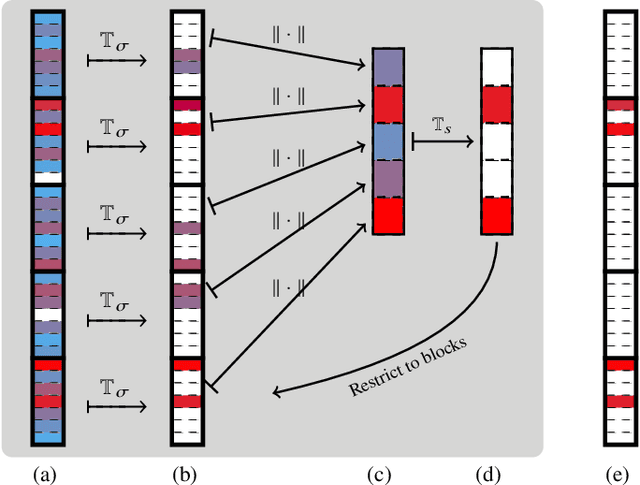
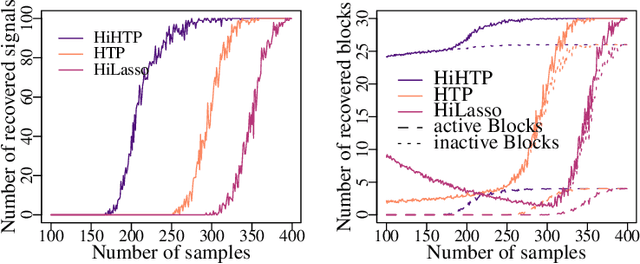
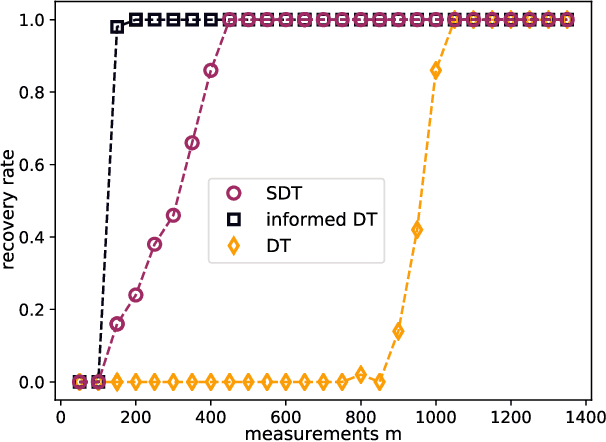
Compressed sensing is a paradigm within signal processing that provides the means for recovering structured signals from linear measurements in a highly efficient manner. Originally devised for the recovery of sparse signals, it has become clear that a similar methodology would also carry over to a wealth of other classes of structured signals. In this work, we provide an overview over the theory of compressed sensing for a particularly rich family of such signals, namely those of hierarchically structured signals. Examples of such signals are constituted by blocked vectors, with only few non-vanishing sparse blocks. We present recovery algorithms based on efficient hierarchical hard-thresholding. The algorithms are guaranteed to stable and robustly converge to the correct solution provide the measurement map acts isometrically restricted to the signal class. We then provide a series of results establishing that the required condition for large classes of measurement ensembles. Building upon this machinery, we sketch practical applications of this framework in machine-type and quantum communication.