ALIGN-FL: Architecture-independent Learning through Invariant Generative component sharing in Federated Learning

We present ALIGN-FL, a novel approach to distributed learning that addresses the challenge of learning from highly disjoint data distributions through selective sharing of generative components. Instead of exchanging full model parameters, our framework enables privacy-preserving learning by transferring only generative capabilities across clients, while the server performs global training using synthetic samples. Through complementary privacy mechanisms: DP-SGD with adaptive clipping and Lipschitz regularized VAE decoders and a stateful architecture supporting heterogeneous clients, we experimentally validate our approach on MNIST and Fashion-MNIST datasets with cross-domain outliers. Our analysis demonstrates that both privacy mechanisms effectively map sensitive outliers to typical data points while maintaining utility in extreme Non-IID scenarios typical of cross-silo collaborations. Index Terms: Client-invariant Learning, Federated Learning (FL), Privacy-preserving Generative Models, Non-Independent and Identically Distributed (Non-IID), Heterogeneous Architectures

Tracking UWB Devices Through Radio Frequency Fingerprinting Is Possible

Ultra-wideband (UWB) is a state-of-the-art technology designed for applications requiring centimeter-level localization. Its widespread adoption by smartphone manufacturer naturally raises security and privacy concerns. Successfully implementing Radio Frequency Fingerprinting (RFF) to UWB could enable physical layer security, but might also allow undesired tracking of the devices. The scope of this paper is to explore the feasibility of applying RFF to UWB and investigates how well this technique generalizes across different environments. We collected a realistic dataset using off-the-shelf UWB devices with controlled variation in device positioning. Moreover, we developed an improved deep learning pipeline to extract the hardware signature from the signal data. In stable conditions, the extracted RFF achieves over 99% accuracy. While the accuracy decreases in more changing environments, we still obtain up to 76% accuracy in untrained locations.

Differentially Private Synthetic Data Generation via Lipschitz-Regularised Variational Autoencoders

Synthetic data has been hailed as the silver bullet for privacy preserving data analysis. If a record is not real, then how could it violate a person's privacy? In addition, deep-learning based generative models are employed successfully to approximate complex high-dimensional distributions from data and draw realistic samples from this learned distribution. It is often overlooked though that generative models are prone to memorising many details of individual training records and often generate synthetic data that too closely resembles the underlying sensitive training data, hence violating strong privacy regulations as, e.g., encountered in health care. Differential privacy is the well-known state-of-the-art framework for guaranteeing protection of sensitive individuals' data, allowing aggregate statistics and even machine learning models to be released publicly without compromising privacy. The training mechanisms however often add too much noise during the training process, and thus severely compromise the utility of these private models. Even worse, the tight privacy budgets do not allow for many training epochs so that model quality cannot be properly controlled in practice. In this paper we explore an alternative approach for privately generating data that makes direct use of the inherent stochasticity in generative models, e.g., variational autoencoders. The main idea is to appropriately constrain the continuity modulus of the deep models instead of adding another noise mechanism on top. For this approach, we derive mathematically rigorous privacy guarantees and illustrate its effectiveness with practical experiments.

One-Shot Messaging at Any Load Through Random Sub-Channeling in OFDM

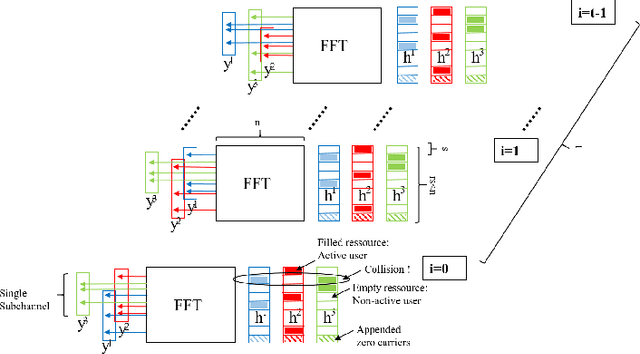
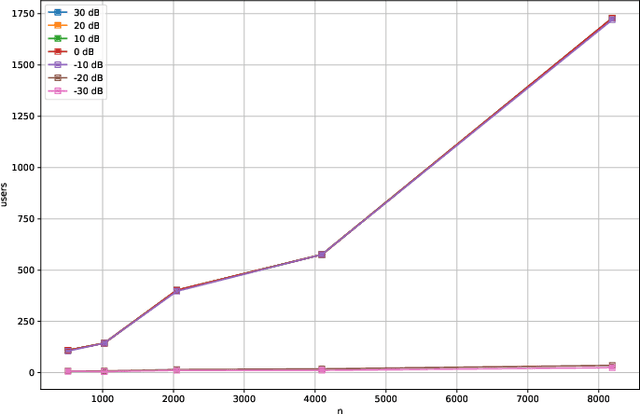
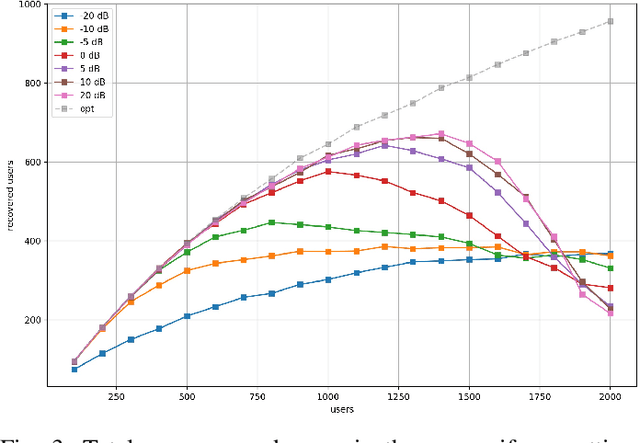
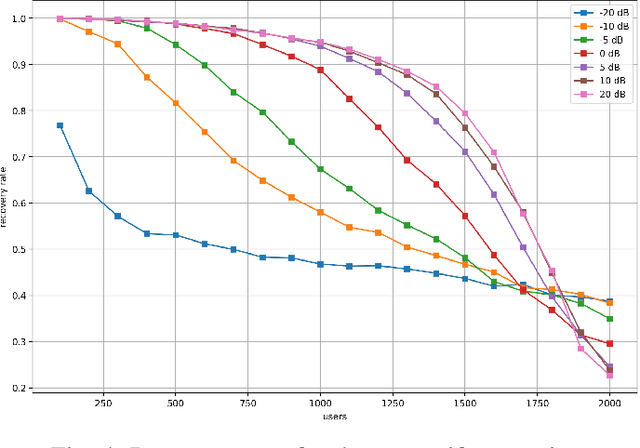
Compressive Sensing has well boosted massive random access protocols over the last decade. In this paper we apply an orthogonal FFT basis as it is used in OFDM, but subdivide its image into so-called sub-channels and let each sub-channel take only a fraction of the load. In a random fashion the subdivision is consecutively applied over a suitable number of time-slots. Within the time-slots the users will not change their sub-channel assignment and send in parallel the data. Activity detection is carried out jointly across time-slots in each of the sub-channels. For such system design we derive three rather fundamental results: i) First, we prove that the subdivision can be driven to the extent that the activity in each sub-channel is sparse by design. An effect that we call sparsity capture effect. ii) Second, we prove that effectively the system can sustain any overload situation relative to the FFT dimension, i.e. detection failure of active and non-active users can be kept below any desired threshold regardless of the number of users. The only price to pay is delay, i.e. the number of time-slots over which cross-detection is performed. We achieve this by jointly exploring the effect of measure concentration in time and frequency and careful system parameter scaling. iii) Third, we prove that parallel to activity detection active users can carry one symbol per pilot resource and time-slot so it supports so-called one-shot messaging. The key to proving these results are new concentration results for sequences of randomly sub-sampled FFTs detecting the sparse vectors "en bloc". Eventually, we show by simulations that the system is scalable resulting in a coarsely 30-fold capacity increase compared to standard OFDM.

A Reverse Jensen Inequality Result with Application to Mutual Information Estimation

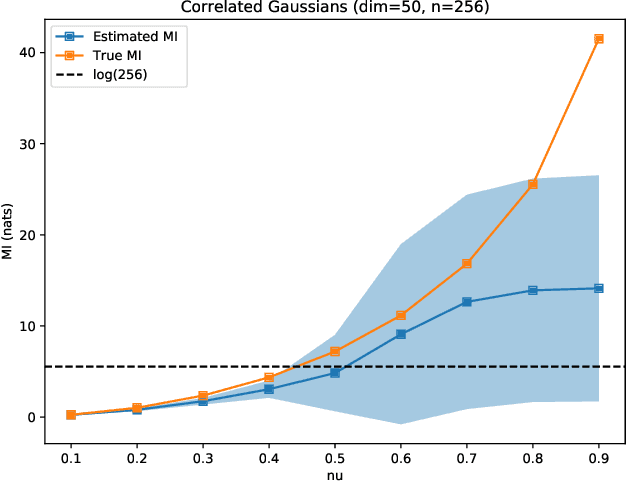
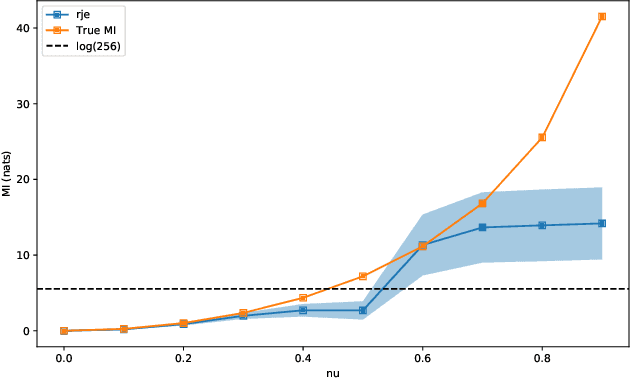
The Jensen inequality is a widely used tool in a multitude of fields, such as for example information theory and machine learning. It can be also used to derive other standard inequalities such as the inequality of arithmetic and geometric means or the H\"older inequality. In a probabilistic setting, the Jensen inequality describes the relationship between a convex function and the expected value. In this work, we want to look at the probabilistic setting from the reverse direction of the inequality. We show that under minimal constraints and with a proper scaling, the Jensen inequality can be reversed. We believe that the resulting tool can be helpful for many applications and provide a variational estimation of mutual information, where the reverse inequality leads to a new estimator with superior training behavior compared to current estimators.

Explicit CSI Feedback Compression via Learned Approximate Message Passing

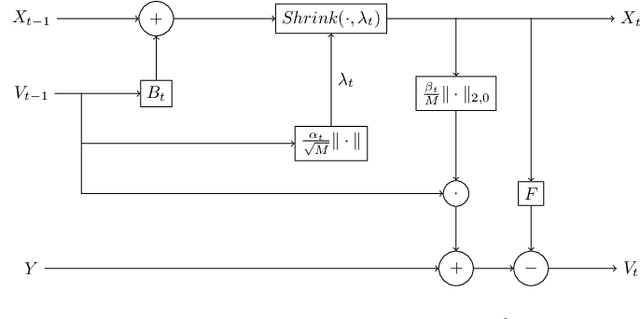
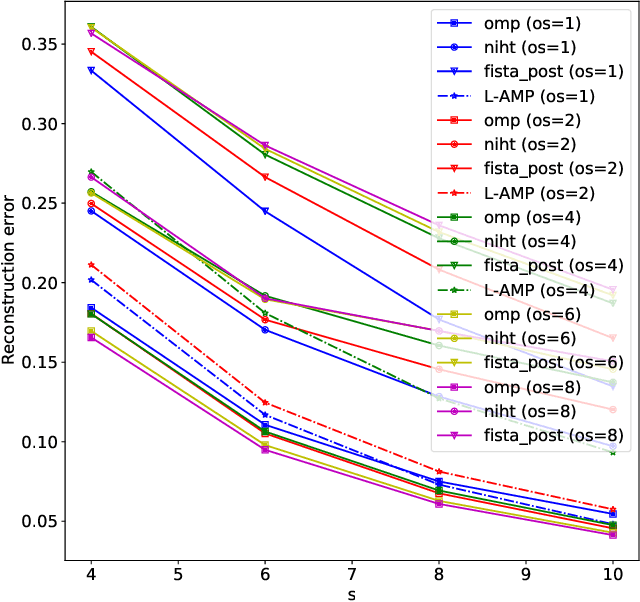
Explicit channel state information at the transmitter side is helpful to improve downlink precoding performance for multi-user MIMO systems. In order to reduce feedback signalling overhead, compression of Channel State Information (CSI) is essential. In this work different low complexity compressed sensing algorithms are compared in the context of an explicit CSI feedback scheme for 5G new radio. A neural network approach, based on learned approximate message passing for the computation of row-sparse solutions to matrix-valued compressed sensing problems is introduced. Due to extensive weight sharing, it shares the low memory footprint and fast evaluation of the forward pass with few iterations of a first order iterative algorithm. Furthermore it can be trained on purely synthetic data prior to deployment. Its performance in the explicit CSI feedback application is evaluated, and its key benefits in terms of computational complexity savings are discussed.

Measure Concentration on the OFDM-based Random Access Channel

It is well known that CS can boost massive random access protocols. Usually, the protocols operate in some overloaded regime where the sparsity can be exploited. In this paper, we consider a different approach by taking an orthogonal FFT base, subdivide its image into appropriate sub-channels and let each subchannel take only a fraction of the load. To show that this approach can actually achieve the full capacity we provide i) new concentration inequalities, and ii) devise a sparsity capture effect, i.e where the sub-division can be driven such that the activity in each each sub-channel is sparse by design. We show by simulations that the system is scalable resulting in a coarsely 30-fold capacity increase.

Hierarchical sparse recovery from hierarchically structured measurements with application to massive random access

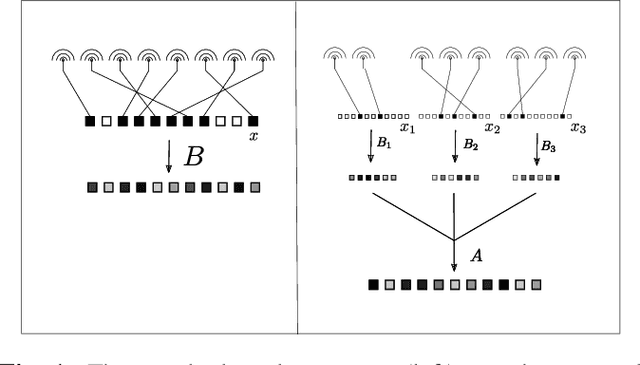
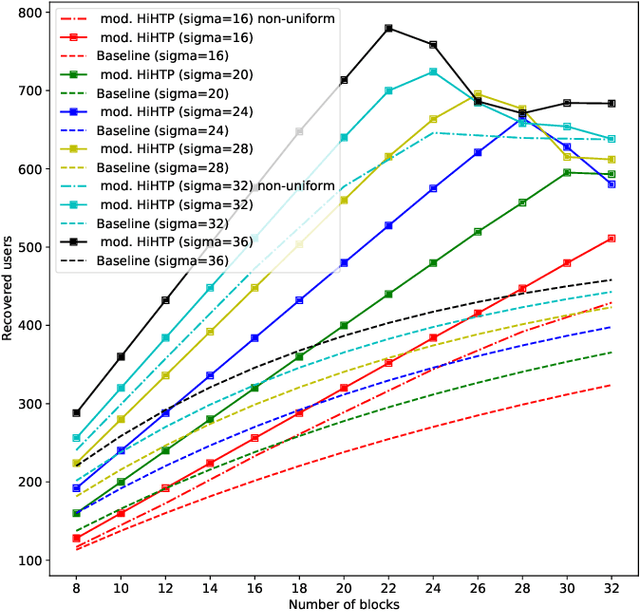
A new family of operators, coined hierarchical measurement operators, is introduced and discussed within the well-known hierarchical sparse recovery framework. Such operator is a composition of block and mixing operations and notably contains the Kronecker product as a special case. Results on their hierarchical restricted isometry property (HiRIP) are derived, generalizing prior work on recovery of hierarchically sparse signals from Kronecker-structured linear measurements. Specifically, these results show that, very surprisingly, sparsity properties of the block and mixing part can be traded against each other. The measurement structure is well-motivated by a massive random access channel design in communication engineering. Numerical evaluation of user detection rates demonstrate the huge benefit of the theoretical framework.

Hierarchical compressed sensing

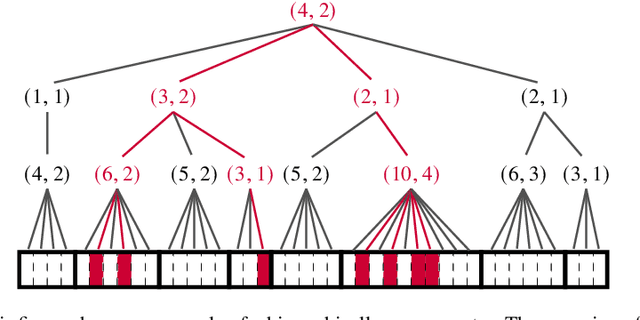
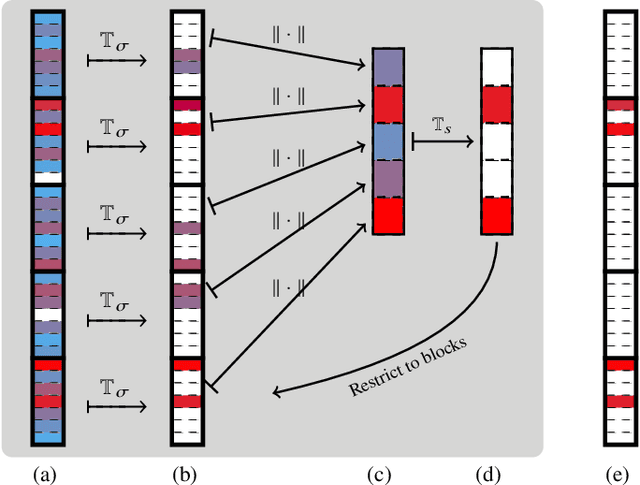
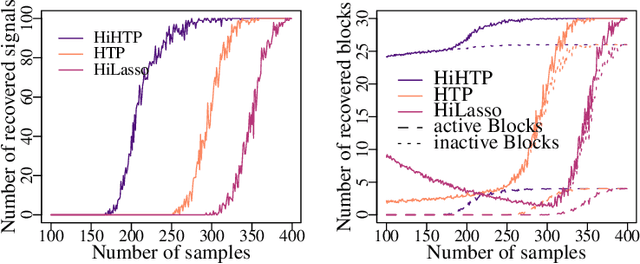
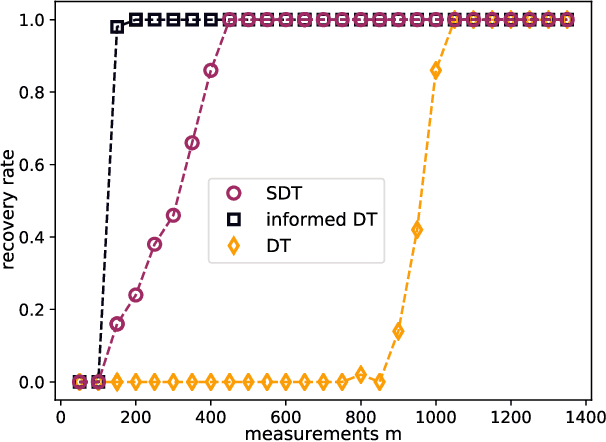
Compressed sensing is a paradigm within signal processing that provides the means for recovering structured signals from linear measurements in a highly efficient manner. Originally devised for the recovery of sparse signals, it has become clear that a similar methodology would also carry over to a wealth of other classes of structured signals. In this work, we provide an overview over the theory of compressed sensing for a particularly rich family of such signals, namely those of hierarchically structured signals. Examples of such signals are constituted by blocked vectors, with only few non-vanishing sparse blocks. We present recovery algorithms based on efficient hierarchical hard-thresholding. The algorithms are guaranteed to stable and robustly converge to the correct solution provide the measurement map acts isometrically restricted to the signal class. We then provide a series of results establishing that the required condition for large classes of measurement ensembles. Building upon this machinery, we sketch practical applications of this framework in machine-type and quantum communication.