Learning End-to-End Channel Coding with Diffusion Models

The training of neural encoders via deep learning necessitates a differentiable channel model due to the backpropagation algorithm. This requirement can be sidestepped by approximating either the channel distribution or its gradient through pilot signals in real-world scenarios. The initial approach draws upon the latest advancements in image generation, utilizing generative adversarial networks (GANs) or their enhanced variants to generate channel distributions. In this paper, we address this channel approximation challenge with diffusion models, which have demonstrated high sample quality in image generation. We offer an end-to-end channel coding framework underpinned by diffusion models and propose an efficient training algorithm. Our simulations with various channel models establish that our diffusion models learn the channel distribution accurately, thereby achieving near-optimal end-to-end symbol error rates (SERs). We also note a significant advantage of diffusion models: A robust generalization capability in high signal-to-noise ratio regions, in contrast to GAN variants that suffer from error floor. Furthermore, we examine the trade-off between sample quality and sampling speed, when an accelerated sampling algorithm is deployed, and investigate the effect of the noise scheduling on this trade-off. With an apt choice of noise scheduling, sampling time can be significantly reduced with a minor increase in SER.

Concatenated Classic and Neural (CCN) Codes: ConcatenatedAE

Small neural networks (NNs) used for error correction were shown to improve on classic channel codes and to address channel model changes. We extend the code dimension of any such structure by using the same NN under one-hot encoding multiple times, which are serially-concatenated with an outer classic code. We design NNs with the same network parameters, where each Reed-Solomon codeword symbol is an input to a different NN. Significant improvements in block error probabilities for an additive Gaussian noise channel as compared to the small neural code are illustrated, as well as robustness to channel model changes.

A Reverse Jensen Inequality Result with Application to Mutual Information Estimation

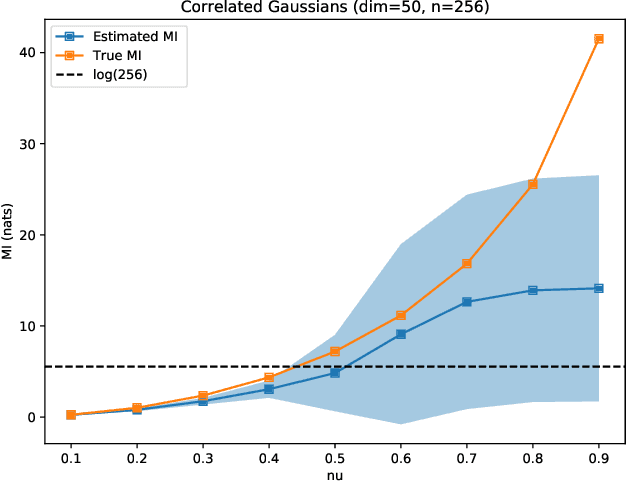
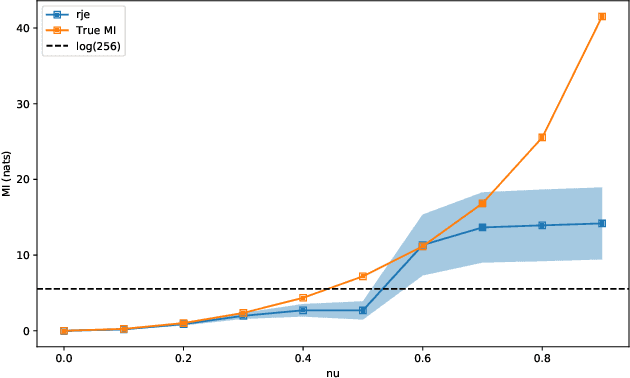
The Jensen inequality is a widely used tool in a multitude of fields, such as for example information theory and machine learning. It can be also used to derive other standard inequalities such as the inequality of arithmetic and geometric means or the H\"older inequality. In a probabilistic setting, the Jensen inequality describes the relationship between a convex function and the expected value. In this work, we want to look at the probabilistic setting from the reverse direction of the inequality. We show that under minimal constraints and with a proper scaling, the Jensen inequality can be reversed. We believe that the resulting tool can be helpful for many applications and provide a variational estimation of mutual information, where the reverse inequality leads to a new estimator with superior training behavior compared to current estimators.

Reinforce Security: A Model-Free Approach Towards Secure Wiretap Coding

The use of deep learning-based techniques for approximating secure encoding functions has attracted considerable interest in wireless communications due to impressive results obtained for general coding and decoding tasks for wireless communication systems. Of particular importance is the development of model-free techniques that work without knowledge about the underlying channel. Such techniques utilize for example generative adversarial networks to estimate and model the conditional channel distribution, mutual information estimation as a reward function, or reinforcement learning. In this paper, the approach of reinforcement learning is studied and, in particular, the policy gradient method for a model-free approach of neural network-based secure encoding is investigated. Previously developed techniques for enforcing a certain co-set structure on the encoding process can be combined with recent reinforcement learning approaches. This new approach is evaluated by extensive simulations, and it is demonstrated that the resulting decoding performance of an eavesdropper is capped at a certain error level.

Deep Learning for Channel Coding via Neural Mutual Information Estimation

End-to-end deep learning for communication systems, i.e., systems whose encoder and decoder are learned, has attracted significant interest recently, due to its performance which comes close to well-developed classical encoder-decoder designs. However, one of the drawbacks of current learning approaches is that a differentiable channel model is needed for the training of the underlying neural networks. In real-world scenarios, such a channel model is hardly available and often the channel density is not even known at all. Some works, therefore, focus on a generative approach, i.e., generating the channel from samples, or rely on reinforcement learning to circumvent this problem. We present a novel approach which utilizes a recently proposed neural estimator of mutual information. We use this estimator to optimize the encoder for a maximized mutual information, only relying on channel samples. Moreover, we show that our approach achieves the same performance as state-of-the-art end-to-end learning with perfect channel model knowledge.