Equivariant Manifold Neural ODEs and Differential Invariants

In this paper we develop a manifestly geometric framework for equivariant manifold neural ordinary differential equations (NODEs), and use it to analyse their modelling capabilities for symmetric data. First, we consider the action of a Lie group $G$ on a smooth manifold $M$ and establish the equivalence between equivariance of vector fields, symmetries of the corresponding Cauchy problems, and equivariance of the associated NODEs. We also propose a novel formulation of the equivariant NODEs in terms of the differential invariants of the action of $G$ on $M$, based on Lie theory for symmetries of differential equations, which provides an efficient parameterisation of the space of equivariant vector fields in a way that is agnostic to both the manifold $M$ and the symmetry group $G$. Second, we construct augmented manifold NODEs, through embeddings into equivariant flows, and show that they are universal approximators of equivariant diffeomorphisms on any path-connected $M$. Furthermore, we show that the augmented NODEs can be incorporated in the geometric framework and parameterised using higher order differential invariants. Finally, we consider the induced action of $G$ on different fields on $M$ and show how it can be used to generalise previous work, on, e.g., continuous normalizing flows, to equivariant models in any geometry.

HEAL-SWIN: A Vision Transformer On The Sphere

High-resolution wide-angle fisheye images are becoming more and more important for robotics applications such as autonomous driving. However, using ordinary convolutional neural networks or vision transformers on this data is problematic due to projection and distortion losses introduced when projecting to a rectangular grid on the plane. We introduce the HEAL-SWIN transformer, which combines the highly uniform Hierarchical Equal Area iso-Latitude Pixelation (HEALPix) grid used in astrophysics and cosmology with the Hierarchical Shifted-Window (SWIN) transformer to yield an efficient and flexible model capable of training on high-resolution, distortion-free spherical data. In HEAL-SWIN, the nested structure of the HEALPix grid is used to perform the patching and windowing operations of the SWIN transformer, resulting in a one-dimensional representation of the spherical data with minimal computational overhead. We demonstrate the superior performance of our model for semantic segmentation and depth regression tasks on both synthetic and real automotive datasets. Our code is available at https://github.com/JanEGerken/HEAL-SWIN.

Optimization Dynamics of Equivariant and Augmented Neural Networks

We investigate the optimization of multilayer perceptrons on symmetric data. We compare the strategy of constraining the architecture to be equivariant to that of using augmentation. We show that, under natural assumptions on the loss and non-linearities, the sets of equivariant stationary points are identical for the two strategies, and that the set of equivariant layers is invariant under the gradient flow for augmented models. Finally, we show that stationary points may be unstable for augmented training although they are stable for the equivariant models

Equivariance versus Augmentation for Spherical Images

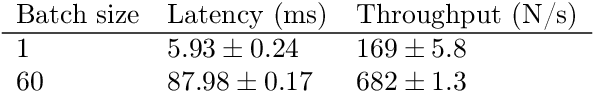
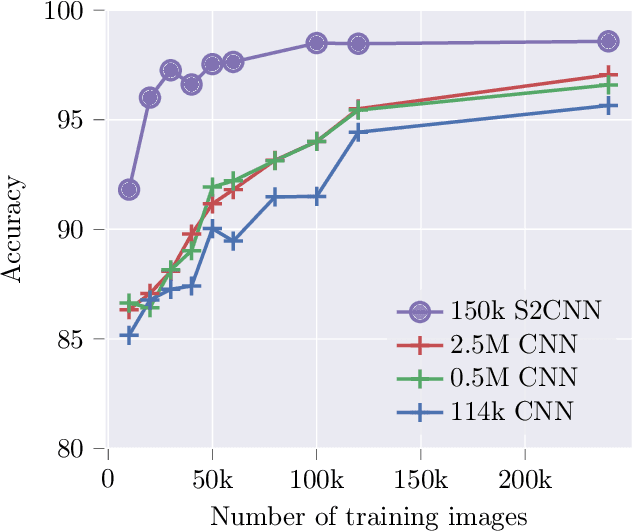
We analyze the role of rotational equivariance in convolutional neural networks (CNNs) applied to spherical images. We compare the performance of the group equivariant networks known as S2CNNs and standard non-equivariant CNNs trained with an increasing amount of data augmentation. The chosen architectures can be considered baseline references for the respective design paradigms. Our models are trained and evaluated on single or multiple items from the MNIST or FashionMNIST dataset projected onto the sphere. For the task of image classification, which is inherently rotationally invariant, we find that by considerably increasing the amount of data augmentation and the size of the networks, it is possible for the standard CNNs to reach at least the same performance as the equivariant network. In contrast, for the inherently equivariant task of semantic segmentation, the non-equivariant networks are consistently outperformed by the equivariant networks with significantly fewer parameters. We also analyze and compare the inference latency and training times of the different networks, enabling detailed tradeoff considerations between equivariant architectures and data augmentation for practical problems. The equivariant spherical networks used in the experiments will be made available at https://github.com/JanEGerken/sem_seg_s2cnn .

Geometric Deep Learning and Equivariant Neural Networks

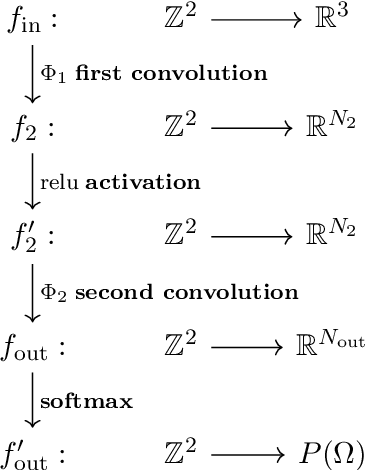
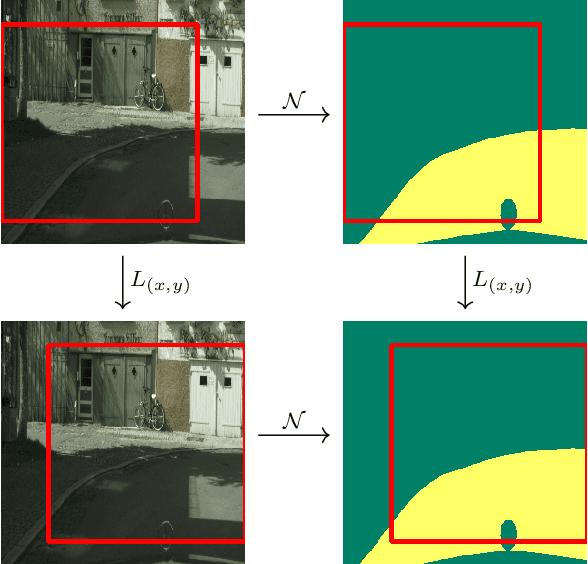
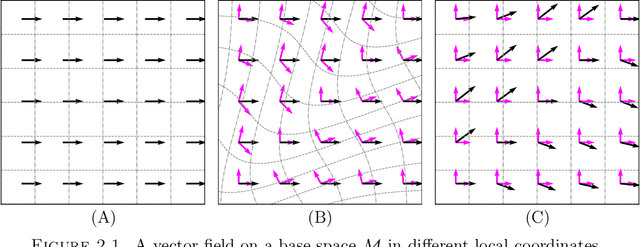
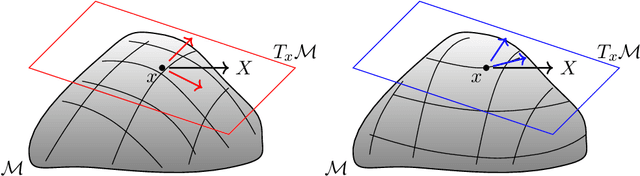
We survey the mathematical foundations of geometric deep learning, focusing on group equivariant and gauge equivariant neural networks. We develop gauge equivariant convolutional neural networks on arbitrary manifolds $\mathcal{M}$ using principal bundles with structure group $K$ and equivariant maps between sections of associated vector bundles. We also discuss group equivariant neural networks for homogeneous spaces $\mathcal{M}=G/K$, which are instead equivariant with respect to the global symmetry $G$ on $\mathcal{M}$. Group equivariant layers can be interpreted as intertwiners between induced representations of $G$, and we show their relation to gauge equivariant convolutional layers. We analyze several applications of this formalism, including semantic segmentation and object detection networks. We also discuss the case of spherical networks in great detail, corresponding to the case $\mathcal{M}=S^2=\mathrm{SO}(3)/\mathrm{SO}(2)$. Here we emphasize the use of Fourier analysis involving Wigner matrices, spherical harmonics and Clebsch-Gordan coefficients for $G=\mathrm{SO}(3)$, illustrating the power of representation theory for deep learning.