Bayesian Predictive Coding

Predictive coding (PC) is an influential theory of information processing in the brain, providing a biologically plausible alternative to backpropagation. It is motivated in terms of Bayesian inference, as hidden states and parameters are optimised via gradient descent on variational free energy. However, implementations of PC rely on maximum \textit{a posteriori} (MAP) estimates of hidden states and maximum likelihood (ML) estimates of parameters, limiting their ability to quantify epistemic uncertainty. In this work, we investigate a Bayesian extension to PC that estimates a posterior distribution over network parameters. This approach, termed Bayesian Predictive coding (BPC), preserves the locality of PC and results in closed-form Hebbian weight updates. Compared to PC, our BPC algorithm converges in fewer epochs in the full-batch setting and remains competitive in the mini-batch setting. Additionally, we demonstrate that BPC offers uncertainty quantification comparable to existing methods in Bayesian deep learning, while also improving convergence properties. Together, these results suggest that BPC provides a biologically plausible method for Bayesian learning in the brain, as well as an attractive approach to uncertainty quantification in deep learning.

Learning Chern Numbers of Topological Insulators with Gauge Equivariant Neural Networks

Equivariant network architectures are a well-established tool for predicting invariant or equivariant quantities. However, almost all learning problems considered in this context feature a global symmetry, i.e. each point of the underlying space is transformed with the same group element, as opposed to a local ``gauge'' symmetry, where each point is transformed with a different group element, exponentially enlarging the size of the symmetry group. Gauge equivariant networks have so far mainly been applied to problems in quantum chromodynamics. Here, we introduce a novel application domain for gauge-equivariant networks in the theory of topological condensed matter physics. We use gauge equivariant networks to predict topological invariants (Chern numbers) of multiband topological insulators. The gauge symmetry of the network guarantees that the predicted quantity is a topological invariant. We introduce a novel gauge equivariant normalization layer to stabilize the training and prove a universal approximation theorem for our setup. We train on samples with trivial Chern number only but show that our models generalize to samples with non-trivial Chern number. We provide various ablations of our setup. Our code is available at https://github.com/sitronsea/GENet/tree/main.

Uncertainty quantification in fine-tuned LLMs using LoRA ensembles

Fine-tuning large language models can improve task specific performance, although a general understanding of what the fine-tuned model has learned, forgotten and how to trust its predictions is still missing. We derive principled uncertainty quantification for fine-tuned LLMs with posterior approximations using computationally efficient low-rank adaptation ensembles. We analyze three common multiple-choice datasets using low-rank adaptation ensembles based on Mistral-7b, and draw quantitative and qualitative conclusions on their perceived complexity and model efficacy on the different target domains during and after fine-tuning. In particular, backed by the numerical experiments, we hypothesise about signals from entropic uncertainty measures for data domains that are inherently difficult for a given architecture to learn.

HEAL-SWIN: A Vision Transformer On The Sphere

High-resolution wide-angle fisheye images are becoming more and more important for robotics applications such as autonomous driving. However, using ordinary convolutional neural networks or vision transformers on this data is problematic due to projection and distortion losses introduced when projecting to a rectangular grid on the plane. We introduce the HEAL-SWIN transformer, which combines the highly uniform Hierarchical Equal Area iso-Latitude Pixelation (HEALPix) grid used in astrophysics and cosmology with the Hierarchical Shifted-Window (SWIN) transformer to yield an efficient and flexible model capable of training on high-resolution, distortion-free spherical data. In HEAL-SWIN, the nested structure of the HEALPix grid is used to perform the patching and windowing operations of the SWIN transformer, resulting in a one-dimensional representation of the spherical data with minimal computational overhead. We demonstrate the superior performance of our model for semantic segmentation and depth regression tasks on both synthetic and real automotive datasets. Our code is available at https://github.com/JanEGerken/HEAL-SWIN.

Bayesian posterior approximation with stochastic ensembles

We introduce ensembles of stochastic neural networks to approximate the Bayesian posterior, combining stochastic methods such as dropout with deep ensembles. The stochastic ensembles are formulated as families of distributions and trained to approximate the Bayesian posterior with variational inference. We implement stochastic ensembles based on Monte Carlo dropout, DropConnect and a novel non-parametric version of dropout and evaluate them on a toy problem and CIFAR image classification. For CIFAR, the stochastic ensembles are quantitatively compared to published Hamiltonian Monte Carlo results for a ResNet-20 architecture. We also test the quality of the posteriors directly against Hamiltonian Monte Carlo simulations in a simplified toy model. Our results show that in a number of settings, stochastic ensembles provide more accurate posterior estimates than regular deep ensembles.

Real-time semantic segmentation on FPGAs for autonomous vehicles with hls4ml

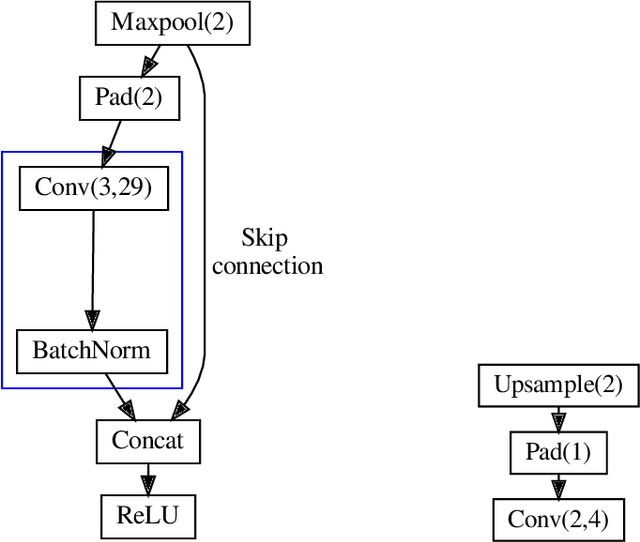
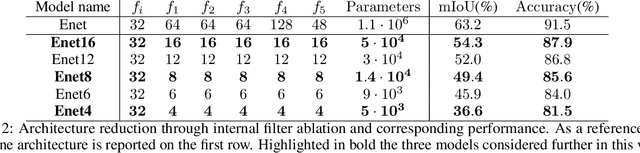
In this paper, we investigate how field programmable gate arrays can serve as hardware accelerators for real-time semantic segmentation tasks relevant for autonomous driving. Considering compressed versions of the ENet convolutional neural network architecture, we demonstrate a fully-on-chip deployment with a latency of 4.9 ms per image, using less than 30% of the available resources on a Xilinx ZCU102 evaluation board. The latency is reduced to 3 ms per image when increasing the batch size to ten, corresponding to the use case where the autonomous vehicle receives inputs from multiple cameras simultaneously. We show, through aggressive filter reduction and heterogeneous quantization-aware training, and an optimized implementation of convolutional layers, that the power consumption and resource utilization can be significantly reduced while maintaining accuracy on the Cityscapes dataset.

Equivariance versus Augmentation for Spherical Images

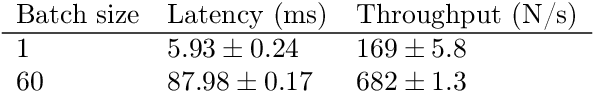
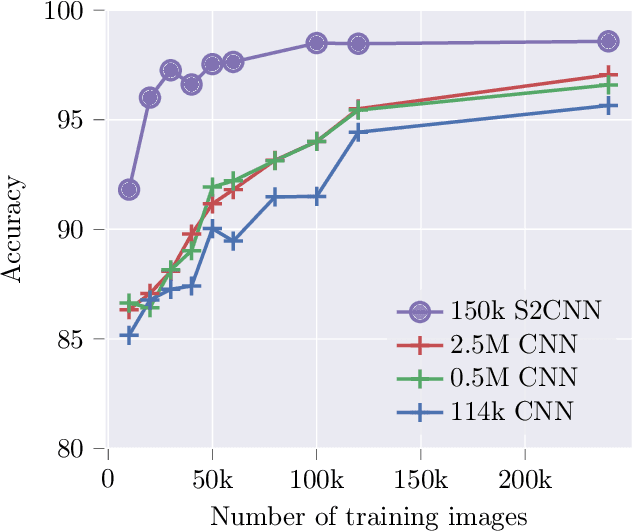
We analyze the role of rotational equivariance in convolutional neural networks (CNNs) applied to spherical images. We compare the performance of the group equivariant networks known as S2CNNs and standard non-equivariant CNNs trained with an increasing amount of data augmentation. The chosen architectures can be considered baseline references for the respective design paradigms. Our models are trained and evaluated on single or multiple items from the MNIST or FashionMNIST dataset projected onto the sphere. For the task of image classification, which is inherently rotationally invariant, we find that by considerably increasing the amount of data augmentation and the size of the networks, it is possible for the standard CNNs to reach at least the same performance as the equivariant network. In contrast, for the inherently equivariant task of semantic segmentation, the non-equivariant networks are consistently outperformed by the equivariant networks with significantly fewer parameters. We also analyze and compare the inference latency and training times of the different networks, enabling detailed tradeoff considerations between equivariant architectures and data augmentation for practical problems. The equivariant spherical networks used in the experiments will be made available at https://github.com/JanEGerken/sem_seg_s2cnn .

Geometric Deep Learning and Equivariant Neural Networks

We survey the mathematical foundations of geometric deep learning, focusing on group equivariant and gauge equivariant neural networks. We develop gauge equivariant convolutional neural networks on arbitrary manifolds $\mathcal{M}$ using principal bundles with structure group $K$ and equivariant maps between sections of associated vector bundles. We also discuss group equivariant neural networks for homogeneous spaces $\mathcal{M}=G/K$, which are instead equivariant with respect to the global symmetry $G$ on $\mathcal{M}$. Group equivariant layers can be interpreted as intertwiners between induced representations of $G$, and we show their relation to gauge equivariant convolutional layers. We analyze several applications of this formalism, including semantic segmentation and object detection networks. We also discuss the case of spherical networks in great detail, corresponding to the case $\mathcal{M}=S^2=\mathrm{SO}(3)/\mathrm{SO}(2)$. Here we emphasize the use of Fourier analysis involving Wigner matrices, spherical harmonics and Clebsch-Gordan coefficients for $G=\mathrm{SO}(3)$, illustrating the power of representation theory for deep learning.

Fast convolutional neural networks on FPGAs with hls4ml

We introduce an automated tool for deploying ultra low-latency, low-power deep neural networks with large convolutional layers on FPGAs. By extending the hls4ml library, we demonstrate how to achieve inference latency of $5\,\mu$s using convolutional architectures, while preserving state-of-the-art model performance. Considering benchmark models trained on the Street View House Numbers Dataset, we demonstrate various methods for model compression in order to fit the computational constraints of a typical FPGA device. In particular, we discuss pruning and quantization-aware training, and demonstrate how resource utilization can be reduced by over 90% while maintaining the original model accuracy.