Navigation under uncertainty: Trajectory prediction and occlusion reasoning with switching dynamical systems

Predicting future trajectories of nearby objects, especially under occlusion, is a crucial task in autonomous driving and safe robot navigation. Prior works typically neglect to maintain uncertainty about occluded objects and only predict trajectories of observed objects using high-capacity models such as Transformers trained on large datasets. While these approaches are effective in standard scenarios, they can struggle to generalize to the long-tail, safety-critical scenarios. In this work, we explore a conceptual framework unifying trajectory prediction and occlusion reasoning under the same class of structured probabilistic generative model, namely, switching dynamical systems. We then present some initial experiments illustrating its capabilities using the Waymo open dataset.

Gradient-free variational learning with conditional mixture networks

Balancing computational efficiency with robust predictive performance is crucial in supervised learning, especially for critical applications. Standard deep learning models, while accurate and scalable, often lack probabilistic features like calibrated predictions and uncertainty quantification. Bayesian methods address these issues but can be computationally expensive as model and data complexity increase. Previous work shows that fast variational methods can reduce the compute requirements of Bayesian methods by eliminating the need for gradient computation or sampling, but are often limited to simple models. We demonstrate that conditional mixture networks (CMNs), a probabilistic variant of the mixture-of-experts (MoE) model, are suitable for fast, gradient-free inference and can solve complex classification tasks. CMNs employ linear experts and a softmax gating network. By exploiting conditional conjugacy and P\'olya-Gamma augmentation, we furnish Gaussian likelihoods for the weights of both the linear experts and the gating network. This enables efficient variational updates using coordinate ascent variational inference (CAVI), avoiding traditional gradient-based optimization. We validate this approach by training two-layer CMNs on standard benchmarks from the UCI repository. Our method, CAVI-CMN, achieves competitive and often superior predictive accuracy compared to maximum likelihood estimation (MLE) with backpropagation, while maintaining competitive runtime and full posterior distributions over all model parameters. Moreover, as input size or the number of experts increases, computation time scales competitively with MLE and other gradient-based solutions like black-box variational inference (BBVI), making CAVI-CMN a promising tool for deep, fast, and gradient-free Bayesian networks.

From pixels to planning: scale-free active inference

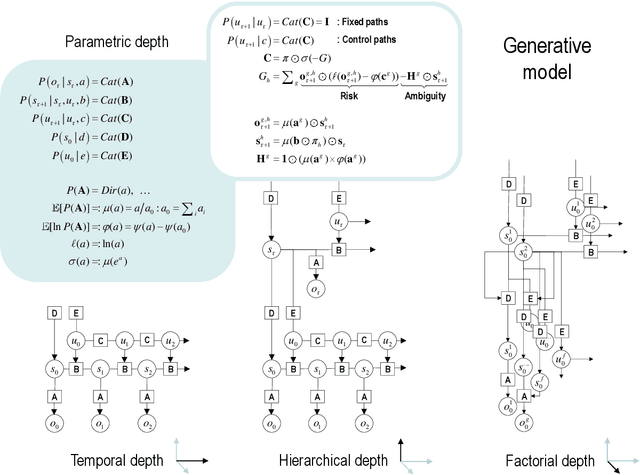
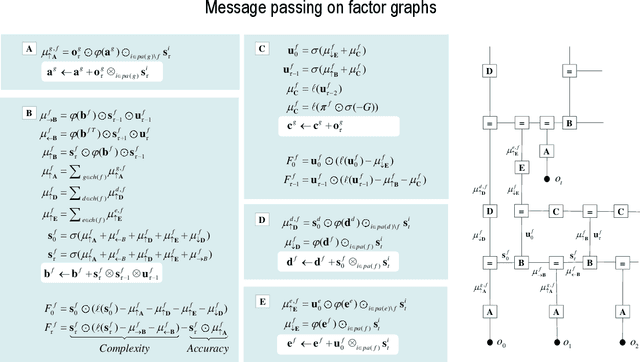
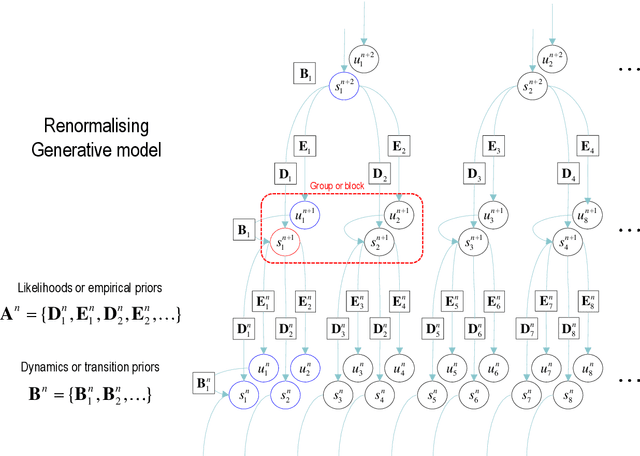
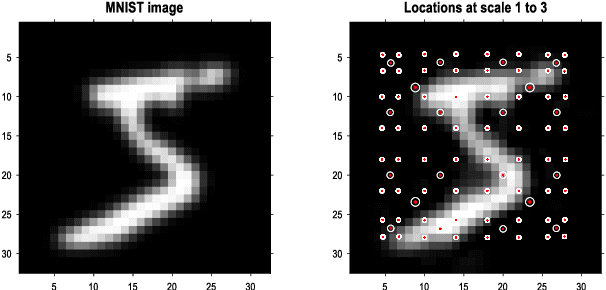
This paper describes a discrete state-space model -- and accompanying methods -- for generative modelling. This model generalises partially observed Markov decision processes to include paths as latent variables, rendering it suitable for active inference and learning in a dynamic setting. Specifically, we consider deep or hierarchical forms using the renormalisation group. The ensuing renormalising generative models (RGM) can be regarded as discrete homologues of deep convolutional neural networks or continuous state-space models in generalised coordinates of motion. By construction, these scale-invariant models can be used to learn compositionality over space and time, furnishing models of paths or orbits; i.e., events of increasing temporal depth and itinerancy. This technical note illustrates the automatic discovery, learning and deployment of RGMs using a series of applications. We start with image classification and then consider the compression and generation of movies and music. Finally, we apply the same variational principles to the learning of Atari-like games.

Understanding the origin of information-seeking exploration in probabilistic objectives for control

The exploration-exploitation trade-off is central to the description of adaptive behaviour in fields ranging from machine learning, to biology, to economics. While many approaches have been taken, one approach to solving this trade-off has been to equip or propose that agents possess an intrinsic 'exploratory drive' which is often implemented in terms of maximizing the agents information gain about the world -- an approach which has been widely studied in machine learning and cognitive science. In this paper we mathematically investigate the nature and meaning of such approaches and demonstrate that this combination of utility maximizing and information-seeking behaviour arises from the minimization of an entirely difference class of objectives we call divergence objectives. We propose a dichotomy in the objective functions underlying adaptive behaviour between \emph{evidence} objectives, which correspond to well-known reward or utility maximizing objectives in the literature, and \emph{divergence} objectives which instead seek to minimize the divergence between the agent's expected and desired futures, and argue that this new class of divergence objectives could form the mathematical foundation for a much richer understanding of the exploratory components of adaptive and intelligent action, beyond simply greedy utility maximization.

Neural Kalman Filtering

The Kalman filter is a fundamental filtering algorithm that fuses noisy sensory data, a previous state estimate, and a dynamics model to produce a principled estimate of the current state. It assumes, and is optimal for, linear models and white Gaussian noise. Due to its relative simplicity and general effectiveness, the Kalman filter is widely used in engineering applications. Since many sensory problems the brain faces are, at their core, filtering problems, it is possible that the brain possesses neural circuitry that implements equivalent computations to the Kalman filter. The standard approach to Kalman filtering requires complex matrix computations that are unlikely to be directly implementable in neural circuits. In this paper, we show that a gradient-descent approximation to the Kalman filter requires only local computations with variance weighted prediction errors. Moreover, we show that it is possible under the same scheme to adaptively learn the dynamics model with a learning rule that corresponds directly to Hebbian plasticity. We demonstrate the performance of our method on a simple Kalman filtering task, and propose a neural implementation of the required equations.