A Mathematical Walkthrough and Discussion of the Free Energy Principle

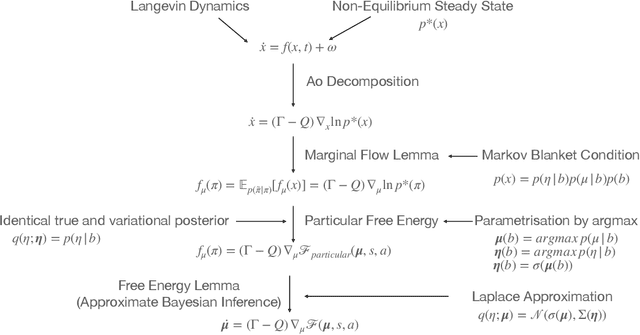
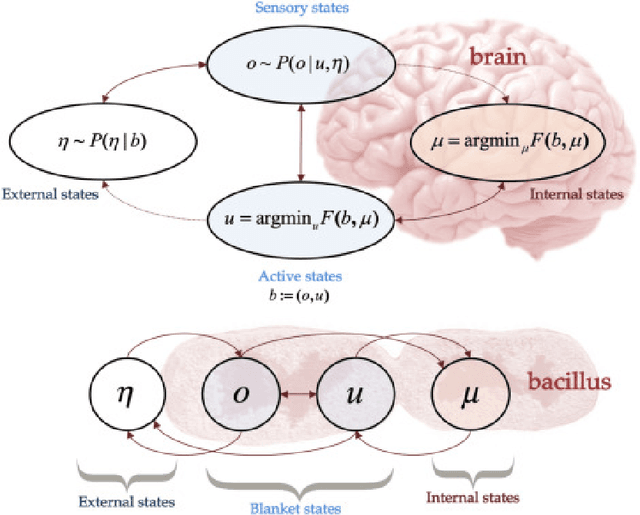
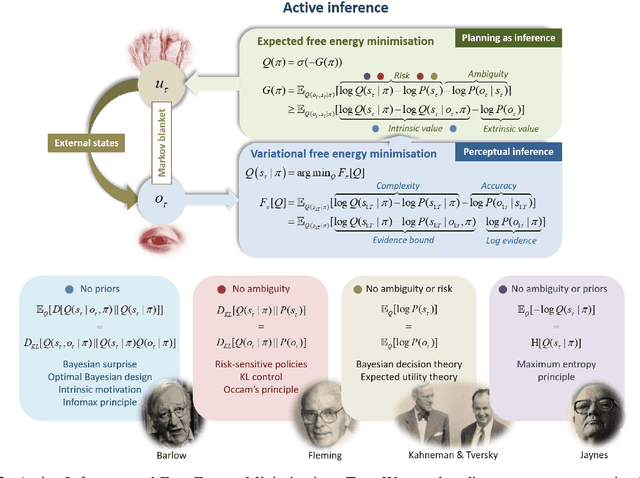
The Free-Energy-Principle (FEP) is an influential and controversial theory which postulates a deep and powerful connection between the stochastic thermodynamics of self-organization and learning through variational inference. Specifically, it claims that any self-organizing system which can be statistically separated from its environment, and which maintains itself at a non-equilibrium steady state, can be construed as minimizing an information-theoretic functional -- the variational free energy -- and thus performing variational Bayesian inference to infer the hidden state of its environment. This principle has also been applied extensively in neuroscience, and is beginning to make inroads in machine learning by spurring the construction of novel and powerful algorithms by which action, perception, and learning can all be unified under a single objective. While its expansive and often grandiose claims have spurred significant debates in both philosophy and theoretical neuroscience, the mathematical depth and lack of accessible introductions and tutorials for the core claims of the theory have often precluded a deep understanding within the literature. Here, we aim to provide a mathematically detailed, yet intuitive walk-through of the formulation and central claims of the FEP while also providing a discussion of the assumptions necessary and potential limitations of the theory. Additionally, since the FEP is a still a living theory, subject to internal controversy, change, and revision, we also present a detailed appendix highlighting and condensing current perspectives as well as controversies about the nature, applicability, and the mathematical assumptions and formalisms underlying the FEP.

Predictive Coding: a Theoretical and Experimental Review

Predictive coding offers a potentially unifying account of cortical function -- postulating that the core function of the brain is to minimize prediction errors with respect to a generative model of the world. The theory is closely related to the Bayesian brain framework and, over the last two decades, has gained substantial influence in the fields of theoretical and cognitive neuroscience. A large body of research has arisen based on both empirically testing improved and extended theoretical and mathematical models of predictive coding, as well as in evaluating their potential biological plausibility for implementation in the brain and the concrete neurophysiological and psychological predictions made by the theory. Despite this enduring popularity, however, no comprehensive review of predictive coding theory, and especially of recent developments in this field, exists. Here, we provide a comprehensive review both of the core mathematical structure and logic of predictive coding, thus complementing recent tutorials in the literature. We also review a wide range of classic and recent work within the framework, ranging from the neurobiologically realistic microcircuits that could implement predictive coding, to the close relationship between predictive coding and the widely-used backpropagation of error algorithm, as well as surveying the close relationships between predictive coding and modern machine learning techniques.

Understanding the origin of information-seeking exploration in probabilistic objectives for control

The exploration-exploitation trade-off is central to the description of adaptive behaviour in fields ranging from machine learning, to biology, to economics. While many approaches have been taken, one approach to solving this trade-off has been to equip or propose that agents possess an intrinsic 'exploratory drive' which is often implemented in terms of maximizing the agents information gain about the world -- an approach which has been widely studied in machine learning and cognitive science. In this paper we mathematically investigate the nature and meaning of such approaches and demonstrate that this combination of utility maximizing and information-seeking behaviour arises from the minimization of an entirely difference class of objectives we call divergence objectives. We propose a dichotomy in the objective functions underlying adaptive behaviour between \emph{evidence} objectives, which correspond to well-known reward or utility maximizing objectives in the literature, and \emph{divergence} objectives which instead seek to minimize the divergence between the agent's expected and desired futures, and argue that this new class of divergence objectives could form the mathematical foundation for a much richer understanding of the exploratory components of adaptive and intelligent action, beyond simply greedy utility maximization.

Neural Kalman Filtering

The Kalman filter is a fundamental filtering algorithm that fuses noisy sensory data, a previous state estimate, and a dynamics model to produce a principled estimate of the current state. It assumes, and is optimal for, linear models and white Gaussian noise. Due to its relative simplicity and general effectiveness, the Kalman filter is widely used in engineering applications. Since many sensory problems the brain faces are, at their core, filtering problems, it is possible that the brain possesses neural circuitry that implements equivalent computations to the Kalman filter. The standard approach to Kalman filtering requires complex matrix computations that are unlikely to be directly implementable in neural circuits. In this paper, we show that a gradient-descent approximation to the Kalman filter requires only local computations with variance weighted prediction errors. Moreover, we show that it is possible under the same scheme to adaptively learn the dynamics model with a learning rule that corresponds directly to Hebbian plasticity. We demonstrate the performance of our method on a simple Kalman filtering task, and propose a neural implementation of the required equations.

Investigating the Scalability and Biological Plausibility of the Activation Relaxation Algorithm

The recently proposed Activation Relaxation (AR) algorithm provides a simple and robust approach for approximating the backpropagation of error algorithm using only local learning rules. Unlike competing schemes, it converges to the exact backpropagation gradients, and utilises only a single type of computational unit and a single backwards relaxation phase. We have previously shown that the algorithm can be further simplified and made more biologically plausible by (i) introducing a learnable set of backwards weights, which overcomes the weight-transport problem, and (ii) avoiding the computation of nonlinear derivatives at each neuron. However, tthe efficacy of these simplifications has, so far, only been tested on simple multi-layer-perceptron (MLP) networks. Here, we show that these simplifications still maintain performance using more complex CNN architectures and challenging datasets, which have proven difficult for other biologically-plausible schemes to scale to. We also investigate whether another biologically implausible assumption of the original AR algorithm -- the frozen feedforward pass -- can be relaxed without damaging performance.

Relaxing the Constraints on Predictive Coding Models

Predictive coding is an influential theory of cortical function which posits that the principal computation the brain performs, which underlies both perception and learning, is the minimization of prediction errors. While motivated by high-level notions of variational inference, detailed neurophysiological models of cortical microcircuits which can implements its computations have been developed. Moreover, under certain conditions, predictive coding has been shown to approximate the backpropagation of error algorithm, and thus provides a relatively biologically plausible credit-assignment mechanism for training deep networks. However, standard implementations of the algorithm still involve potentially neurally implausible features such as identical forward and backward weights, backward nonlinear derivatives, and 1-1 error unit connectivity. In this paper, we show that these features are not integral to the algorithm and can be removed either directly or through learning additional sets of parameters with Hebbian update rules without noticeable harm to learning performance. Our work thus relaxes current constraints on potential microcircuit designs and hopefully opens up new regions of the design-space for neuromorphic implementations of predictive coding.