A Mathematical Walkthrough and Discussion of the Free Energy Principle
Paper and Code
Aug 30, 2021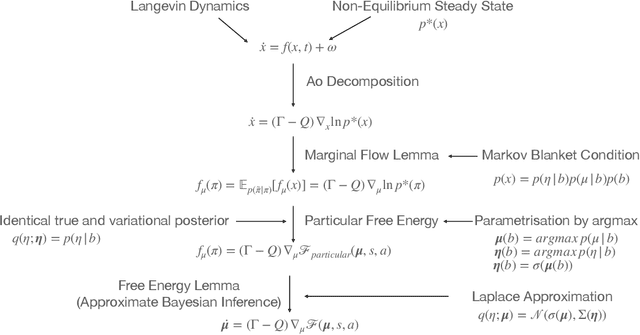
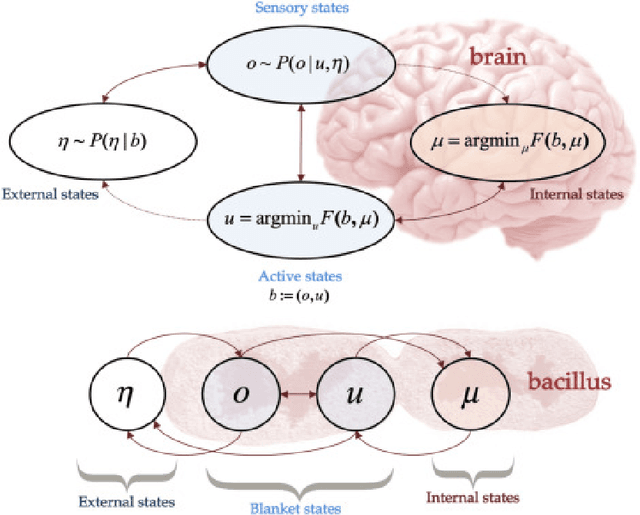
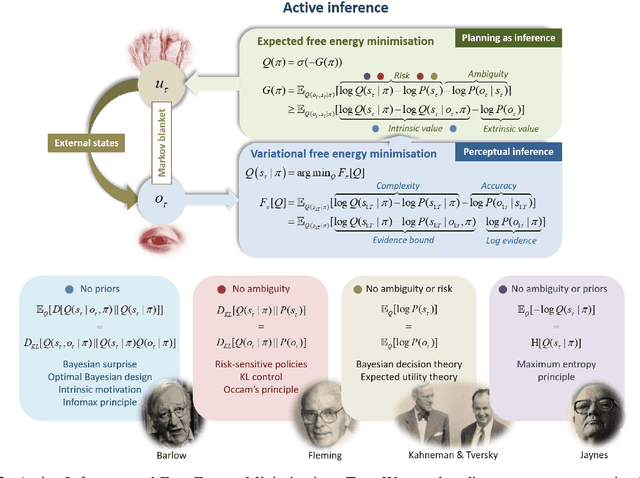
The Free-Energy-Principle (FEP) is an influential and controversial theory which postulates a deep and powerful connection between the stochastic thermodynamics of self-organization and learning through variational inference. Specifically, it claims that any self-organizing system which can be statistically separated from its environment, and which maintains itself at a non-equilibrium steady state, can be construed as minimizing an information-theoretic functional -- the variational free energy -- and thus performing variational Bayesian inference to infer the hidden state of its environment. This principle has also been applied extensively in neuroscience, and is beginning to make inroads in machine learning by spurring the construction of novel and powerful algorithms by which action, perception, and learning can all be unified under a single objective. While its expansive and often grandiose claims have spurred significant debates in both philosophy and theoretical neuroscience, the mathematical depth and lack of accessible introductions and tutorials for the core claims of the theory have often precluded a deep understanding within the literature. Here, we aim to provide a mathematically detailed, yet intuitive walk-through of the formulation and central claims of the FEP while also providing a discussion of the assumptions necessary and potential limitations of the theory. Additionally, since the FEP is a still a living theory, subject to internal controversy, change, and revision, we also present a detailed appendix highlighting and condensing current perspectives as well as controversies about the nature, applicability, and the mathematical assumptions and formalisms underlying the FEP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge