Learning in Hybrid Active Inference Models

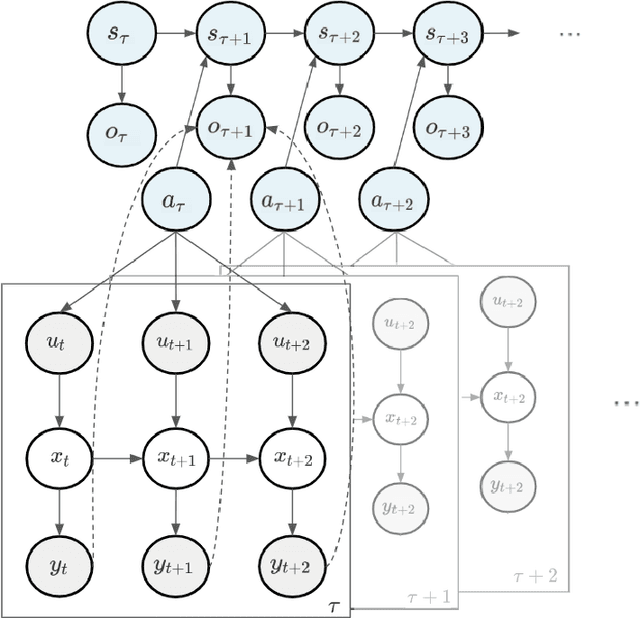
An open problem in artificial intelligence is how systems can flexibly learn discrete abstractions that are useful for solving inherently continuous problems. Previous work in computational neuroscience has considered this functional integration of discrete and continuous variables during decision-making under the formalism of active inference (Parr, Friston & de Vries, 2017; Parr & Friston, 2018). However, their focus is on the expressive physical implementation of categorical decisions and the hierarchical mixed generative model is assumed to be known. As a consequence, it is unclear how this framework might be extended to learning. We therefore present a novel hierarchical hybrid active inference agent in which a high-level discrete active inference planner sits above a low-level continuous active inference controller. We make use of recent work in recurrent switching linear dynamical systems (rSLDS) which implement end-to-end learning of meaningful discrete representations via the piecewise linear decomposition of complex continuous dynamics (Linderman et al., 2016). The representations learned by the rSLDS inform the structure of the hybrid decision-making agent and allow us to (1) specify temporally-abstracted sub-goals in a method reminiscent of the options framework, (2) lift the exploration into discrete space allowing us to exploit information-theoretic exploration bonuses and (3) `cache' the approximate solutions to low-level problems in the discrete planner. We apply our model to the sparse Continuous Mountain Car task, demonstrating fast system identification via enhanced exploration and successful planning through the delineation of abstract sub-goals.

Hybrid Recurrent Models Support Emergent Descriptions for Hierarchical Planning and Control

An open problem in artificial intelligence is how systems can flexibly learn discrete abstractions that are useful for solving inherently continuous problems. Previous work has demonstrated that a class of hybrid state-space model known as recurrent switching linear dynamical systems (rSLDS) discover meaningful behavioural units via the piecewise linear decomposition of complex continuous dynamics (Linderman et al., 2016). Furthermore, they model how the underlying continuous states drive these discrete mode switches. We propose that the rich representations formed by an rSLDS can provide useful abstractions for planning and control. We present a novel hierarchical model-based algorithm inspired by Active Inference in which a discrete MDP sits above a low-level linear-quadratic controller. The recurrent transition dynamics learned by the rSLDS allow us to (1) specify temporally-abstracted sub-goals in a method reminiscent of the options framework, (2) lift the exploration into discrete space allowing us to exploit information-theoretic exploration bonuses and (3) `cache' the approximate solutions to low-level problems in the discrete planner. We successfully apply our model to the sparse Continuous Mountain Car task, demonstrating fast system identification via enhanced exploration and non-trivial planning through the delineation of abstract sub-goals.

Supervised structure learning

This paper concerns structure learning or discovery of discrete generative models. It focuses on Bayesian model selection and the assimilation of training data or content, with a special emphasis on the order in which data are ingested. A key move - in the ensuing schemes - is to place priors on the selection of models, based upon expected free energy. In this setting, expected free energy reduces to a constrained mutual information, where the constraints inherit from priors over outcomes (i.e., preferred outcomes). The resulting scheme is first used to perform image classification on the MNIST dataset to illustrate the basic idea, and then tested on a more challenging problem of discovering models with dynamics, using a simple sprite-based visual disentanglement paradigm and the Tower of Hanoi (cf., blocks world) problem. In these examples, generative models are constructed autodidactically to recover (i.e., disentangle) the factorial structure of latent states - and their characteristic paths or dynamics.

Understanding Tool Discovery and Tool Innovation Using Active Inference

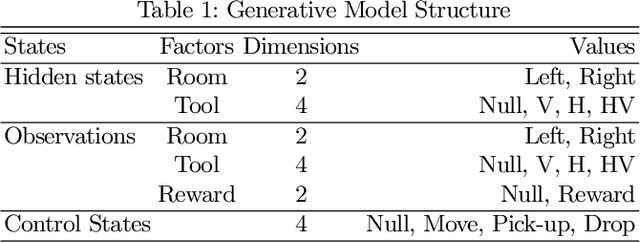
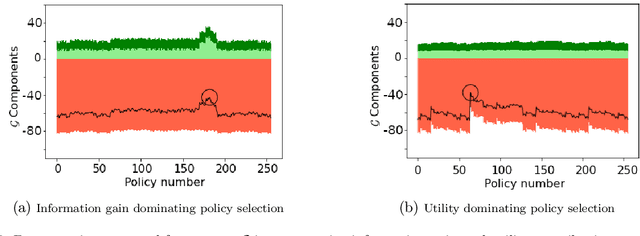
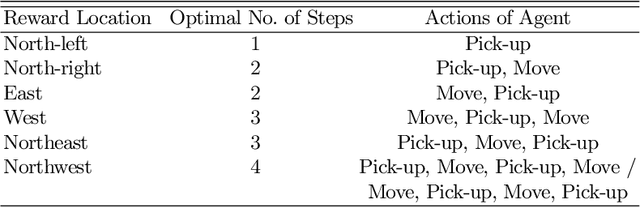
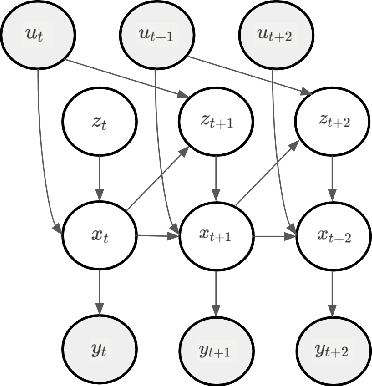
The ability to invent new tools has been identified as an important facet of our ability as a species to problem solve in dynamic and novel environments. While the use of tools by artificial agents presents a challenging task and has been widely identified as a key goal in the field of autonomous robotics, far less research has tackled the invention of new tools by agents. In this paper, (1) we articulate the distinction between tool discovery and tool innovation by providing a minimal description of the two concepts under the formalism of active inference. We then (2) apply this description to construct a toy model of tool innovation by introducing the notion of tool affordances into the hidden states of the agent's probabilistic generative model. This particular state factorisation facilitates the ability to not just discover tools but invent them through the offline induction of an appropriate tool property. We discuss the implications of these preliminary results and outline future directions of research.

Designing Ecosystems of Intelligence from First Principles

This white paper lays out a vision of research and development in the field of artificial intelligence for the next decade (and beyond). Its denouement is a cyber-physical ecosystem of natural and synthetic sense-making, in which humans are integral participants$\unicode{x2014}$what we call ''shared intelligence''. This vision is premised on active inference, a formulation of adaptive behavior that can be read as a physics of intelligence, and which inherits from the physics of self-organization. In this context, we understand intelligence as the capacity to accumulate evidence for a generative model of one's sensed world$\unicode{x2014}$also known as self-evidencing. Formally, this corresponds to maximizing (Bayesian) model evidence, via belief updating over several scales: i.e., inference, learning, and model selection. Operationally, this self-evidencing can be realized via (variational) message passing or belief propagation on a factor graph. Crucially, active inference foregrounds an existential imperative of intelligent systems; namely, curiosity or the resolution of uncertainty. This same imperative underwrites belief sharing in ensembles of agents, in which certain aspects (i.e., factors) of each agent's generative world model provide a common ground or frame of reference. Active inference plays a foundational role in this ecology of belief sharing$\unicode{x2014}$leading to a formal account of collective intelligence that rests on shared narratives and goals. We also consider the kinds of communication protocols that must be developed to enable such an ecosystem of intelligences and motivate the development of a shared hyper-spatial modeling language and transaction protocol, as a first$\unicode{x2014}$and key$\unicode{x2014}$step towards such an ecology.

Preventing Deterioration of Classification Accuracy in Predictive Coding Networks

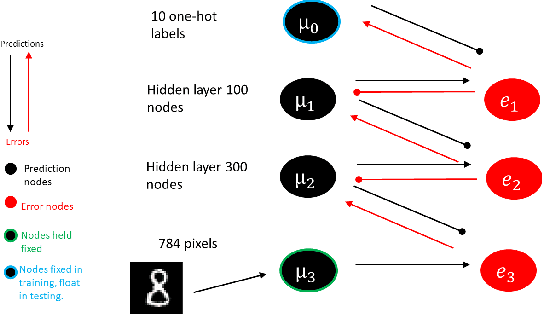
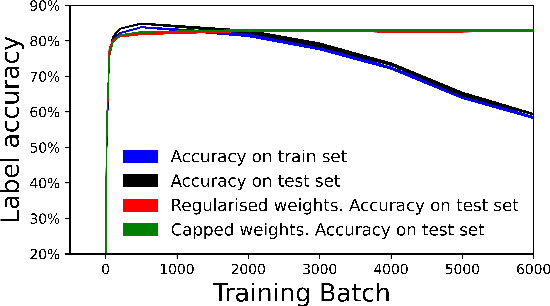
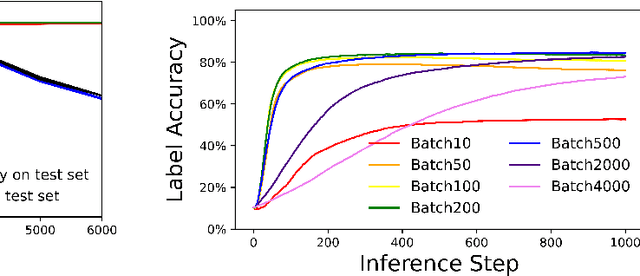
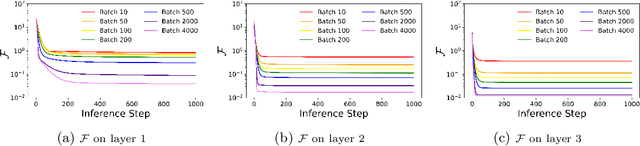
Predictive Coding Networks (PCNs) aim to learn a generative model of the world. Given observations, this generative model can then be inverted to infer the causes of those observations. However, when training PCNs, a noticeable pathology is often observed where inference accuracy peaks and then declines with further training. This cannot be explained by overfitting since both training and test accuracy decrease simultaneously. Here we provide a thorough investigation of this phenomenon and show that it is caused by an imbalance between the speeds at which the various layers of the PCN converge. We demonstrate that this can be prevented by regularising the weight matrices at each layer: by restricting the relative size of matrix singular values, we allow the weight matrix to change but restrict the overall impact which a layer can have on its neighbours. We also demonstrate that a similar effect can be achieved through a more biologically plausible and simple scheme of just capping the weights.

Successor Representation Active Inference

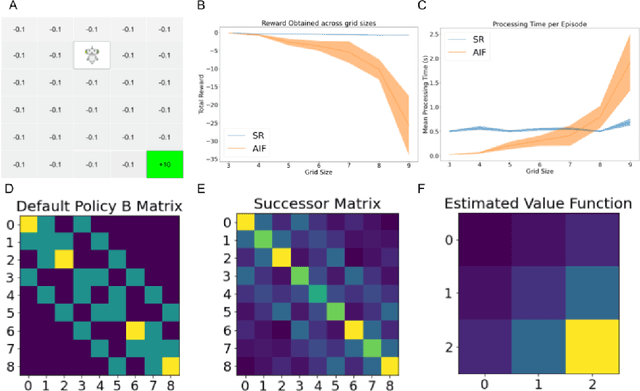
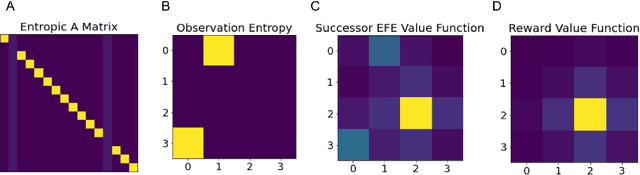
Recent work has uncovered close links between between classical reinforcement learning algorithms, Bayesian filtering, and Active Inference which lets us understand value functions in terms of Bayesian posteriors. An alternative, but less explored, model-free RL algorithm is the successor representation, which expresses the value function in terms of a successor matrix of expected future state occupancies. In this paper, we derive the probabilistic interpretation of the successor representation in terms of Bayesian filtering and thus design a novel active inference agent architecture utilizing successor representations instead of model-based planning. We demonstrate that active inference successor representations have significant advantages over current active inference agents in terms of planning horizon and computational cost. Moreover, we demonstrate how the successor representation agent can generalize to changing reward functions such as variants of the expected free energy.

RL with KL penalties is better viewed as Bayesian inference

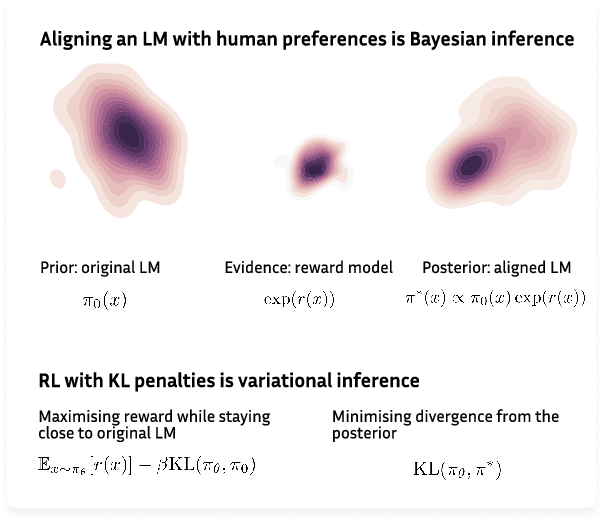
Reinforcement learning (RL) is frequently employed in fine-tuning large language models (LMs), such as GPT-3, to penalize them for undesirable features of generated sequences, such as offensiveness, social bias, harmfulness or falsehood. The RL formulation involves treating the LM as a policy and updating it to maximise the expected value of a reward function which captures human preferences, such as non-offensiveness. In this paper, we analyze challenges associated with treating a language model as an RL policy and show how avoiding those challenges requires moving beyond the RL paradigm. We start by observing that the standard RL approach is flawed as an objective for fine-tuning LMs because it leads to distribution collapse: turning the LM into a degenerate distribution. Then, we analyze KL-regularised RL, a widely used recipe for fine-tuning LMs, which additionally constrains the fine-tuned LM to stay close to its original distribution in terms of Kullback-Leibler (KL) divergence. We show that KL-regularised RL is equivalent to variational inference: approximating a Bayesian posterior which specifies how to update a prior LM to conform with evidence provided by the reward function. We argue that this Bayesian inference view of KL-regularised RL is more insightful than the typically employed RL perspective. The Bayesian inference view explains how KL-regularised RL avoids the distribution collapse problem and offers a first-principles derivation for its objective. While this objective happens to be equivalent to RL (with a particular choice of parametric reward), there exist other objectives for fine-tuning LMs which are no longer equivalent to RL. That observation leads to a more general point: RL is not an adequate formal framework for problems such as fine-tuning language models. These problems are best viewed as Bayesian inference: approximating a pre-defined target distribution.

Hybrid Predictive Coding: Inferring, Fast and Slow

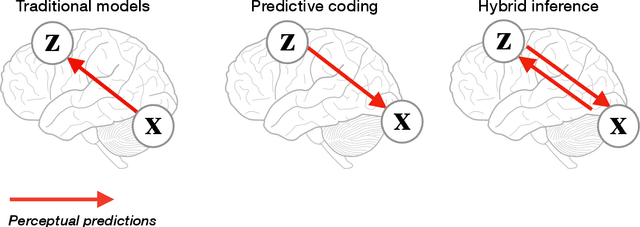
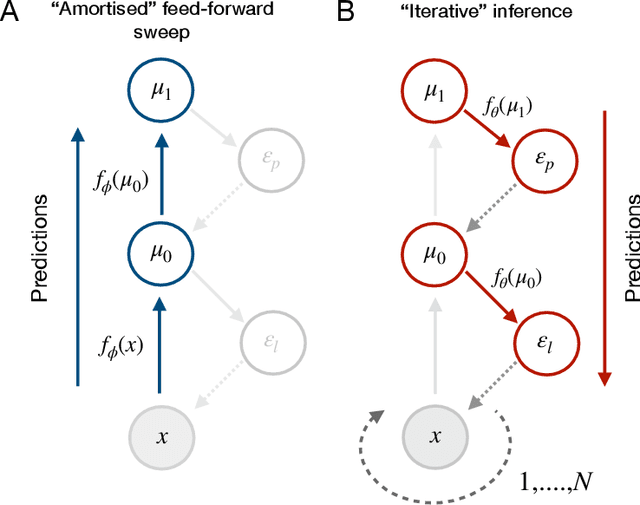
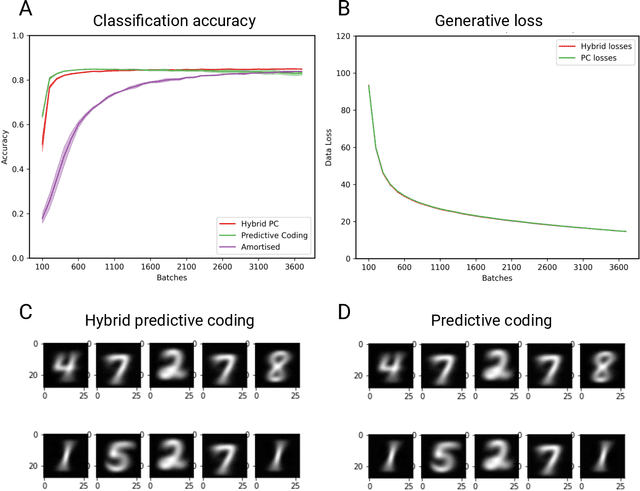
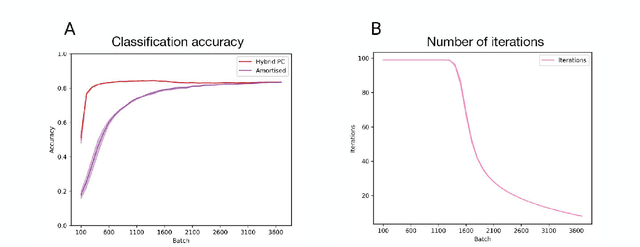
Predictive coding is an influential model of cortical neural activity. It proposes that perceptual beliefs are furnished by sequentially minimising "prediction errors" - the differences between predicted and observed data. Implicit in this proposal is the idea that perception requires multiple cycles of neural activity. This is at odds with evidence that several aspects of visual perception - including complex forms of object recognition - arise from an initial "feedforward sweep" that occurs on fast timescales which preclude substantial recurrent activity. Here, we propose that the feedforward sweep can be understood as performing amortized inference and recurrent processing can be understood as performing iterative inference. We propose a hybrid predictive coding network that combines both iterative and amortized inference in a principled manner by describing both in terms of a dual optimization of a single objective function. We show that the resulting scheme can be implemented in a biologically plausible neural architecture that approximates Bayesian inference utilising local Hebbian update rules. We demonstrate that our hybrid predictive coding model combines the benefits of both amortized and iterative inference -- obtaining rapid and computationally cheap perceptual inference for familiar data while maintaining the context-sensitivity, precision, and sample efficiency of iterative inference schemes. Moreover, we show how our model is inherently sensitive to its uncertainty and adaptively balances iterative and amortized inference to obtain accurate beliefs using minimum computational expense. Hybrid predictive coding offers a new perspective on the functional relevance of the feedforward and recurrent activity observed during visual perception and offers novel insights into distinct aspects of visual phenomenology.

A Mathematical Walkthrough and Discussion of the Free Energy Principle

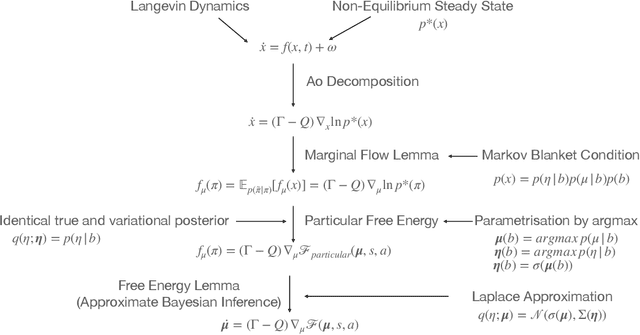
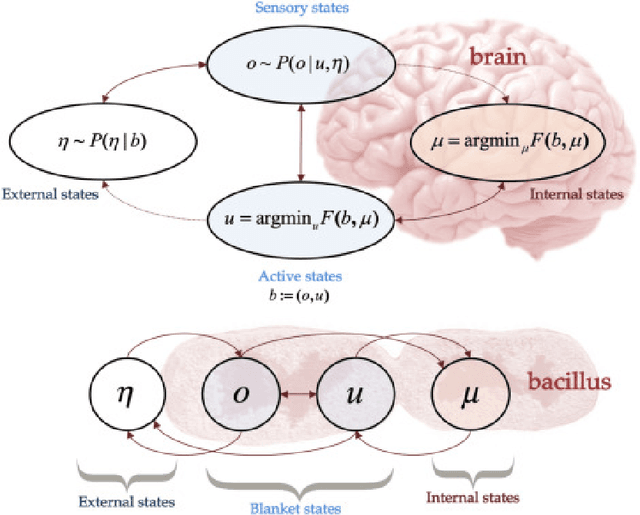
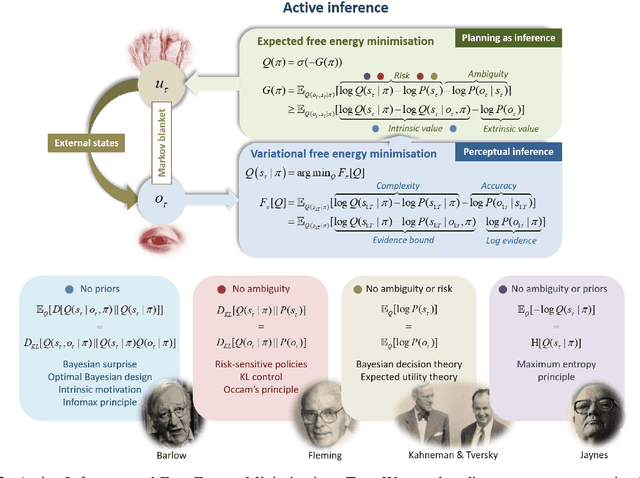
The Free-Energy-Principle (FEP) is an influential and controversial theory which postulates a deep and powerful connection between the stochastic thermodynamics of self-organization and learning through variational inference. Specifically, it claims that any self-organizing system which can be statistically separated from its environment, and which maintains itself at a non-equilibrium steady state, can be construed as minimizing an information-theoretic functional -- the variational free energy -- and thus performing variational Bayesian inference to infer the hidden state of its environment. This principle has also been applied extensively in neuroscience, and is beginning to make inroads in machine learning by spurring the construction of novel and powerful algorithms by which action, perception, and learning can all be unified under a single objective. While its expansive and often grandiose claims have spurred significant debates in both philosophy and theoretical neuroscience, the mathematical depth and lack of accessible introductions and tutorials for the core claims of the theory have often precluded a deep understanding within the literature. Here, we aim to provide a mathematically detailed, yet intuitive walk-through of the formulation and central claims of the FEP while also providing a discussion of the assumptions necessary and potential limitations of the theory. Additionally, since the FEP is a still a living theory, subject to internal controversy, change, and revision, we also present a detailed appendix highlighting and condensing current perspectives as well as controversies about the nature, applicability, and the mathematical assumptions and formalisms underlying the FEP.