Gradient-free variational learning with conditional mixture networks

Balancing computational efficiency with robust predictive performance is crucial in supervised learning, especially for critical applications. Standard deep learning models, while accurate and scalable, often lack probabilistic features like calibrated predictions and uncertainty quantification. Bayesian methods address these issues but can be computationally expensive as model and data complexity increase. Previous work shows that fast variational methods can reduce the compute requirements of Bayesian methods by eliminating the need for gradient computation or sampling, but are often limited to simple models. We demonstrate that conditional mixture networks (CMNs), a probabilistic variant of the mixture-of-experts (MoE) model, are suitable for fast, gradient-free inference and can solve complex classification tasks. CMNs employ linear experts and a softmax gating network. By exploiting conditional conjugacy and P\'olya-Gamma augmentation, we furnish Gaussian likelihoods for the weights of both the linear experts and the gating network. This enables efficient variational updates using coordinate ascent variational inference (CAVI), avoiding traditional gradient-based optimization. We validate this approach by training two-layer CMNs on standard benchmarks from the UCI repository. Our method, CAVI-CMN, achieves competitive and often superior predictive accuracy compared to maximum likelihood estimation (MLE) with backpropagation, while maintaining competitive runtime and full posterior distributions over all model parameters. Moreover, as input size or the number of experts increases, computation time scales competitively with MLE and other gradient-based solutions like black-box variational inference (BBVI), making CAVI-CMN a promising tool for deep, fast, and gradient-free Bayesian networks.

From pixels to planning: scale-free active inference

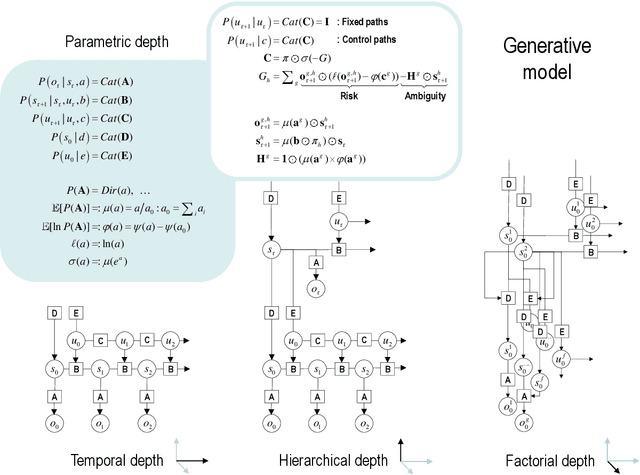
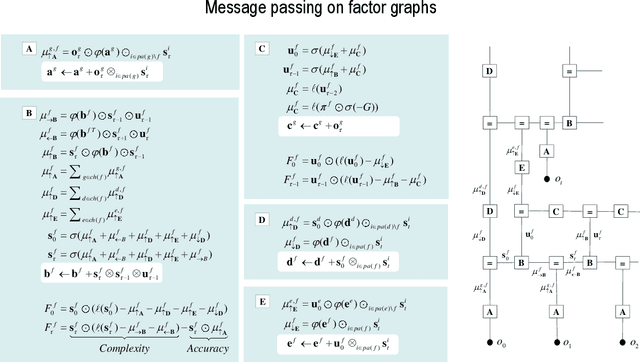
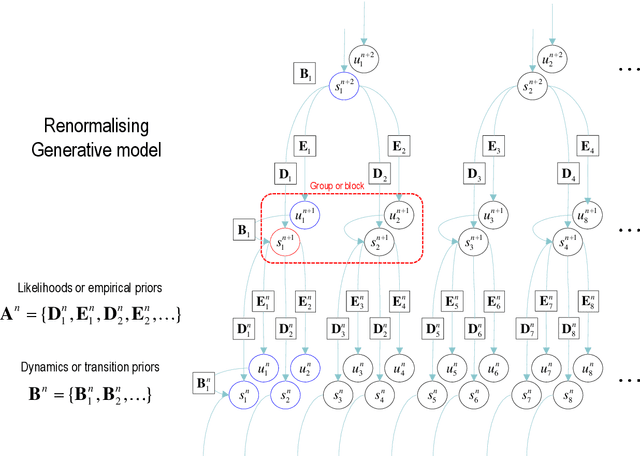
This paper describes a discrete state-space model -- and accompanying methods -- for generative modelling. This model generalises partially observed Markov decision processes to include paths as latent variables, rendering it suitable for active inference and learning in a dynamic setting. Specifically, we consider deep or hierarchical forms using the renormalisation group. The ensuing renormalising generative models (RGM) can be regarded as discrete homologues of deep convolutional neural networks or continuous state-space models in generalised coordinates of motion. By construction, these scale-invariant models can be used to learn compositionality over space and time, furnishing models of paths or orbits; i.e., events of increasing temporal depth and itinerancy. This technical note illustrates the automatic discovery, learning and deployment of RGMs using a series of applications. We start with image classification and then consider the compression and generation of movies and music. Finally, we apply the same variational principles to the learning of Atari-like games.

Supervised structure learning

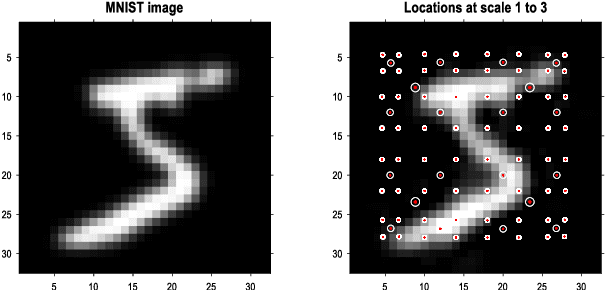
This paper concerns structure learning or discovery of discrete generative models. It focuses on Bayesian model selection and the assimilation of training data or content, with a special emphasis on the order in which data are ingested. A key move - in the ensuing schemes - is to place priors on the selection of models, based upon expected free energy. In this setting, expected free energy reduces to a constrained mutual information, where the constraints inherit from priors over outcomes (i.e., preferred outcomes). The resulting scheme is first used to perform image classification on the MNIST dataset to illustrate the basic idea, and then tested on a more challenging problem of discovering models with dynamics, using a simple sprite-based visual disentanglement paradigm and the Tower of Hanoi (cf., blocks world) problem. In these examples, generative models are constructed autodidactically to recover (i.e., disentangle) the factorial structure of latent states - and their characteristic paths or dynamics.

An empirical evaluation of active inference in multi-armed bandits

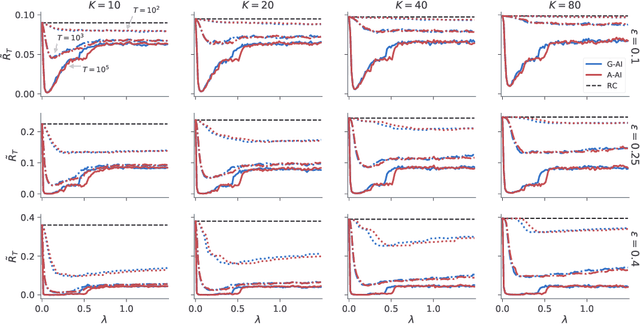
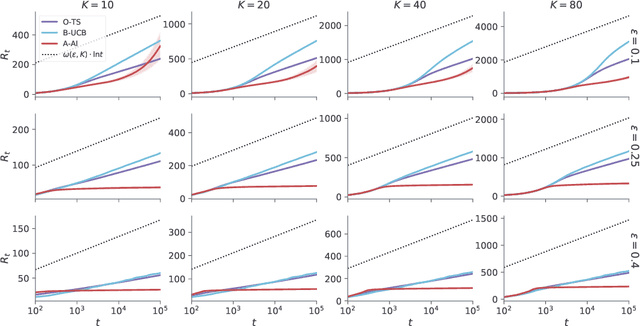
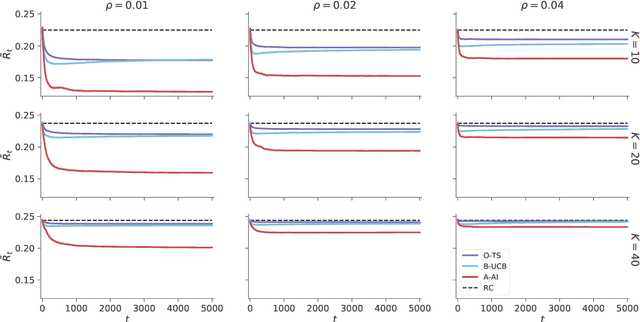
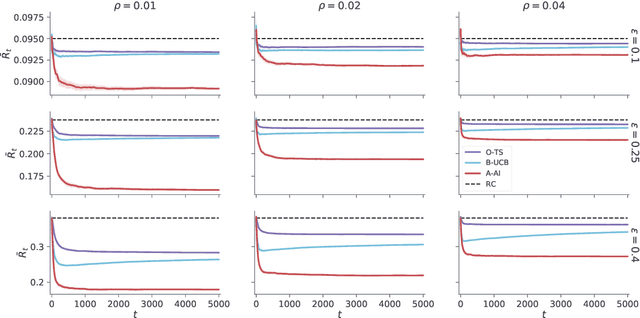
A key feature of sequential decision making under uncertainty is a need to balance between exploiting--choosing the best action according to the current knowledge, and exploring--obtaining information about values of other actions. The multi-armed bandit problem, a classical task that captures this trade-off, served as a vehicle in machine learning for developing bandit algorithms that proved to be useful in numerous industrial applications. The active inference framework, an approach to sequential decision making recently developed in neuroscience for understanding human and animal behaviour, is distinguished by its sophisticated strategy for resolving the exploration-exploitation trade-off. This makes active inference an exciting alternative to already established bandit algorithms. Here we derive an efficient and scalable approximate active inference algorithm and compare it to two state-of-the-art bandit algorithms: Bayesian upper confidence bound and optimistic Thompson sampling. This comparison is done on two types of bandit problems: a stationary and a dynamic switching bandit. Our empirical evaluation shows that the active inference algorithm does not produce efficient long-term behaviour in stationary bandits. However, in the more challenging switching bandit problem active inference performs substantially better than the two state-of-the-art bandit algorithms. The results open exciting venues for further research in theoretical and applied machine learning, as well as lend additional credibility to active inference as a general framework for studying human and animal behaviour.