Marcus Valtonen Örnhag
Radially Distorted Homographies, Revisited
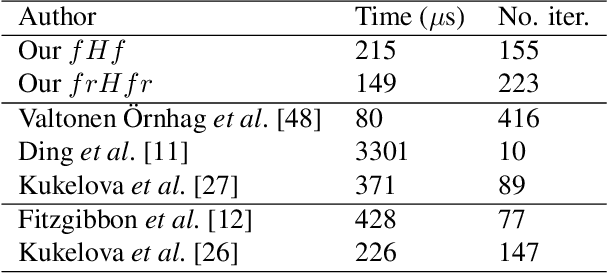
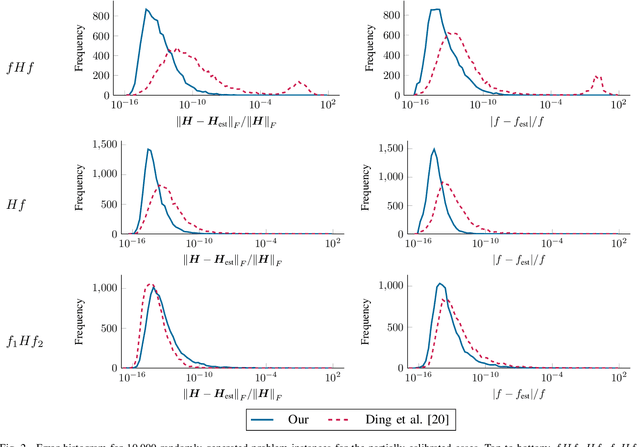
Aug 28, 2025Abstract:Homographies are among the most prevalent transformations occurring in geometric computer vision and projective geometry, and homography estimation is consequently a crucial step in a wide assortment of computer vision tasks. When working with real images, which are often afflicted with geometric distortions caused by the camera lens, it may be necessary to determine both the homography and the lens distortion-particularly the radial component, called radial distortion-simultaneously to obtain anything resembling useful estimates. When considering a homography with radial distortion between two images, there are three conceptually distinct configurations for the radial distortion; (i) distortion in only one image, (ii) identical distortion in the two images, and (iii) independent distortion in the two images. While these cases have been addressed separately in the past, the present paper provides a novel and unified approach to solve all three cases. We demonstrate how the proposed approach can be used to construct new fast, stable, and accurate minimal solvers for radially distorted homographies. In all three cases, our proposed solvers are faster than the existing state-of-the-art solvers while maintaining similar accuracy. The solvers are tested on well-established benchmarks including images taken with fisheye cameras. The source code for our solvers will be made available in the event our paper is accepted for publication.
Trust Your IMU: Consequences of Ignoring the IMU Drift
Mar 16, 2021



Abstract:In this paper, we argue that modern pre-integration methods for inertial measurement units (IMUs) are accurate enough to ignore the drift for short time intervals. This allows us to consider a simplified camera model, which in turn admits further intrinsic calibration. We develop the first-ever solver to jointly solve the relative pose problem with unknown and equal focal length and radial distortion profile while utilizing the IMU data. Furthermore, we show significant speed-up compared to state-of-the-art algorithms, with small or negligible loss in accuracy for partially calibrated setups. The proposed algorithms are tested on both synthetic and real data, where the latter is focused on navigation using unmanned aerial vehicles (UAVs). We evaluate the proposed solvers on different commercially available low-cost UAVs, and demonstrate that the novel assumption on IMU drift is feasible in real-life applications. The extended intrinsic auto-calibration enables us to use distorted input images, making tedious calibration processes obsolete, compared to current state-of-the-art methods.
Efficient Real-Time Radial Distortion Correction for UAVs
Oct 08, 2020
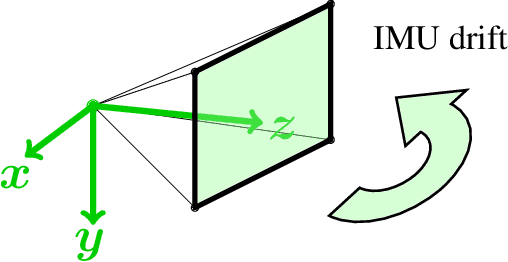

Abstract:In this paper we present a novel algorithm for onboard radial distortion correction for unmanned aerial vehicles (UAVs) equipped with an inertial measurement unit (IMU), that runs in real-time. This approach makes calibration procedures redundant, thus allowing for exchange of optics extemporaneously. By utilizing the IMU data, the cameras can be aligned with the gravity direction. This allows us to work with fewer degrees of freedom, and opens up for further intrinsic calibration. We propose a fast and robust minimal solver for simultaneously estimating the focal length, radial distortion profile and motion parameters from homographies. The proposed solver is tested on both synthetic and real data, and perform better or on par with state-of-the-art methods relying on pre-calibration procedures.
Accurate Optimization of Weighted Nuclear Norm for Non-Rigid Structure from Motion
Mar 23, 2020
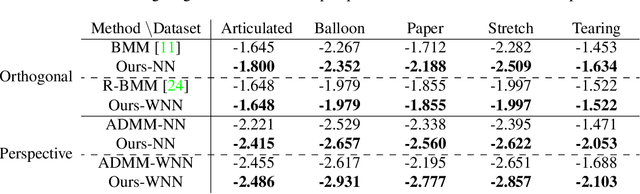

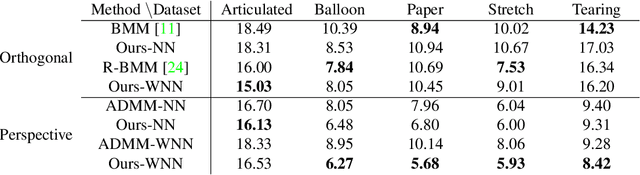
Abstract:Fitting a matrix of a given rank to data in a least squares sense can be done very effectively using 2nd order methods such as Levenberg-Marquardt by explicitly optimizing over a bilinear parameterization of the matrix. In contrast, when applying more general singular value penalties, such as weighted nuclear norm priors, direct optimization over the elements of the matrix is typically used. Due to non-differentiability of the resulting objective function, first order sub-gradient or splitting methods are predominantly used. While these offer rapid iterations it is well known that they become inefficent near the minimum due to zig-zagging and in practice one is therefore often forced to settle for an approximate solution. In this paper we show that more accurate results can in many cases be achieved with 2nd order methods. Our main result shows how to construct bilinear formulations, for a general class of regularizers including weighted nuclear norm penalties, that are provably equivalent to the original problems. With these formulations the regularizing function becomes twice differentiable and 2nd order methods can be applied. We show experimentally, on a number of structure from motion problems, that our approach outperforms state-of-the-art methods.
Minimal Solvers for Indoor UAV Positioning
Mar 16, 2020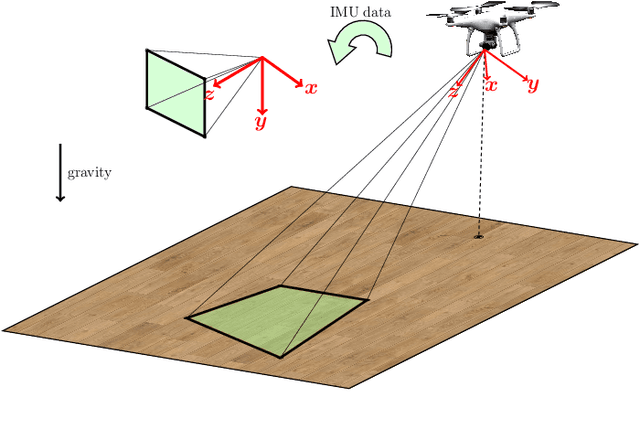


Abstract:In this paper we consider a collection of relative pose problems which arise naturally in applications for visual indoor UAV navigation. We focus on cases where additional information from an onboard IMU is available and thus provides a partial extrinsic calibration through the gravitational vector. The solvers are designed for a partially calibrated camera, for a variety of realistic indoor scenarios, which makes it possible to navigate using images of the ground floor. Current state-of-the-art solvers use more general assumptions, such as using arbitrary planar structures; however, these solvers do not yield adequate reconstructions for real scenes, nor do they perform fast enough to be incorporated in real-time systems. We show that the proposed solvers enjoy better numerical stability, are faster, and require fewer point correspondences, compared to state-of-the-art solvers. These properties are vital components for robust navigation in real-time systems, and we demonstrate on both synthetic and real data that our method outperforms other methods, and yields superior motion estimation.
Bilinear Parameterization For Differentiable Rank-Regularization
Dec 07, 2018

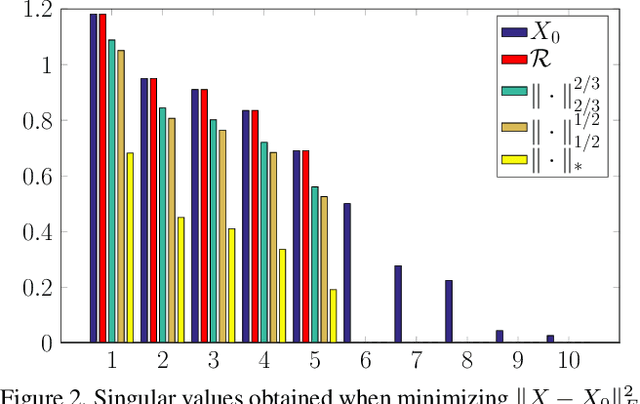
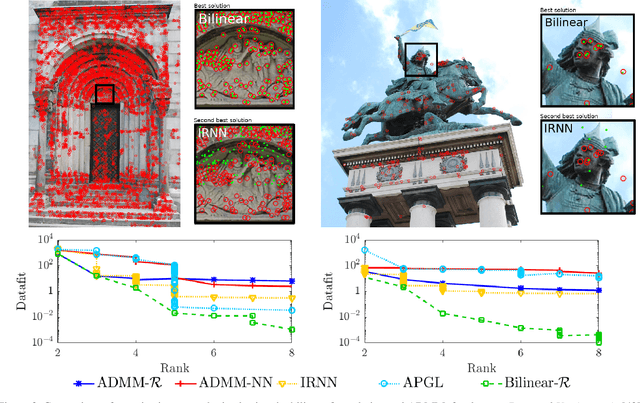
Abstract:Low rank approximation is a commonly occurring problem in many computer vision and machine learning applications. There are two common ways of optimizing the resulting models. Either the set of matrices with a given sought rank can be explicitly parametrized using a bilinear factorization, or low rank can be implicitly enforced using regularization terms penalizing non-zero singular values. While the former results in differentiable problems that can be efficiently optimized using local quadratic approximation the latter are typically not differentiable (sometimes even discontinuous) and require splitting methods such as Alternating Direction Method of Multipliers (ADMM). It is well known that while ADMM makes rapid improvements the first couple of iterations convergence to the exact minimizer can be tediously slow. On the other hand regularization formulations can in certain cases come with theoretical optimality guarantees. In this paper we show how many non-differentiable regularization methods can be reformulated into smooth objectives using bilinear parameterization. This opens up the possibility of using second order methods such as Levenberg--Marquardt (LM) and Variable Projection (VarPro) to achieve accurate solutions for ill-conditioned problems. We show on several real and synthetic experiments that our second order formulation converges to substantially more accurate solutions than what ADMM formulations provide in a reasonable amount of time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge