QuaMo: Quaternion Motions for Vision-based 3D Human Kinematics Capture

Vision-based 3D human motion capture from videos remains a challenge in computer vision. Traditional 3D pose estimation approaches often ignore the temporal consistency between frames, causing implausible and jittery motion. The emerging field of kinematics-based 3D motion capture addresses these issues by estimating the temporal transitioning between poses instead. A major drawback in current kinematics approaches is their reliance on Euler angles. Despite their simplicity, Euler angles suffer from discontinuity that leads to unstable motion reconstructions, especially in online settings where trajectory refinement is unavailable. Contrarily, quaternions have no discontinuity and can produce continuous transitions between poses. In this paper, we propose QuaMo, a novel Quaternion Motions method using quaternion differential equations (QDE) for human kinematics capture. We utilize the state-space model, an effective system for describing real-time kinematics estimations, with quaternion state and the QDE describing quaternion velocity. The corresponding angular acceleration is computed from a meta-PD controller with a novel acceleration enhancement that adaptively regulates the control signals as the human quickly changes to a new pose. Unlike previous work, our QDE is solved under the quaternion unit-sphere constraint that results in more accurate estimations. Experimental results show that our novel formulation of the QDE with acceleration enhancement accurately estimates 3D human kinematics with no discontinuity and minimal implausibilities. QuaMo outperforms comparable state-of-the-art methods on multiple datasets, namely Human3.6M, Fit3D, SportsPose and AIST. The code is available at https://github.com/cuongle1206/QuaMo

Flow Matching for Probabilistic Monocular 3D Human Pose Estimation

Recovering 3D human poses from a monocular camera view is a highly ill-posed problem due to the depth ambiguity. Earlier studies on 3D human pose lifting from 2D often contain incorrect-yet-overconfident 3D estimations. To mitigate the problem, emerging probabilistic approaches treat the 3D estimations as a distribution, taking into account the uncertainty measurement of the poses. Falling in a similar category, we proposed FMPose, a probabilistic 3D human pose estimation method based on the flow matching generative approach. Conditioned on the 2D cues, the flow matching scheme learns the optimal transport from a simple source distribution to the plausible 3D human pose distribution via continuous normalizing flows. The 2D lifting condition is modeled via graph convolutional networks, leveraging the learnable connections between human body joints as the graph structure for feature aggregation. Compared to diffusion-based methods, the FMPose with optimal transport produces faster and more accurate 3D pose generations. Experimental results show major improvements of our FMPose over current state-of-the-art methods on three common benchmarks for 3D human pose estimation, namely Human3.6M, MPI-INF-3DHP and 3DPW.

RoMa v2: Harder Better Faster Denser Feature Matching

Dense feature matching aims to estimate all correspondences between two images of a 3D scene and has recently been established as the gold-standard due to its high accuracy and robustness. However, existing dense matchers still fail or perform poorly for many hard real-world scenarios, and high-precision models are often slow, limiting their applicability. In this paper, we attack these weaknesses on a wide front through a series of systematic improvements that together yield a significantly better model. In particular, we construct a novel matching architecture and loss, which, combined with a curated diverse training distribution, enables our model to solve many complex matching tasks. We further make training faster through a decoupled two-stage matching-then-refinement pipeline, and at the same time, significantly reduce refinement memory usage through a custom CUDA kernel. Finally, we leverage the recent DINOv3 foundation model along with multiple other insights to make the model more robust and unbiased. In our extensive set of experiments we show that the resulting novel matcher sets a new state-of-the-art, being significantly more accurate than its predecessors. Code is available at https://github.com/Parskatt/romav2

Radially Distorted Homographies, Revisited

Homographies are among the most prevalent transformations occurring in geometric computer vision and projective geometry, and homography estimation is consequently a crucial step in a wide assortment of computer vision tasks. When working with real images, which are often afflicted with geometric distortions caused by the camera lens, it may be necessary to determine both the homography and the lens distortion-particularly the radial component, called radial distortion-simultaneously to obtain anything resembling useful estimates. When considering a homography with radial distortion between two images, there are three conceptually distinct configurations for the radial distortion; (i) distortion in only one image, (ii) identical distortion in the two images, and (iii) independent distortion in the two images. While these cases have been addressed separately in the past, the present paper provides a novel and unified approach to solve all three cases. We demonstrate how the proposed approach can be used to construct new fast, stable, and accurate minimal solvers for radially distorted homographies. In all three cases, our proposed solvers are faster than the existing state-of-the-art solvers while maintaining similar accuracy. The solvers are tested on well-established benchmarks including images taken with fisheye cameras. The source code for our solvers will be made available in the event our paper is accepted for publication.

DaD: Distilled Reinforcement Learning for Diverse Keypoint Detection

Keypoints are what enable Structure-from-Motion (SfM) systems to scale to thousands of images. However, designing a keypoint detection objective is a non-trivial task, as SfM is non-differentiable. Typically, an auxiliary objective involving a descriptor is optimized. This however induces a dependency on the descriptor, which is undesirable. In this paper we propose a fully self-supervised and descriptor-free objective for keypoint detection, through reinforcement learning. To ensure training does not degenerate, we leverage a balanced top-K sampling strategy. While this already produces competitive models, we find that two qualitatively different types of detectors emerge, which are only able to detect light and dark keypoints respectively. To remedy this, we train a third detector, DaD, that optimizes the Kullback-Leibler divergence of the pointwise maximum of both light and dark detectors. Our approach significantly improve upon SotA across a range of benchmarks. Code and model weights are publicly available at https://github.com/parskatt/dad

DeDoDe: Detect, Don't Describe -- Describe, Don't Detect for Local Feature Matching

Keypoint detection is a pivotal step in 3D reconstruction, whereby sets of (up to) K points are detected in each view of a scene. Crucially, the detected points need to be consistent between views, i.e., correspond to the same 3D point in the scene. One of the main challenges with keypoint detection is the formulation of the learning objective. Previous learning-based methods typically jointly learn descriptors with keypoints, and treat the keypoint detection as a binary classification task on mutual nearest neighbours. However, basing keypoint detection on descriptor nearest neighbours is a proxy task, which is not guaranteed to produce 3D-consistent keypoints. Furthermore, this ties the keypoints to a specific descriptor, complicating downstream usage. In this work, we instead learn keypoints directly from 3D consistency. To this end, we train the detector to detect tracks from large-scale SfM. As these points are often overly sparse, we derive a semi-supervised two-view detection objective to expand this set to a desired number of detections. To train a descriptor, we maximize the mutual nearest neighbour objective over the keypoints with a separate network. Results show that our approach, DeDoDe, achieves significant gains on multiple geometry benchmarks. Code is provided at https://github.com/Parskatt/DeDoDe

Deep Equivariant Hyperspheres

This paper presents an approach to learning nD features equivariant under orthogonal transformations for point cloud analysis, utilizing hyperspheres and regular n-simplexes. Our main contributions are theoretical and tackle major issues in geometric deep learning such as equivariance and invariance under geometric transformations. Namely, we enrich the recently developed theory of steerable 3D spherical neurons -- SO(3)-equivariant filter banks based on neurons with spherical decision surfaces -- by extending said neurons to nD, which we call deep equivariant hyperspheres, and enabling their stacking in multiple layers. Using the ModelNet40 benchmark, we experimentally verify our theoretical contributions and show a potential practical configuration of the proposed equivariant hyperspheres.

RoMa: Revisiting Robust Losses for Dense Feature Matching

Dense feature matching is an important computer vision task that involves estimating all correspondences between two images of a 3D scene. In this paper, we revisit robust losses for matching from a Markov chain perspective, yielding theoretical insights and large gains in performance. We begin by constructing a unifying formulation of matching as a Markov chain, based on which we identify two key stages which we argue should be decoupled for matching. The first is the coarse stage, where the estimated result needs to be globally consistent. The second is the refinement stage, where the model needs precise localization capabilities. Inspired by the insight that these stages concern distinct issues, we propose a coarse matcher following the regression-by-classification paradigm that provides excellent globally consistent, albeit not exactly localized, matches. This is followed by a local feature refinement stage using well-motivated robust regression losses, yielding extremely precise matches. Our proposed approach, which we call RoMa, achieves significant improvements compared to the state-of-the-art. Code is available at https://github.com/Parskatt/RoMa

TetraSphere: A Neural Descriptor for O(3)-Invariant Point Cloud Classification

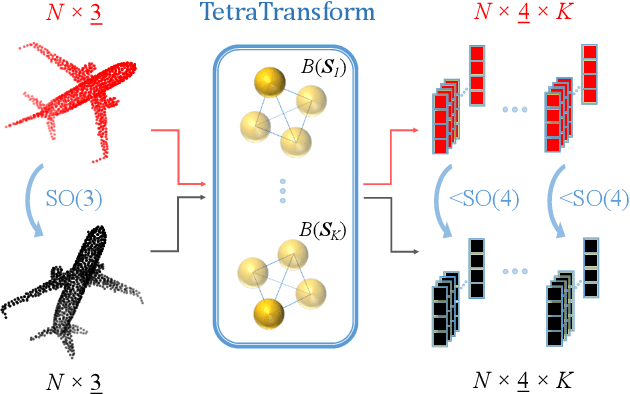
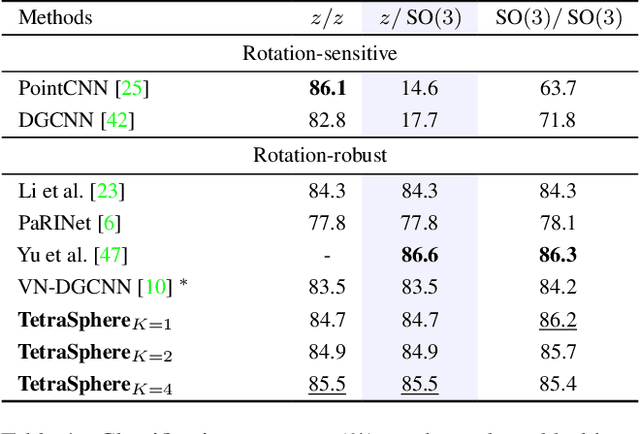
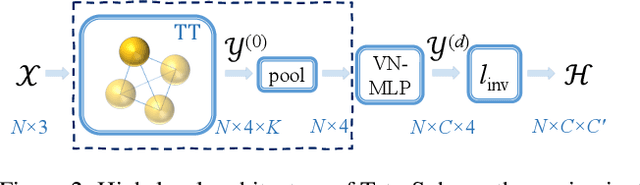
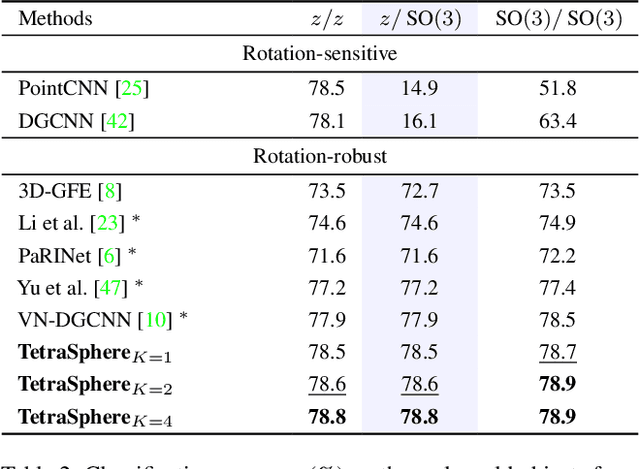
Rotation invariance is an important requirement for the analysis of 3D point clouds. In this paper, we present TetraSphere -- a learnable descriptor for rotation- and reflection-invariant 3D point cloud classification based on recently introduced steerable 3D spherical neurons and vector neurons, as well as the Gram matrix method. Taking 3D points as input, TetraSphere performs TetraTransform -- lifts the 3D input to 4D -- and extracts rotation-equivariant features, subsequently computing pair-wise O(3)-invariant inner products of these features. Remarkably, TetraSphere can be embedded into common point cloud processing models. We demonstrate its effectiveness and versatility by integrating it into DGCNN and VN-DGCNN, performing the classification of arbitrarily rotated ModelNet40 shapes. We show that using TetraSphere improves the performance and reduces the computational complexity by about 10% of the respective baseline methods.

Deep Kernelized Dense Geometric Matching

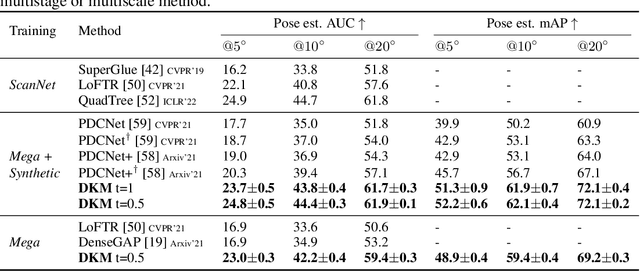
Dense geometric matching is a challenging computer vision task, requiring accurate correspondences under extreme variations in viewpoint and illumination, even for low-texture regions. In this task, finding accurate global correspondences is essential for later refinement stages. The current learning based paradigm is to perform global fixed-size correlation, followed by flattening and convolution to predict correspondences. In this work, we consider the problem from a different perspective and propose to formulate global correspondence estimation as a continuous probabilistic regression task using deep kernels, yielding a novel approach to learning dense correspondences. Our full approach, \textbf{D}eep \textbf{K}ernelized \textbf{M}atching, achieves significant improvements compared to the state-of-the-art on the competitive HPatches and YFCC100m benchmarks, and we dissect the gains of our contributions in a thorough ablation study.