ICML 2023 Topological Deep Learning Challenge : Design and Results

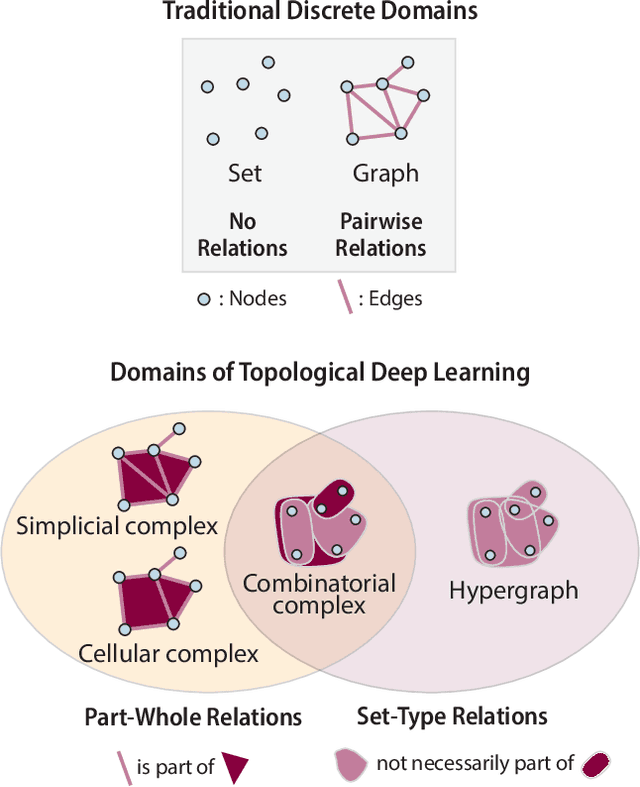
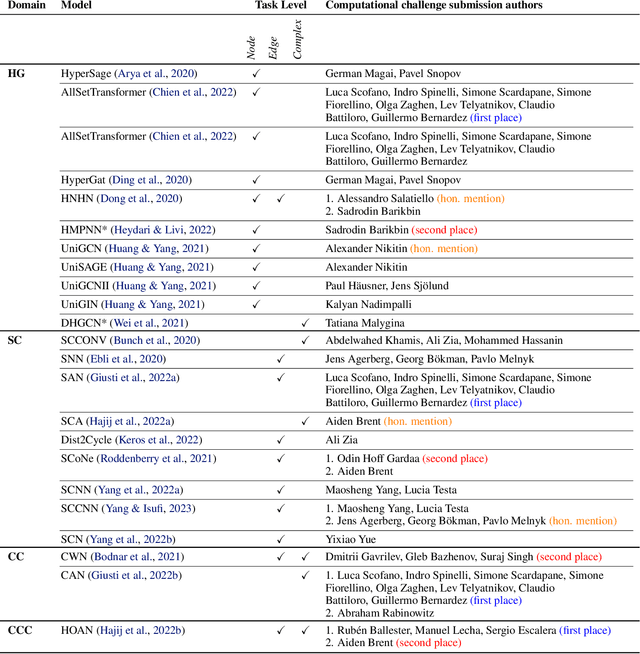
This paper presents the computational challenge on topological deep learning that was hosted within the ICML 2023 Workshop on Topology and Geometry in Machine Learning. The competition asked participants to provide open-source implementations of topological neural networks from the literature by contributing to the python packages TopoNetX (data processing) and TopoModelX (deep learning). The challenge attracted twenty-eight qualifying submissions in its two-month duration. This paper describes the design of the challenge and summarizes its main findings.

Augment Features Beyond Color for Domain Generalized Segmentation

Domain generalized semantic segmentation (DGSS) is an essential but highly challenging task, in which the model is trained only on source data and any target data is not available. Previous DGSS methods can be partitioned into augmentation-based and normalization-based ones. The former either introduces extra biased data or only conducts channel-wise adjustments for data augmentation, and the latter may discard beneficial visual information, both of which lead to limited performance in DGSS. Contrarily, our method performs inter-channel transformation and meanwhile evades domain-specific biases, thus diversifying data and enhancing model generalization performance. Specifically, our method consists of two modules: random image color augmentation (RICA) and random feature distribution augmentation (RFDA). RICA converts images from RGB to the CIELAB color model and randomizes color maps in a perception-based way for image enhancement purposes. We further this augmentation by extending it beyond color to feature space using a CycleGAN-based generative network, which complements RICA and further boosts generalization capability. We conduct extensive experiments, and the generalization results from the synthetic GTAV and SYNTHIA to the real Cityscapes, BDDS, and Mapillary datasets show that our method achieves state-of-the-art performance in DGSS.

Deep Equivariant Hyperspheres

This paper presents an approach to learning nD features equivariant under orthogonal transformations for point cloud analysis, utilizing hyperspheres and regular n-simplexes. Our main contributions are theoretical and tackle major issues in geometric deep learning such as equivariance and invariance under geometric transformations. Namely, we enrich the recently developed theory of steerable 3D spherical neurons -- SO(3)-equivariant filter banks based on neurons with spherical decision surfaces -- by extending said neurons to nD, which we call deep equivariant hyperspheres, and enabling their stacking in multiple layers. Using the ModelNet40 benchmark, we experimentally verify our theoretical contributions and show a potential practical configuration of the proposed equivariant hyperspheres.

TetraSphere: A Neural Descriptor for O(3)-Invariant Point Cloud Classification

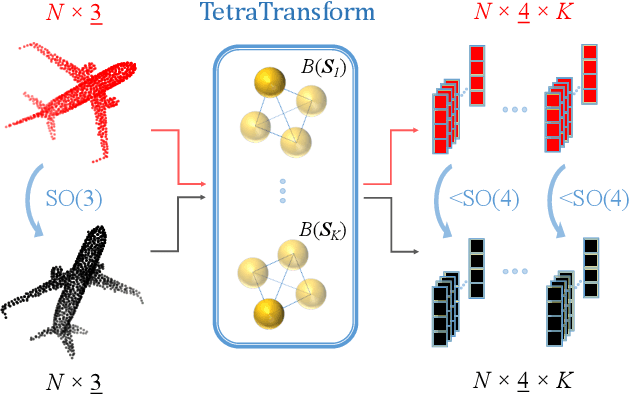
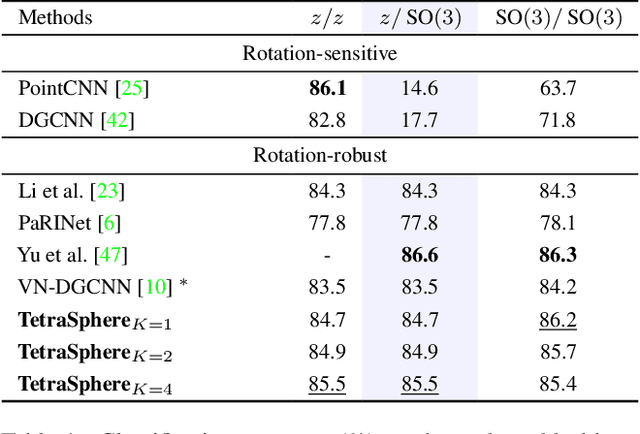
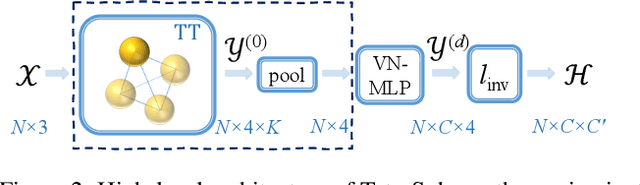
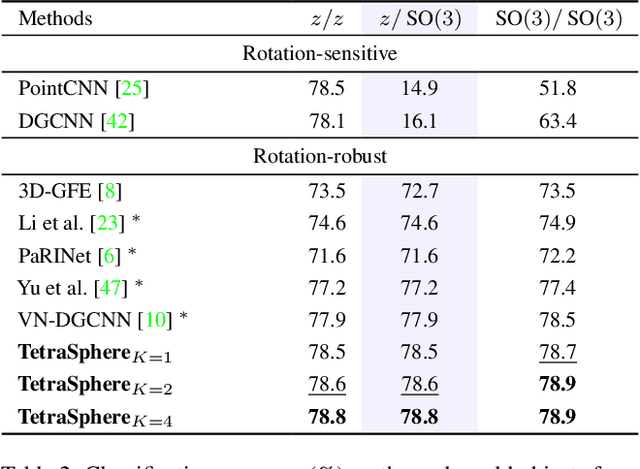
Rotation invariance is an important requirement for the analysis of 3D point clouds. In this paper, we present TetraSphere -- a learnable descriptor for rotation- and reflection-invariant 3D point cloud classification based on recently introduced steerable 3D spherical neurons and vector neurons, as well as the Gram matrix method. Taking 3D points as input, TetraSphere performs TetraTransform -- lifts the 3D input to 4D -- and extracts rotation-equivariant features, subsequently computing pair-wise O(3)-invariant inner products of these features. Remarkably, TetraSphere can be embedded into common point cloud processing models. We demonstrate its effectiveness and versatility by integrating it into DGCNN and VN-DGCNN, performing the classification of arbitrarily rotated ModelNet40 shapes. We show that using TetraSphere improves the performance and reduces the computational complexity by about 10% of the respective baseline methods.

Embed Me If You Can: A Geometric Perceptron

Solving geometric tasks using machine learning is a challenging problem. Standard feed-forward neural networks combine linear or, if the bias parameter is included, affine layers and activation functions. Their geometric modeling is limited, which is why we introduce the alternative model of the multilayer geometric perceptron (MLGP) with units that are geometric neurons, i.e., combinations of hypersphere neurons. The hypersphere neuron is obtained by applying a conformal embedding of Euclidean space. By virtue of Clifford algebra, it can be implemented as the Cartesian dot product. We validate our method on the public 3D Tetris dataset consisting of coordinates of geometric shapes and we show that our method has the capability of generalization over geometric transformations. We demonstrate that our model is superior to the vanilla multilayer perceptron (MLP) while having fewer parameters and no activation function in the hidden layers other than the embedding. In the presence of noise in the data, our model is also superior to the multilayer hypersphere perceptron (MLHP) proposed in prior work. In contrast to the latter, our method reflects the 3D-geometry and provides a topological interpretation of the learned coefficients in the geometric neurons.

A High-Performance CNN Method for Offline Handwritten Chinese Character Recognition and Visualization

Recent researches introduced fast, compact and efficient convolutional neural networks (CNNs) for offline handwritten Chinese character recognition (HCCR). However, many of them did not address the problem of the network interpretability. We propose a new architecture of a deep CNN with a high recognition performance which is capable of learning deep features for visualization. A special characteristic of our model is the bottleneck layers which enable us to retain its expressiveness while reducing the number of multiply-accumulate operations and the required storage. We introduce a modification of global weighted average pooling (GWAP) - global weighted output average pooling (GWOAP). This paper demonstrates how they allow us to calculate class activation maps (CAMs) in order to indicate the most relevant input character image regions used by our CNN to identify a certain class. Evaluating on the ICDAR-2013 offline HCCR competition dataset, we show that our model enables a relative 0.83% error reduction having 49% fewer parameters and the same computational cost compared to the current state-of-the-art single-network method trained only on handwritten data. Our solution outperforms even recent residual learning approaches.