MINN: Learning the dynamics of differential-algebraic equations and application to battery modeling

The concept of integrating physics-based and data-driven approaches has become popular for modeling sustainable energy systems. However, the existing literature mainly focuses on the data-driven surrogates generated to replace physics-based models. These models often trade accuracy for speed but lack the generalisability, adaptability, and interpretability inherent in physics-based models, which are often indispensable in the modeling of real-world dynamic systems for optimization and control purposes. In this work, we propose a novel architecture for generating model-integrated neural networks (MINN) to allow integration on the level of learning physics-based dynamics of the system. The obtained hybrid model solves an unsettled research problem in control-oriented modeling, i.e., how to obtain an optimally simplified model that is physically insightful, numerically accurate, and computationally tractable simultaneously. We apply the proposed neural network architecture to model the electrochemical dynamics of lithium-ion batteries and show that MINN is extremely data-efficient to train while being sufficiently generalizable to previously unseen input data, owing to its underlying physical invariants. The MINN battery model has an accuracy comparable to the first principle-based model in predicting both the system outputs and any locally distributed electrochemical behaviors but achieves two orders of magnitude reduction in the solution time.

Battery Capacity Knee Identification Using Unsupervised Time Series Segmentation

Capacity knees have been observed in experimental tests of commercial lithium-ion cells of various chemistry types under different operating conditions. Their occurrence can have a significant impact on safety and profitability in battery applications. To address concerns arising from possible knee occurrence in battery applications, this work proposes an algorithm to identify capacity knees as well as their onset from capacity fade curves. The proposed capacity knee identification algorithm is validated on both synthetic degradation data and experimental degradation data of two different battery chemistries, and is also benchmarked to the state-of-the-art knee identification algorithm in the literature. The results demonstrate that our proposed capacity knee identification algorithm could successfully identify capacity knees when the state-of-the-art knee identification algorithm failed. The results can contribute to a better understanding of capacity knees and the proposed capacity knee identification algorithm can be used to, for example, systematically evaluate the knee prediction performance of both model-based methods, and data-driven methods and facilitate better classification of retired automotive batteries from safety and profitability perspectives.

Interpretable Battery Cycle Life Range Prediction Using Early Degradation Data at Cell Level

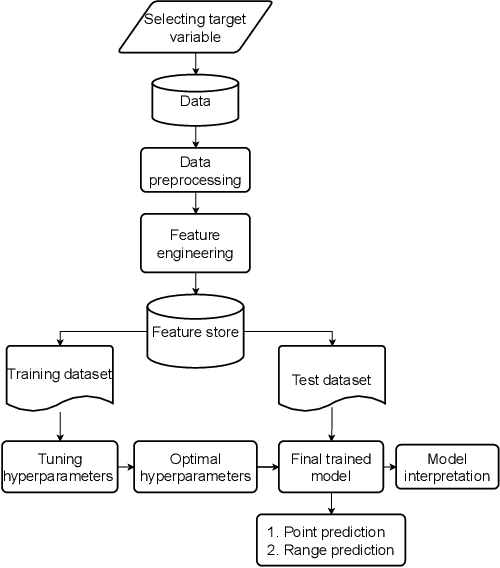
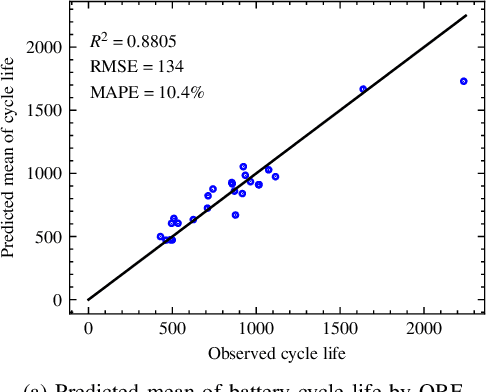
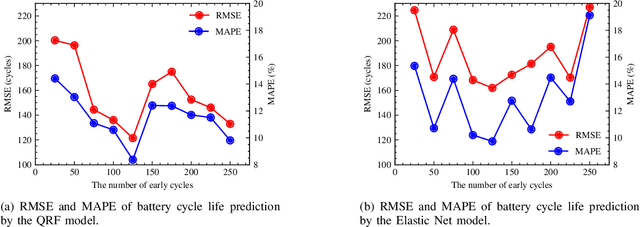
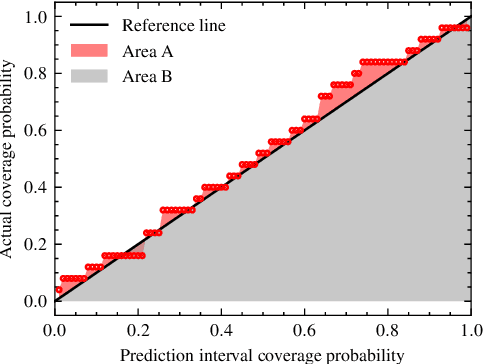
Battery cycle life prediction using early degradation data has many potential applications throughout the battery product life cycle. Various data-driven methods have been proposed for point prediction of battery cycle life with minimum knowledge of the battery degradation mechanisms. However, management of batteries at end-of-life with lower economic and technical risk requires prediction of cycle life with quantified uncertainty, which is still lacking. The interpretability (i.e., the reason for high prediction accuracy) of these advanced data-driven methods is also worthy of investigation. Here, a physics-informed Quantile Regression Forest (QRF) model is introduced to make cycle life range prediction with uncertainty quantified as the length of the prediction interval, in addition to point predictions with high accuracy. The hyperparameters of the QRF model are tuned with a proposed area-based performance evaluation metric so that the coverage probabilities associated with the prediction intervals are calibrated. The interpretability of the final QRF model is explored with two global model-agnostic methods, namely permutation importance, and partial dependence plot. The final QRF model facilitates dual-criteria decision-making to select the high-cycle-life charging protocol with consideration of both point predictions and uncertainty associated with the prediction.