Deep active learning for nonlinear system identification

The exploding research interest for neural networks in modeling nonlinear dynamical systems is largely explained by the networks' capacity to model complex input-output relations directly from data. However, they typically need vast training data before they can be put to any good use. The data generation process for dynamical systems can be an expensive endeavor both in terms of time and resources. Active learning addresses this shortcoming by acquiring the most informative data, thereby reducing the need to collect enormous datasets. What makes the current work unique is integrating the deep active learning framework into nonlinear system identification. We formulate a general static deep active learning acquisition problem for nonlinear system identification. This is enabled by exploring system dynamics locally in different regions of the input space to obtain a simulated dataset covering the broader input space. This simulated dataset can be used in a static deep active learning acquisition scheme referred to as global explorations. The global exploration acquires a batch of initial states corresponding to the most informative state-action trajectories according to a batch acquisition function. The local exploration solves an optimal control problem, finding the control trajectory that maximizes some measure of information. After a batch of informative initial states is acquired, a new round of local explorations from the initial states in the batch is conducted to obtain a set of corresponding control trajectories that are to be applied on the system dynamics to get data from the system. Information measures used in the acquisition scheme are derived from the predictive variance of an ensemble of neural networks. The novel method outperforms standard data acquisition methods used for system identification of nonlinear dynamical systems in the case study performed on simulated data.

Sparse neural networks with skip-connections for nonlinear system identification

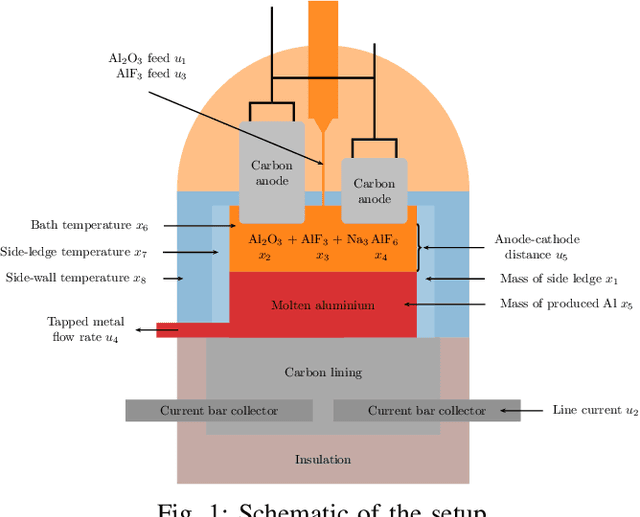
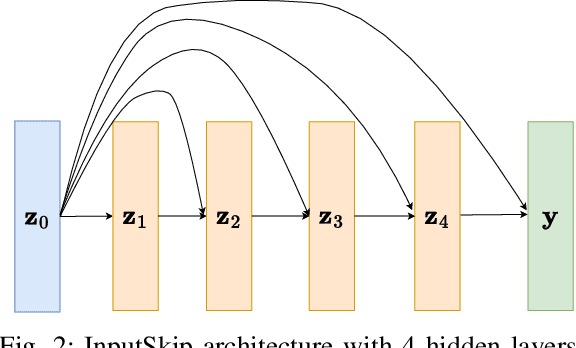
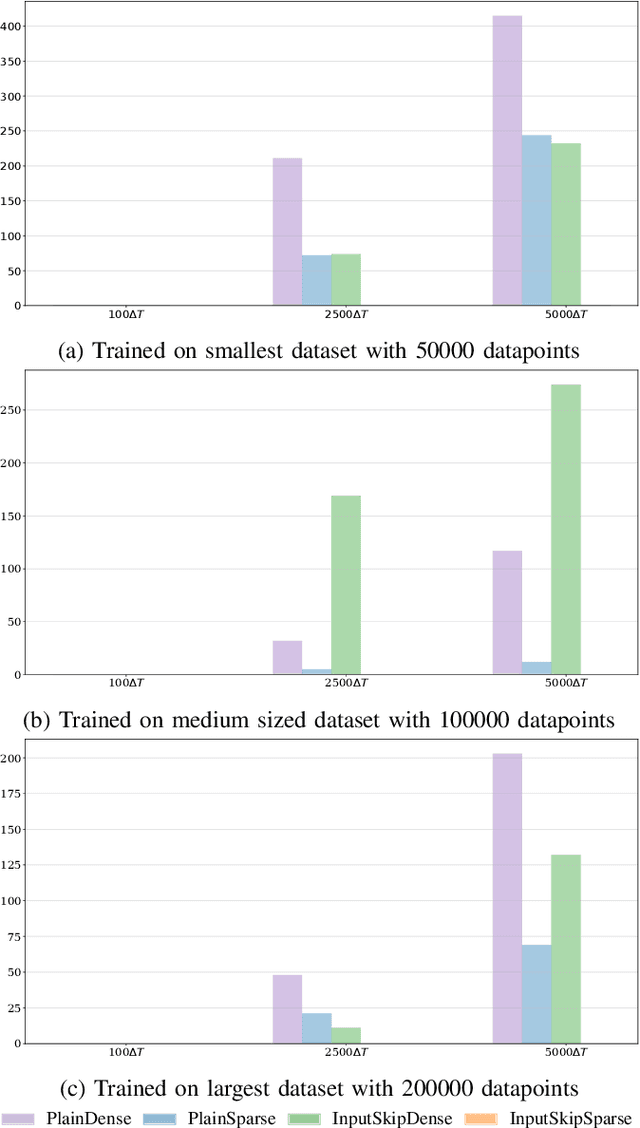
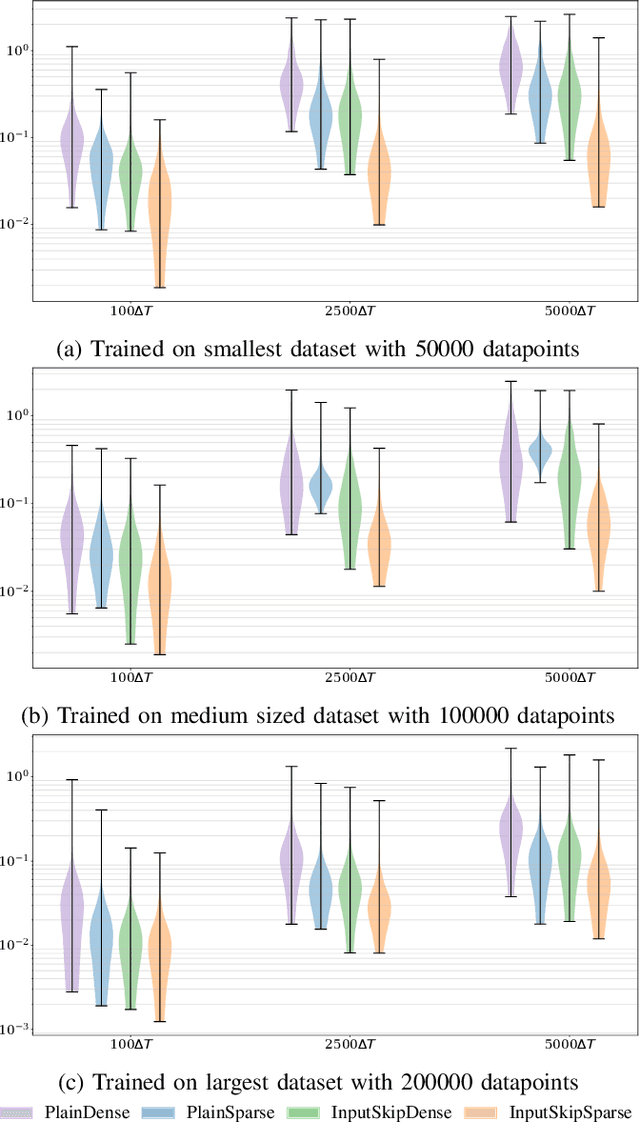
Data-driven models such as neural networks are being applied more and more to safety-critical applications, such as the modeling and control of cyber-physical systems. Despite the flexibility of the approach, there are still concerns about the safety of these models in this context, as well as the need for large amounts of potentially expensive data. In particular, when long-term predictions are needed or frequent measurements are not available, the open-loop stability of the model becomes important. However, it is difficult to make such guarantees for complex black-box models such as neural networks, and prior work has shown that model stability is indeed an issue. In this work, we consider an aluminum extraction process where measurements of the internal state of the reactor are time-consuming and expensive. We model the process using neural networks and investigate the role of including skip connections in the network architecture as well as using l1 regularization to induce sparse connection weights. We demonstrate that these measures can greatly improve both the accuracy and the stability of the models for datasets of varying sizes.

Sparse deep neural networks for modeling aluminum electrolysis dynamics

Artificial neural networks have a broad array of applications today due to their high degree of flexibility and ability to model nonlinear functions from data. However, the trustworthiness of neural networks is limited due to their black-box nature, their poor ability to generalize from small datasets, and their inconsistent convergence during training. Aluminum electrolysis is a complex nonlinear process with many interrelated sub-processes. Artificial neural networks can potentially be well suited for modeling the aluminum electrolysis process, but the safety-critical nature of this process requires trustworthy models. In this work, sparse neural networks are trained to model the system dynamics of an aluminum electrolysis simulator. The sparse model structure has a significantly reduction in model complexity compared to a corresponding dense neural network. We argue that this makes the model more interpretable. Furthermore, the empirical study shows that the sparse models generalize better from small training sets than dense neural networks. Moreover, training an ensemble of sparse neural networks with different parameter initializations show that the models converge to similar model structures with similar learned input features.