Episodic Gaussian Process-Based Learning Control with Vanishing Tracking Errors

Due to the increasing complexity of technical systems, accurate first principle models can often not be obtained. Supervised machine learning can mitigate this issue by inferring models from measurement data. Gaussian process regression is particularly well suited for this purpose due to its high data-efficiency and its explicit uncertainty representation, which allows the derivation of prediction error bounds. These error bounds have been exploited to show tracking accuracy guarantees for a variety of control approaches, but their direct dependency on the training data is generally unclear. We address this issue by deriving a Bayesian prediction error bound for GP regression, which we show to decay with the growth of a novel, kernel-based measure of data density. Based on the prediction error bound, we prove time-varying tracking accuracy guarantees for learned GP models used as feedback compensation of unknown nonlinearities, and show to achieve vanishing tracking error with increasing data density. This enables us to develop an episodic approach for learning Gaussian process models, such that an arbitrary tracking accuracy can be guaranteed. The effectiveness of the derived theory is demonstrated in several simulations.

Uniform Error and Posterior Variance Bounds for Gaussian Process Regression with Application to Safe Control

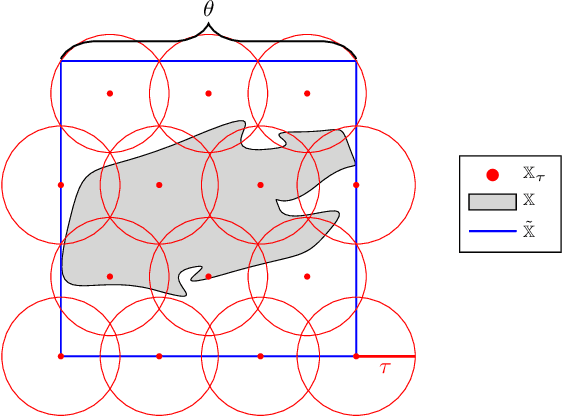
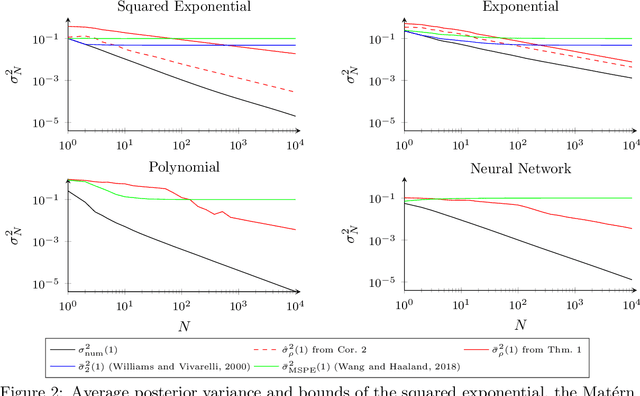
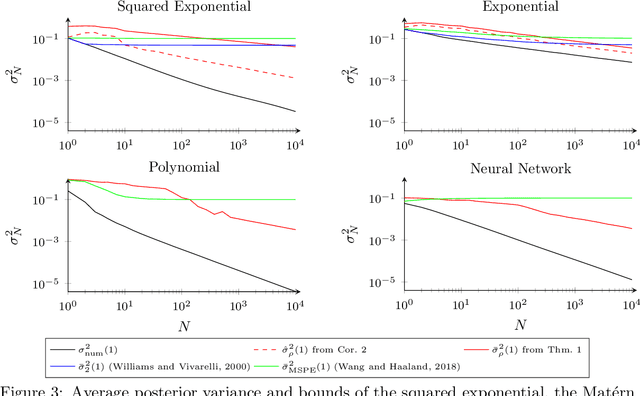
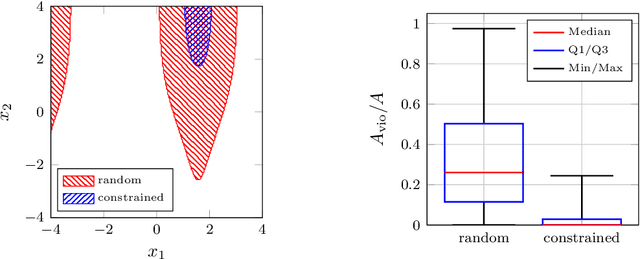
In application areas where data generation is expensive, Gaussian processes are a preferred supervised learning model due to their high data-efficiency. Particularly in model-based control, Gaussian processes allow the derivation of performance guarantees using probabilistic model error bounds. To make these approaches applicable in practice, two open challenges must be solved i) Existing error bounds rely on prior knowledge, which might not be available for many real-world tasks. (ii) The relationship between training data and the posterior variance, which mainly drives the error bound, is not well understood and prevents the asymptotic analysis. This article addresses these issues by presenting a novel uniform error bound using Lipschitz continuity and an analysis of the posterior variance function for a large class of kernels. Additionally, we show how these results can be used to guarantee safe control of an unknown dynamical system and provide numerical illustration examples.

The Value of Data in Learning-Based Control for Training Subset Selection

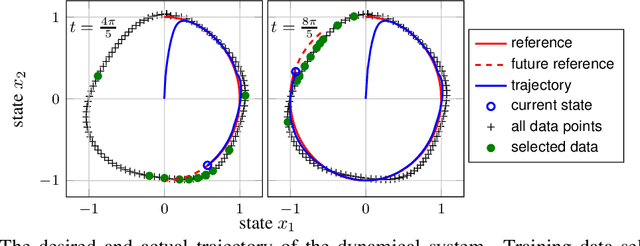
Despite the existence of formal guarantees for learning-based control approaches, the relationship between data and control performance is still poorly understood. In this paper, we present a measure to quantify the value of data within the context of a predefined control task. Our approach is applicable to a wide variety of unknown nonlinear systems that are to be controlled by a generic learning-based control law. We model the unknown component of the system using Gaussian processes, which in turn allows us to directly assess the impact of model uncertainty on control. Results obtained in numerical simulations indicate the efficacy of the proposed measure.

Real-time Uncertainty Decomposition for Online Learning Control

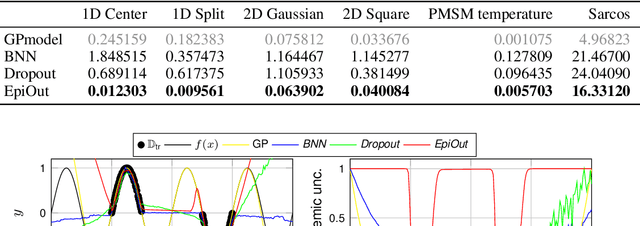
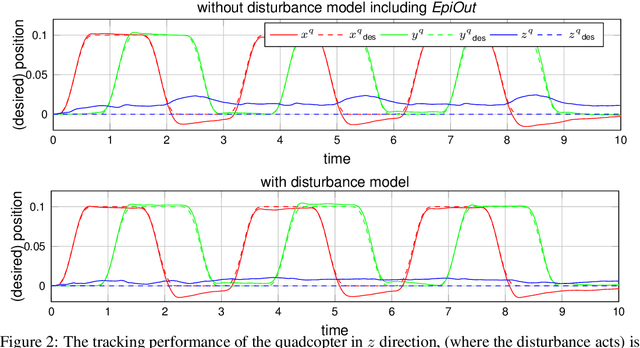
Safety-critical decisions based on machine learning models require a clear understanding of the involved uncertainties to avoid hazardous or risky situations. While aleatoric uncertainty can be explicitly modeled given a parametric description, epistemic uncertainty rather describes the presence or absence of training data. This paper proposes a novel generic method for modeling epistemic uncertainty and shows its advantages over existing approaches for neural networks on various data sets. It can be directly combined with aleatoric uncertainty estimates and allows for prediction in real-time as the inference is sample-free. We exploit this property in a model-based quadcopter control setting and demonstrate how the controller benefits from a differentiation between aleatoric and epistemic uncertainty in online learning of thermal disturbances.

Localized active learning of Gaussian process state space models

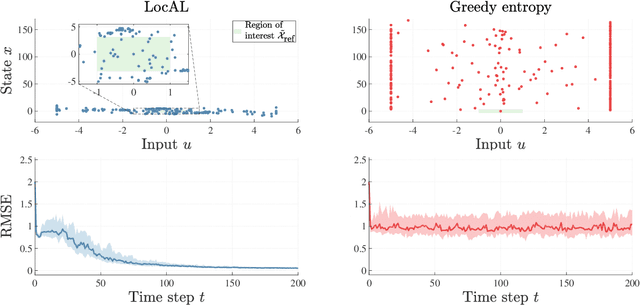
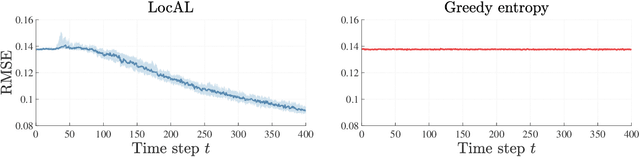
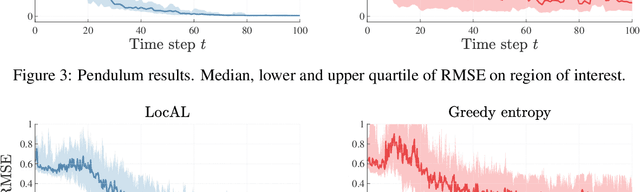
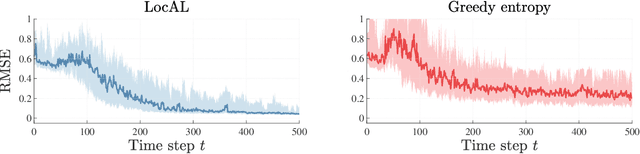
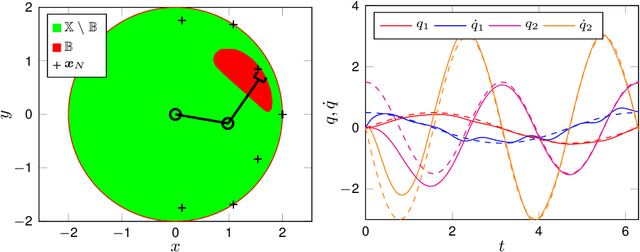
The performance of learning-based control techniques crucially depends on how effectively the system is explored. While most exploration techniques aim to achieve a globally accurate model, such approaches are generally unsuited for systems with unbounded state spaces. Furthermore, a globally accurate model is not required to achieve good performance in many common control applications, e.g., local stabilization tasks. In this paper, we propose an active learning strategy for Gaussian process state space models that aims to obtain an accurate model on a bounded subset of the state-action space. Our approach aims to maximize the mutual information of the exploration trajectories with respect to a discretization of the region of interest. By employing model predictive control, the proposed technique integrates information collected during exploration and adaptively improves its exploration strategy. To enable computational tractability, we decouple the choice of most informative data points from the model predictive control optimization step. This yields two optimization problems that can be solved in parallel. We apply the proposed method to explore the state space of various dynamical systems and compare our approach to a commonly used entropy-based exploration strategy. In all experiments, our method yields a better model within the region of interest than the entropy-based method.

How Training Data Impacts Performance in Learning-based Control

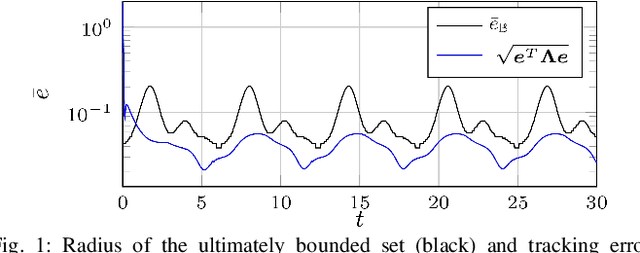
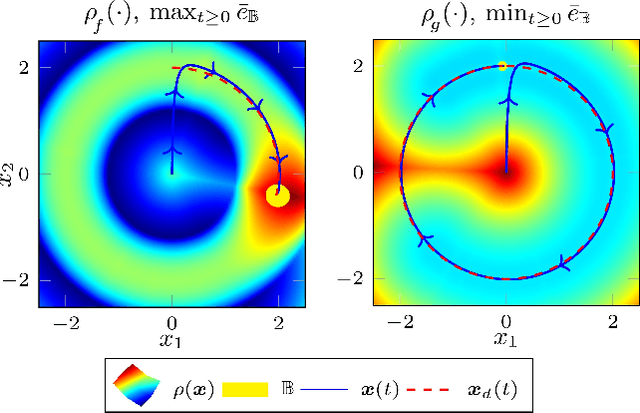
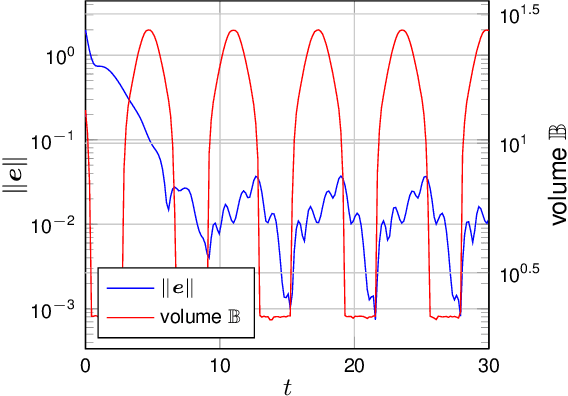
When first principle models cannot be derived due to the complexity of the real system, data-driven methods allow us to build models from system observations. As these models are employed in learning-based control, the quality of the data plays a crucial role for the performance of the resulting control law. Nevertheless, there hardly exist measures for assessing training data sets, and the impact of the distribution of the data on the closed-loop system properties is largely unknown. This paper derives - based on Gaussian process models - an analytical relationship between the density of the training data and the control performance. We formulate a quality measure for the data set, which we refer to as $\rho$-gap, and derive the ultimate bound for the tracking error under consideration of the model uncertainty. We show how the $\rho$-gap can be applied to a feedback linearizing control law and provide numerical illustrations for our approach.

Posterior Variance Analysis of Gaussian Processes with Application to Average Learning Curves

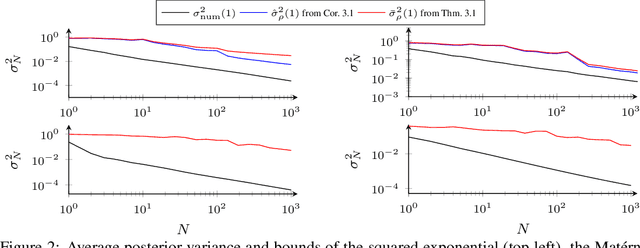
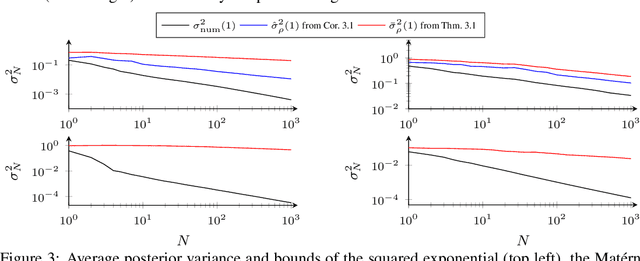
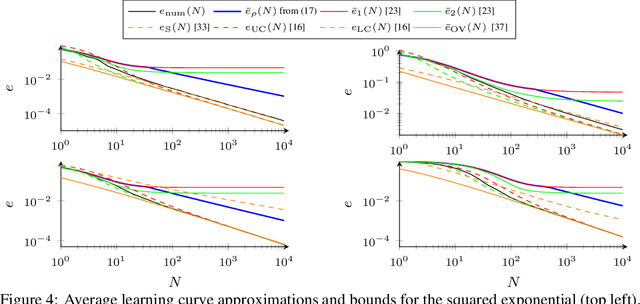
The posterior variance of Gaussian processes is a valuable measure of the learning error which is exploited in various applications such as safe reinforcement learning and control design. However, suitable analysis of the posterior variance which captures its behavior for finite and infinite number of training data is missing. This paper derives a novel bound for the posterior variance function which requires only local information because it depends only on the number of training samples in the proximity of a considered test point. Furthermore, we prove sufficient conditions which ensure the convergence of the posterior variance to zero. Finally, we demonstrate that the extension of our bound to an average learning bound outperforms existing approaches.

Uniform Error Bounds for Gaussian Process Regression with Application to Safe Control

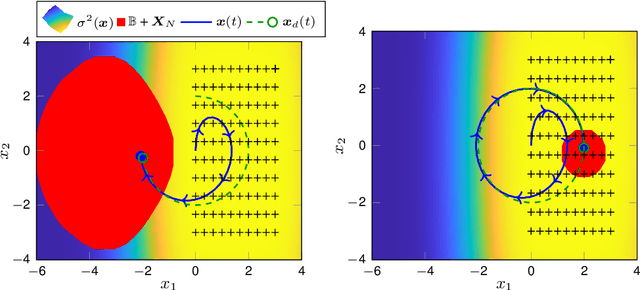
Data-driven models are subject to model errors due to limited and noisy training data. Key to the application of such models in safety-critical domains is the quantification of their model error. Gaussian processes provide such a measure and uniform error bounds have been derived, which allow safe control based on these models. However, existing error bounds require restrictive assumptions. In this paper, we employ the Gaussian process distribution and continuity arguments to derive a novel uniform error bound under weaker assumptions. Furthermore, we demonstrate how this distribution can be used to derive probabilistic Lipschitz constants and analyze the asymptotic behavior of our bound. Finally, we derive safety conditions for the control of unknown dynamical systems based on Gaussian process models and evaluate them in simulations of a robotic manipulator.

Mean Square Prediction Error of Misspecified Gaussian Process Models

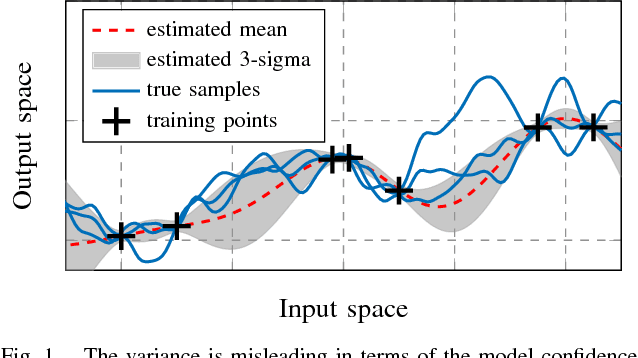
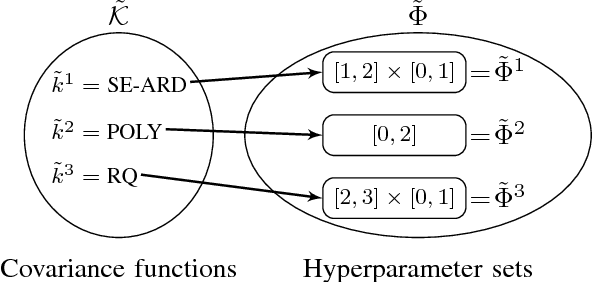
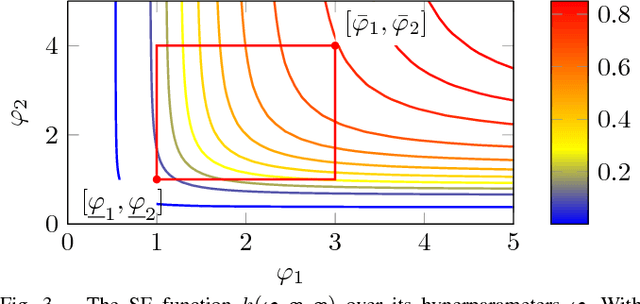
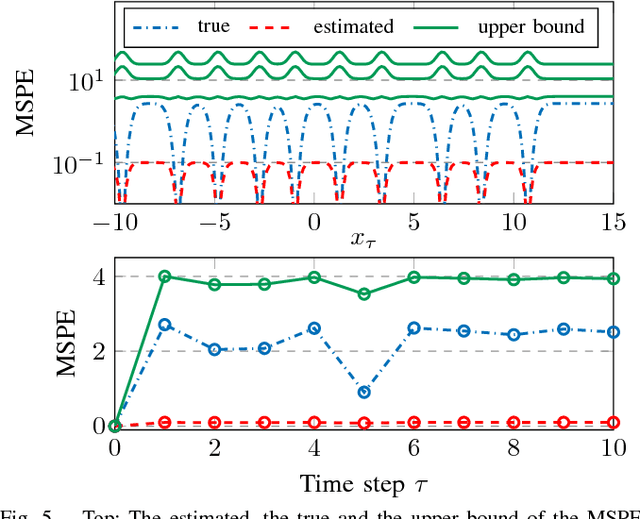
Nonparametric modeling approaches show very promising results in the area of system identification and control. A naturally provided model confidence is highly relevant for system-theoretical considerations to provide guarantees for application scenarios. Gaussian process regression represents one approach which provides such an indicator for the model confidence. However, this measure is only valid if the covariance function and its hyperparameters fit the underlying data generating process. In this paper, we derive an upper bound for the mean square prediction error of misspecified Gaussian process models based on a pseudo-concave optimization problem. We present application scenarios and a simulation to compare the derived upper bound with the true mean square error.