How Training Data Impacts Performance in Learning-based Control
Paper and Code
May 25, 2020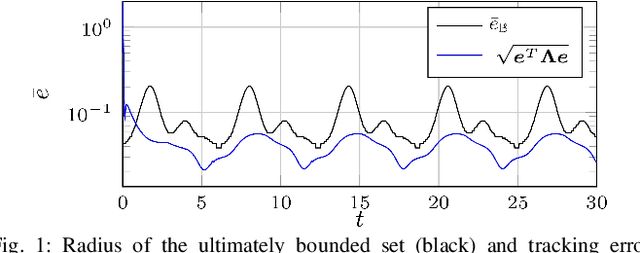
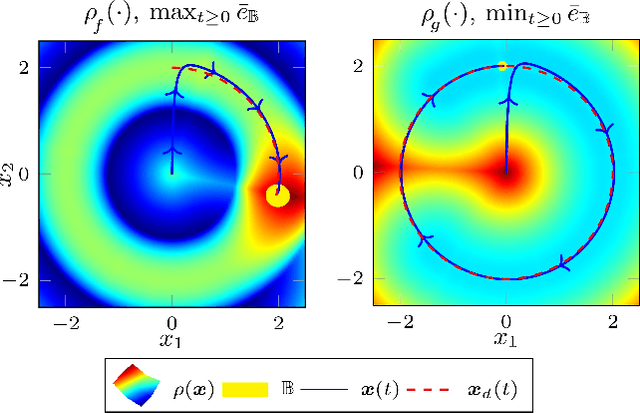
When first principle models cannot be derived due to the complexity of the real system, data-driven methods allow us to build models from system observations. As these models are employed in learning-based control, the quality of the data plays a crucial role for the performance of the resulting control law. Nevertheless, there hardly exist measures for assessing training data sets, and the impact of the distribution of the data on the closed-loop system properties is largely unknown. This paper derives - based on Gaussian process models - an analytical relationship between the density of the training data and the control performance. We formulate a quality measure for the data set, which we refer to as $\rho$-gap, and derive the ultimate bound for the tracking error under consideration of the model uncertainty. We show how the $\rho$-gap can be applied to a feedback linearizing control law and provide numerical illustrations for our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge