Uniform Error and Posterior Variance Bounds for Gaussian Process Regression with Application to Safe Control
Paper and Code
Jan 13, 2021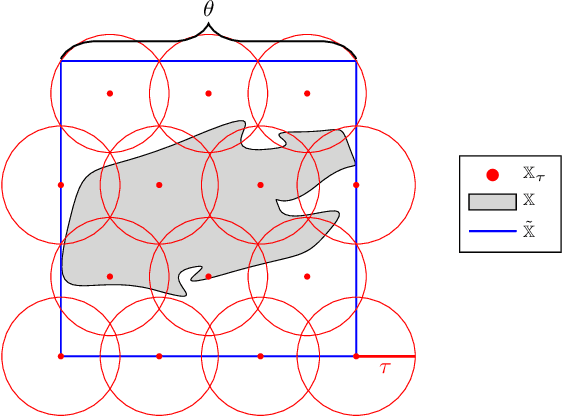
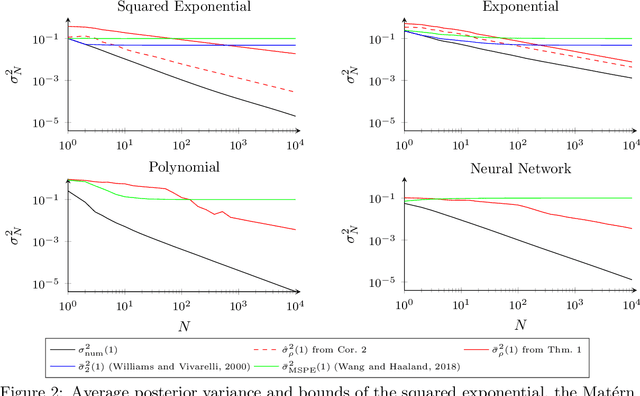
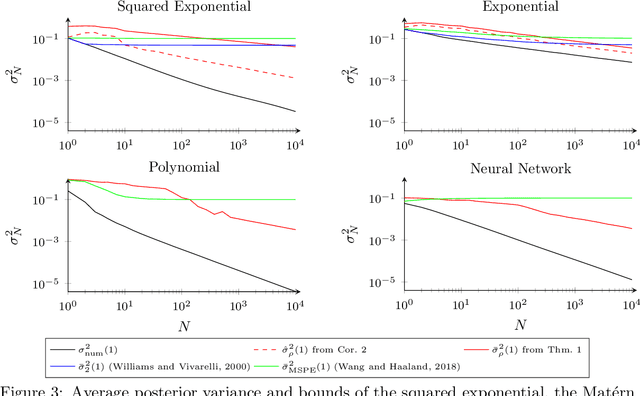
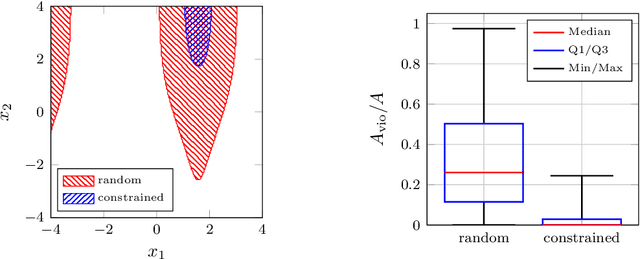
In application areas where data generation is expensive, Gaussian processes are a preferred supervised learning model due to their high data-efficiency. Particularly in model-based control, Gaussian processes allow the derivation of performance guarantees using probabilistic model error bounds. To make these approaches applicable in practice, two open challenges must be solved i) Existing error bounds rely on prior knowledge, which might not be available for many real-world tasks. (ii) The relationship between training data and the posterior variance, which mainly drives the error bound, is not well understood and prevents the asymptotic analysis. This article addresses these issues by presenting a novel uniform error bound using Lipschitz continuity and an analysis of the posterior variance function for a large class of kernels. Additionally, we show how these results can be used to guarantee safe control of an unknown dynamical system and provide numerical illustration examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge