Localized active learning of Gaussian process state space models
Paper and Code
Jun 04, 2020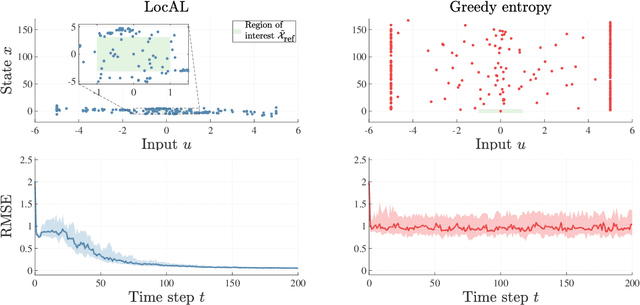
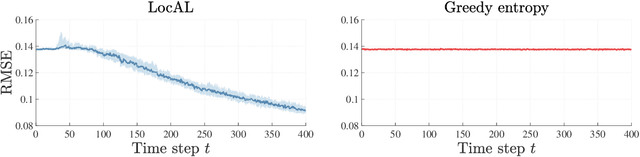
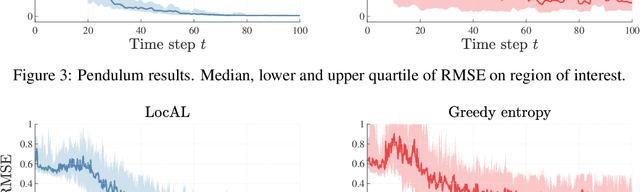
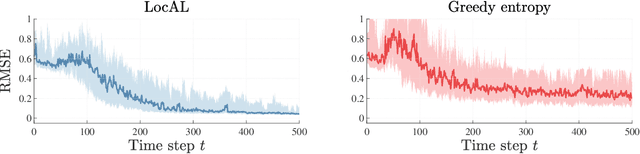
The performance of learning-based control techniques crucially depends on how effectively the system is explored. While most exploration techniques aim to achieve a globally accurate model, such approaches are generally unsuited for systems with unbounded state spaces. Furthermore, a globally accurate model is not required to achieve good performance in many common control applications, e.g., local stabilization tasks. In this paper, we propose an active learning strategy for Gaussian process state space models that aims to obtain an accurate model on a bounded subset of the state-action space. Our approach aims to maximize the mutual information of the exploration trajectories with respect to a discretization of the region of interest. By employing model predictive control, the proposed technique integrates information collected during exploration and adaptively improves its exploration strategy. To enable computational tractability, we decouple the choice of most informative data points from the model predictive control optimization step. This yields two optimization problems that can be solved in parallel. We apply the proposed method to explore the state space of various dynamical systems and compare our approach to a commonly used entropy-based exploration strategy. In all experiments, our method yields a better model within the region of interest than the entropy-based method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge