Physics-Constrained Learning for PDE Systems with Uncertainty Quantified Port-Hamiltonian Models

Modeling the dynamics of flexible objects has become an emerging topic in the community as these objects become more present in many applications, e.g., soft robotics. Due to the properties of flexible materials, the movements of soft objects are often highly nonlinear and, thus, complex to predict. Data-driven approaches seem promising for modeling those complex dynamics but often neglect basic physical principles, which consequently makes them untrustworthy and limits generalization. To address this problem, we propose a physics-constrained learning method that combines powerful learning tools and reliable physical models. Our method leverages the data collected from observations by sending them into a Gaussian process that is physically constrained by a distributed Port-Hamiltonian model. Based on the Bayesian nature of the Gaussian process, we not only learn the dynamics of the system, but also enable uncertainty quantification. Furthermore, the proposed approach preserves the compositional nature of Port-Hamiltonian systems.

Physics-enhanced Gaussian Process Variational Autoencoder

Variational autoencoders allow to learn a lower-dimensional latent space based on high-dimensional input/output data. Using video clips as input data, the encoder may be used to describe the movement of an object in the video without ground truth data (unsupervised learning). Even though the object's dynamics is typically based on first principles, this prior knowledge is mostly ignored in the existing literature. Thus, we propose a physics-enhanced variational autoencoder that places a physical-enhanced Gaussian process prior on the latent dynamics to improve the efficiency of the variational autoencoder and to allow physically correct predictions. The physical prior knowledge expressed as linear dynamical system is here reflected by the Green's function and included in the kernel function of the Gaussian process. The benefits of the proposed approach are highlighted in a simulation with an oscillating particle.

Gaussian Process Port-Hamiltonian Systems: Bayesian Learning with Physics Prior

Data-driven approaches achieve remarkable results for the modeling of complex dynamics based on collected data. However, these models often neglect basic physical principles which determine the behavior of any real-world system. This omission is unfavorable in two ways: The models are not as data-efficient as they could be by incorporating physical prior knowledge, and the model itself might not be physically correct. We propose Gaussian Process Port-Hamiltonian systems (GP-PHS) as a physics-informed Bayesian learning approach with uncertainty quantification. The Bayesian nature of GP-PHS uses collected data to form a distribution over all possible Hamiltonians instead of a single point estimate. Due to the underlying physics model, a GP-PHS generates passive systems with respect to designated inputs and outputs. Further, the proposed approach preserves the compositional nature of Port-Hamiltonian systems.

Learning Switching Port-Hamiltonian Systems with Uncertainty Quantification

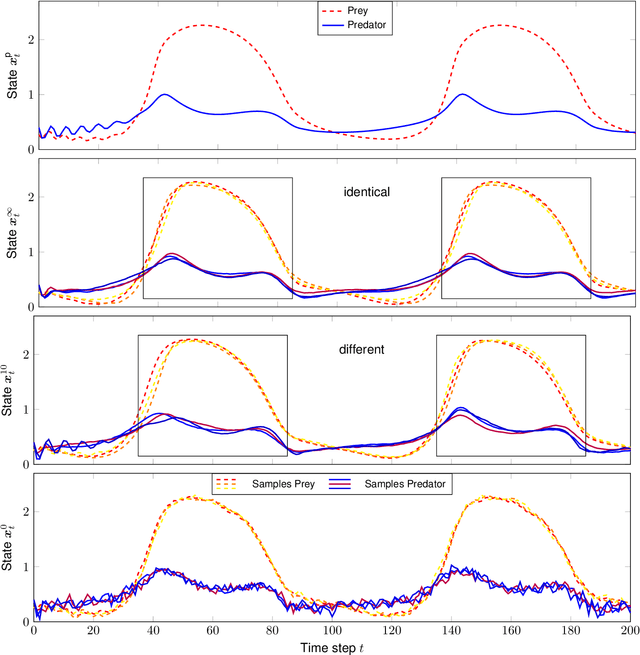
Switching physical systems are ubiquitous in modern control applications, for instance, locomotion behavior of robots and animals, power converters with switches and diodes. The dynamics and switching conditions are often hard to obtain or even inaccessible in case of a-priori unknown environments and nonlinear components. Black-box neural networks can learn to approximately represent switching dynamics, but typically require a large amount of data, neglect the underlying axioms of physics, and lack of uncertainty quantification. We propose a Gaussian process based learning approach enhanced by switching Port-Hamiltonian systems (GP-SPHS) to learn physical plausible system dynamics and identify the switching condition. The Bayesian nature of Gaussian processes uses collected data to form a distribution over all possible switching policies and dynamics that allows for uncertainty quantification. Furthermore, the proposed approach preserves the compositional nature of Port-Hamiltonian systems. A simulation with a hopping robot validates the effectiveness of the proposed approach.

The Value of Data in Learning-Based Control for Training Subset Selection

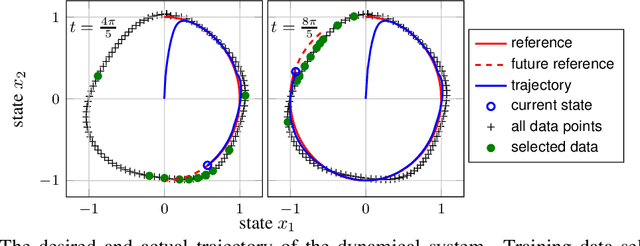
Despite the existence of formal guarantees for learning-based control approaches, the relationship between data and control performance is still poorly understood. In this paper, we present a measure to quantify the value of data within the context of a predefined control task. Our approach is applicable to a wide variety of unknown nonlinear systems that are to be controlled by a generic learning-based control law. We model the unknown component of the system using Gaussian processes, which in turn allows us to directly assess the impact of model uncertainty on control. Results obtained in numerical simulations indicate the efficacy of the proposed measure.

Real-time Uncertainty Decomposition for Online Learning Control

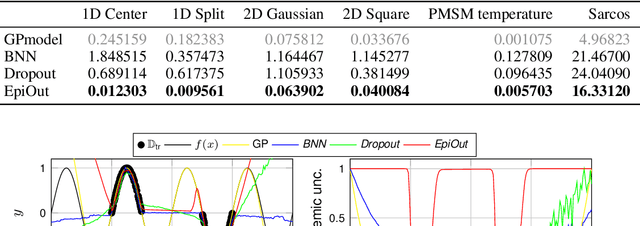
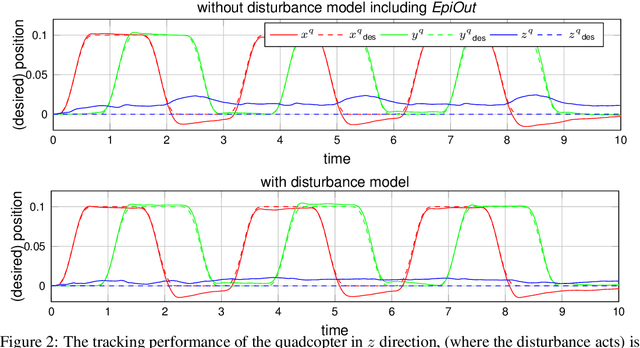
Safety-critical decisions based on machine learning models require a clear understanding of the involved uncertainties to avoid hazardous or risky situations. While aleatoric uncertainty can be explicitly modeled given a parametric description, epistemic uncertainty rather describes the presence or absence of training data. This paper proposes a novel generic method for modeling epistemic uncertainty and shows its advantages over existing approaches for neural networks on various data sets. It can be directly combined with aleatoric uncertainty estimates and allows for prediction in real-time as the inference is sample-free. We exploit this property in a model-based quadcopter control setting and demonstrate how the controller benefits from a differentiation between aleatoric and epistemic uncertainty in online learning of thermal disturbances.

Safe learning-based trajectory tracking for underactuated vehicles with partially unknown dynamics

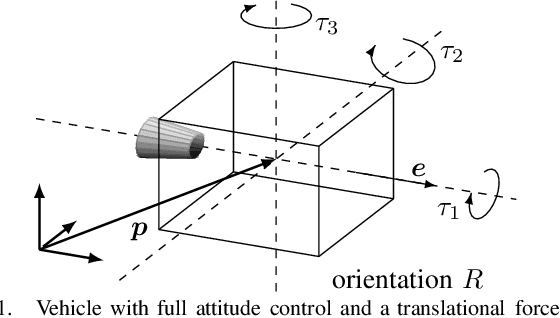
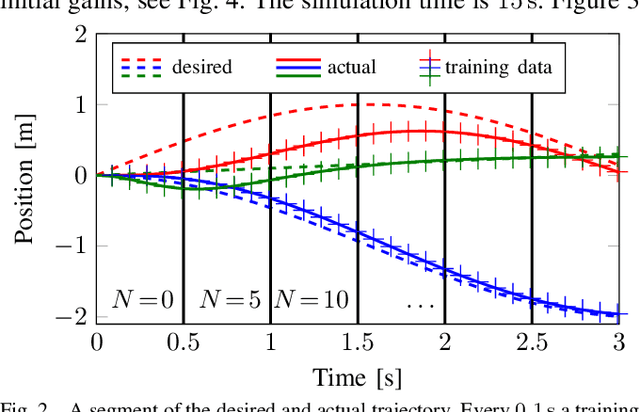
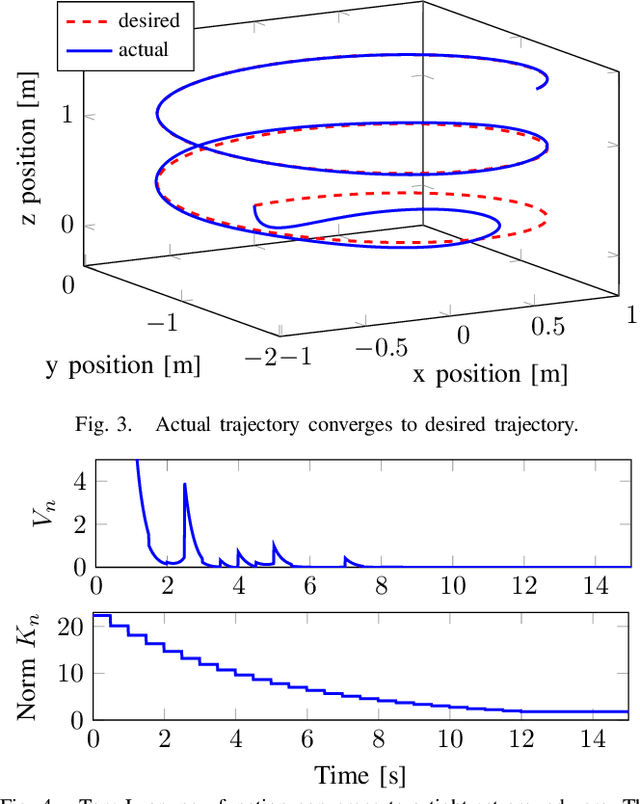
Underactuated vehicles have gained much attention in the recent years due to the increasing amount of aerial and underwater vehicles as well as nanosatellites. The safe tracking control of these vehicles is a substantial aspect for an increasing range of application domains. However, external disturbances and parts of the internal dynamics are often unknown or very time-consuming to model. To overcome this issue, we present a safe tracking control law for underactuated vehicles using a learning-based oracle for the prediction of the unknown dynamics. The presented approach guarantees the boundedness of the tracking error with high probability where the bound is explicitly given. With additional assumptions, asymptotic stability is achieved. A simulation with a quadrocopter visualizes the effectiveness of the proposed control law.

Prediction with Gaussian Process Dynamical Models

The modeling and simulation of dynamical systems is a necessary step for many control approaches. Using classical, parameter-based techniques for modeling of modern systems, e.g., soft robotics or human-robot interaction, is often challenging or even infeasible due to the complexity of the system dynamics. In contrast, data-driven approaches need only a minimum of prior knowledge and scale with the complexity of the system. In particular, Gaussian process dynamical models (GPDMs) provide very promising results for the modeling of complex dynamics. However, the control properties of these GP models are just sparsely researched, which leads to a "blackbox" treatment in modeling and control scenarios. In addition, the sampling of GPDMs for prediction purpose respecting their non-parametric nature results in non-Markovian dynamics making the theoretical analysis challenging. In this article, we present the relation of the sampling procedure and non-Markovian dynamics for two types of GPDMs and analyze the control theoretical properties focusing on the transfer between common sampling approximations. The outcomes are illustrated with numerical examples and discussed with respect to the application in control settings.

Localized active learning of Gaussian process state space models

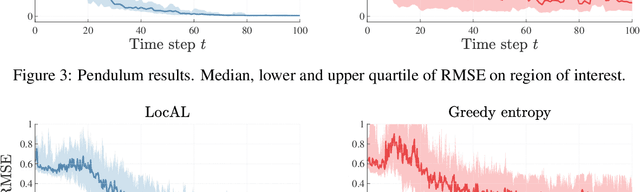
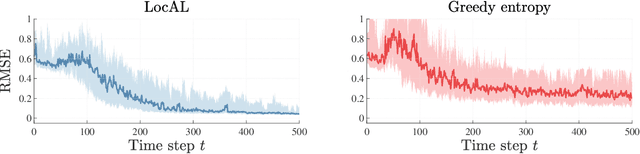
The performance of learning-based control techniques crucially depends on how effectively the system is explored. While most exploration techniques aim to achieve a globally accurate model, such approaches are generally unsuited for systems with unbounded state spaces. Furthermore, a globally accurate model is not required to achieve good performance in many common control applications, e.g., local stabilization tasks. In this paper, we propose an active learning strategy for Gaussian process state space models that aims to obtain an accurate model on a bounded subset of the state-action space. Our approach aims to maximize the mutual information of the exploration trajectories with respect to a discretization of the region of interest. By employing model predictive control, the proposed technique integrates information collected during exploration and adaptively improves its exploration strategy. To enable computational tractability, we decouple the choice of most informative data points from the model predictive control optimization step. This yields two optimization problems that can be solved in parallel. We apply the proposed method to explore the state space of various dynamical systems and compare our approach to a commonly used entropy-based exploration strategy. In all experiments, our method yields a better model within the region of interest than the entropy-based method.

Closed-loop Model Selection for Kernel-based Models using Bayesian Optimization

Kernel-based nonparametric models have become very attractive for model-based control approaches for nonlinear systems. However, the selection of the kernel and its hyperparameters strongly influences the quality of the learned model. Classically, these hyperparameters are optimized to minimize the prediction error of the model but this process totally neglects its later usage in the control loop. In this work, we present a framework to optimize the kernel and hyperparameters of a kernel-based model directly with respect to the closed-loop performance of the model. Our framework uses Bayesian optimization to iteratively refine the kernel-based model using the observed performance on the actual system until a desired performance is achieved. We demonstrate the proposed approach in a simulation and on a 3-DoF robotic arm.