Prediction with Gaussian Process Dynamical Models

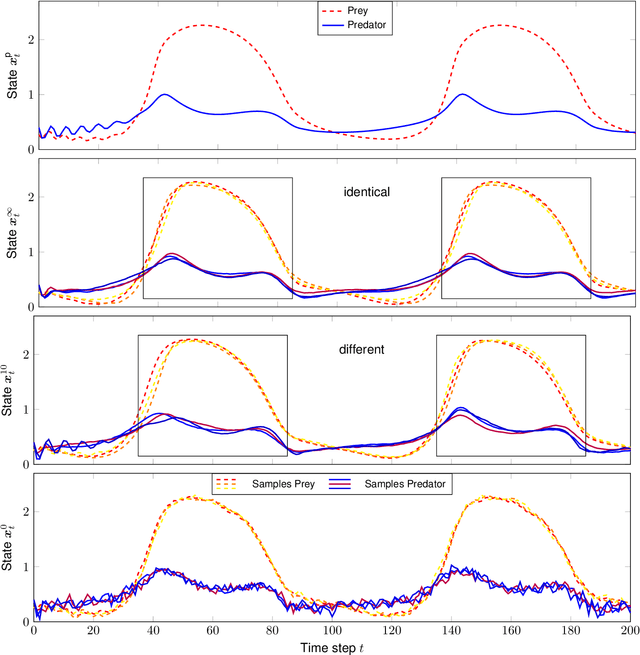
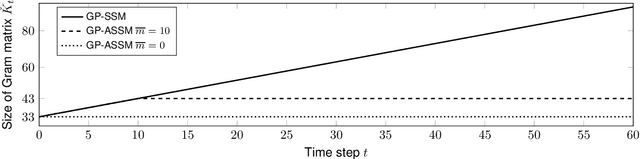
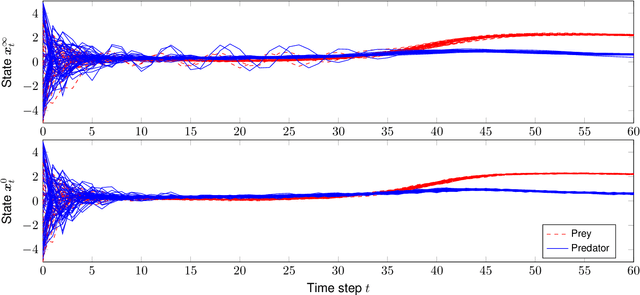
The modeling and simulation of dynamical systems is a necessary step for many control approaches. Using classical, parameter-based techniques for modeling of modern systems, e.g., soft robotics or human-robot interaction, is often challenging or even infeasible due to the complexity of the system dynamics. In contrast, data-driven approaches need only a minimum of prior knowledge and scale with the complexity of the system. In particular, Gaussian process dynamical models (GPDMs) provide very promising results for the modeling of complex dynamics. However, the control properties of these GP models are just sparsely researched, which leads to a "blackbox" treatment in modeling and control scenarios. In addition, the sampling of GPDMs for prediction purpose respecting their non-parametric nature results in non-Markovian dynamics making the theoretical analysis challenging. In this article, we present the relation of the sampling procedure and non-Markovian dynamics for two types of GPDMs and analyze the control theoretical properties focusing on the transfer between common sampling approximations. The outcomes are illustrated with numerical examples and discussed with respect to the application in control settings.