Knowledge-based Neural Ordinary Differential Equations for Cosserat Rod-based Soft Robots

Soft robots have many advantages over rigid robots thanks to their compliant and passive nature. However, it is generally challenging to model the dynamics of soft robots due to their high spatial dimensionality, making it difficult to use model-based methods to accurately control soft robots. It often requires direct numerical simulation of partial differential equations to simulate soft robots. This not only requires an accurate numerical model, but also makes soft robot modeling slow and expensive. Deep learning algorithms have shown promises in data-driven modeling of soft robots. However, these algorithms usually require a large amount of data, which are difficult to obtain in either simulation or real-world experiments of soft robots. In this work, we propose KNODE-Cosserat, a framework that combines first-principle physics models and neural ordinary differential equations. We leverage the best from both worlds -- the generalization ability of physics-based models and the fast speed of deep learning methods. We validate our framework in both simulation and real-world experiments. In both cases, we show that the robot model significantly improves over the baseline models under different metrics.

Learning Switching Port-Hamiltonian Systems with Uncertainty Quantification

Switching physical systems are ubiquitous in modern control applications, for instance, locomotion behavior of robots and animals, power converters with switches and diodes. The dynamics and switching conditions are often hard to obtain or even inaccessible in case of a-priori unknown environments and nonlinear components. Black-box neural networks can learn to approximately represent switching dynamics, but typically require a large amount of data, neglect the underlying axioms of physics, and lack of uncertainty quantification. We propose a Gaussian process based learning approach enhanced by switching Port-Hamiltonian systems (GP-SPHS) to learn physical plausible system dynamics and identify the switching condition. The Bayesian nature of Gaussian processes uses collected data to form a distribution over all possible switching policies and dynamics that allows for uncertainty quantification. Furthermore, the proposed approach preserves the compositional nature of Port-Hamiltonian systems. A simulation with a hopping robot validates the effectiveness of the proposed approach.

Leveraging Predictive Models for Adaptive Sampling of Spatiotemporal Fluid Processes

Persistent monitoring of a spatiotemporal fluid process requires data sampling and predictive modeling of the process being monitored. In this paper we present PASST algorithm: Predictive-model based Adaptive Sampling of a Spatio-Temporal process. PASST is an adaptive robotic sampling algorithm that leverages predictive models to efficiently and persistently monitor a fluid process in a given region of interest. Our algorithm makes use of the predictions from a learned prediction model to plan a path for an autonomous vehicle to adaptively and efficiently survey the region of interest. In turn, the sampled data is used to obtain better predictions by giving an updated initial state to the predictive model. For predictive model, we use Knowledged-based Neural Ordinary Differential Equations to train models of fluid processes. These models are orders of magnitude smaller in size and run much faster than fluid data obtained from direct numerical simulations of the partial differential equations that describe the fluid processes or other comparable computational fluids models. For path planning, we use reinforcement learning based planning algorithms that use the field predictions as reward functions. We evaluate our adaptive sampling path planning algorithm on both numerically simulated fluid data and real-world nowcast ocean flow data to show that we can sample the spatiotemporal field in the given region of interest for long time horizons. We also evaluate PASST algorithm's generalization ability to sample from fluid processes that are not in the training repertoire of the learned models.

Online Dynamics Learning for Predictive Control with an Application to Aerial Robots

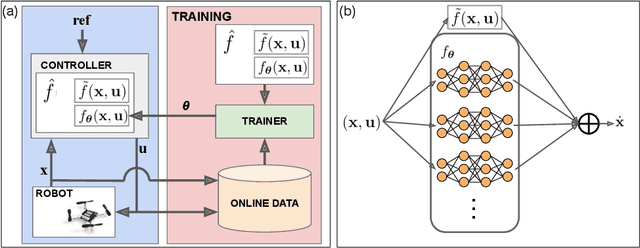
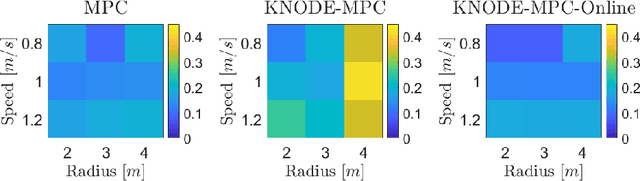
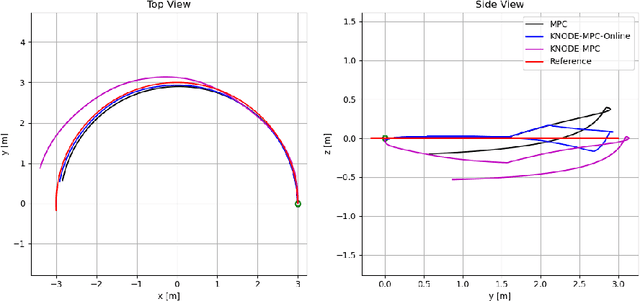
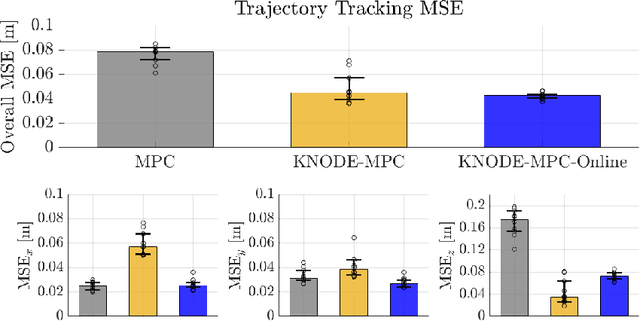
In this work, we consider the task of improving the accuracy of dynamic models for model predictive control (MPC) in an online setting. Even though prediction models can be learned and applied to model-based controllers, these models are often learned offline. In this offline setting, training data is first collected and a prediction model is learned through an elaborated training procedure. After the model is trained to a desired accuracy, it is then deployed in a model predictive controller. However, since the model is learned offline, it does not adapt to disturbances or model errors observed during deployment. To improve the adaptiveness of the model and the controller, we propose an online dynamics learning framework that continually improves the accuracy of the dynamic model during deployment. We adopt knowledge-based neural ordinary differential equations (KNODE) as the dynamic models, and use techniques inspired by transfer learning to continually improve the model accuracy. We demonstrate the efficacy of our framework with a quadrotor robot, and verify the framework in both simulations and physical experiments. Results show that the proposed approach is able to account for disturbances that are possibly time-varying, while maintaining good trajectory tracking performance.

Learning to Swarm with Knowledge-Based Neural Ordinary Differential Equations

Understanding single-agent dynamics from collective behaviors in natural swarms is crucial for informing robot controller designs in artificial swarms and multiagent robotic systems. However, the complexity in agent-to-agent interactions and the decentralized nature of most swarms pose a significant challenge to the extraction of single-robot control laws from global behavior. In this work, we consider the important task of learning decentralized single-robot controllers based solely on the state observations of a swarm's trajectory. We present a general framework by adopting knowledge-based neural ordinary differential equations (KNODE) -- a hybrid machine learning method capable of combining artificial neural networks with known agent dynamics. Our approach distinguishes itself from most prior works in that we do not require action data for learning. We apply our framework to two different flocking swarms in 2D and 3D respectively, and demonstrate efficient training by leveraging the graphical structure of the swarms' information network. We further show that the learnt single-robot controllers can not only reproduce flocking behavior in the original swarm but also scale to swarms with more robots.

KNODE-MPC: A Knowledge-based Data-driven Predictive Control Framework for Aerial Robots

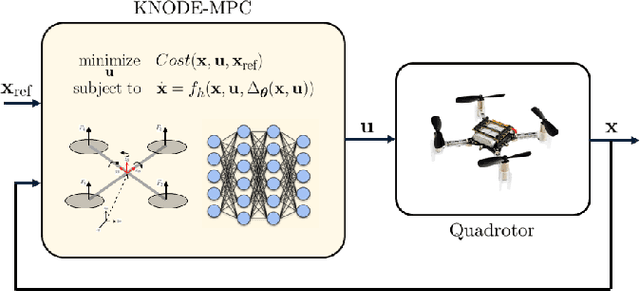
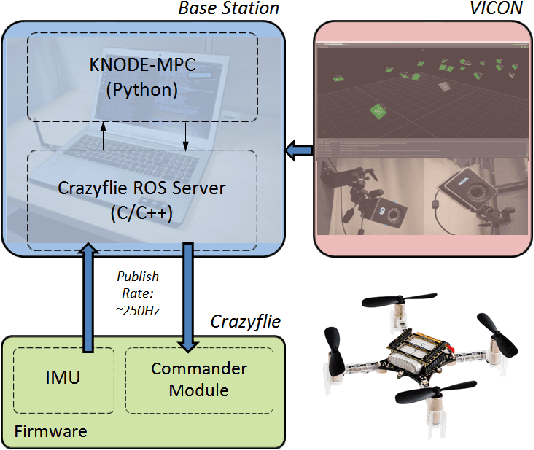
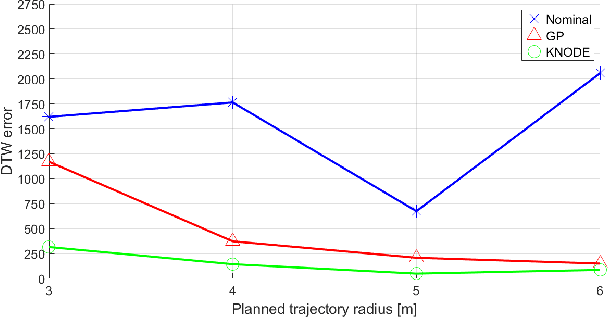
In this work, we consider the problem of deriving and incorporating accurate dynamic models for model predictive control (MPC) with an application to quadrotor control. MPC relies on precise dynamic models to achieve the desired closed-loop performance. However, the presence of uncertainties in complex systems and the environments they operate in poses a challenge in obtaining sufficiently accurate representations of the system dynamics. In this work, we make use of a deep learning tool, knowledge-based neural ordinary differential equations (KNODE), to augment a model obtained from first principles. The resulting hybrid model encompasses both a nominal first-principle model and a neural network learnt from simulated or real-world experimental data. Using a quadrotor, we benchmark our hybrid model against a state-of-the-art Gaussian Process (GP) model and show that the hybrid model provides more accurate predictions of the quadrotor dynamics and is able to generalize beyond the training data. To improve closed-loop performance, the hybrid model is integrated into a novel MPC framework, known as KNODE-MPC. Results show that the integrated framework achieves 73% improvement in simulations and more than 14% in physical experiments, in terms of trajectory tracking performance.

Deformable Image Registration using Neural ODEs

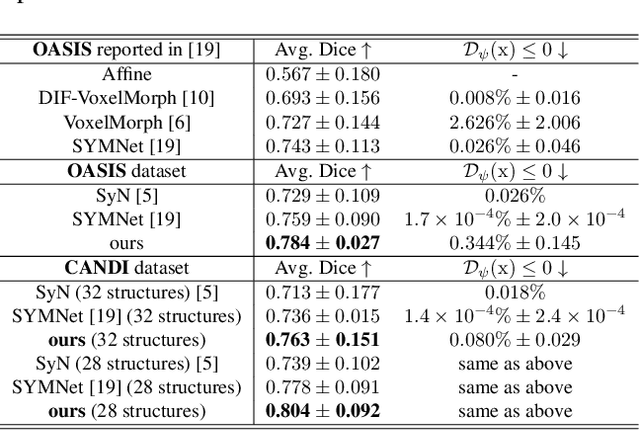
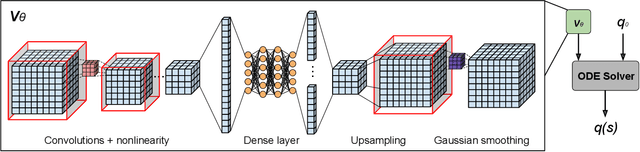
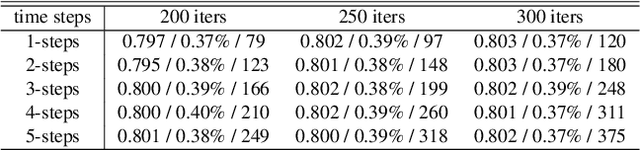
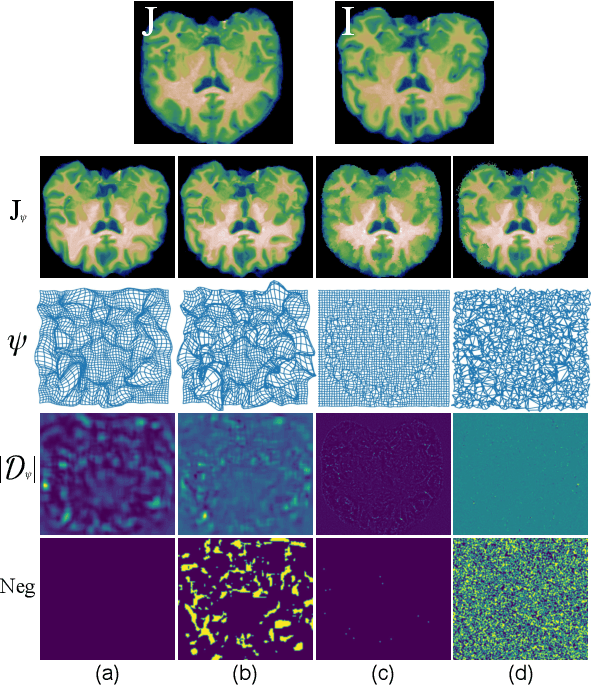
Deformable image registration, aiming to find spatial correspondence between a given image pair, is one of the most critical problems in the domain of medical image analysis. In this paper, we present a generic, fast, and accurate diffeomorphic image registration framework that leverages neural ordinary differential equations (NODEs). We model each voxel as a moving particle and consider the set of all voxels in a 3D image as a high-dimensional dynamical system whose trajectory determines the targeted deformation field. Compared with traditional optimization-based methods, our framework reduces the running time from tens of minutes to tens of seconds. Compared with recent data-driven deep learning methods, our framework is more accessible since it does not require large amounts of training data. Our experiments show that the registration results of our method outperform state-of-the-arts under various metrics, indicating that our modeling approach is well fitted for the task of deformable image registration.

Learning Nonlinear Dynamics and Chaos: A Universal Framework for Knowledge-Based System Identification and Prediction

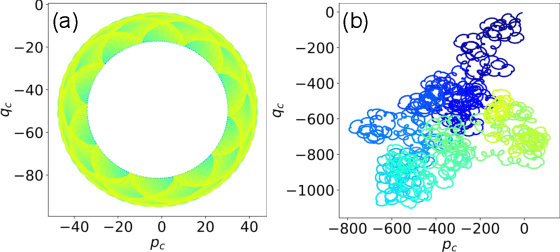
We present a universal framework for learning the behavior of dynamical systems from observations. We formulate the learning task as a constrained optimization problem which can be efficiently solved with the adjoint sensitivity method. Our scheme is flexible with regards to the choice of model, and existing knowledge can be readily incorporated for hybrid learning. We demonstrate the effectiveness of our scheme by learning a variety of systems including a stiff Van der Pol oscillator, a chaotic Lorenz system, and the Kuramoto-Sivashinsky equation. We also include examples of hybrid learning and learning from noisy observations.