Flying Quadrotors in Tight Formations using Learning-based Model Predictive Control

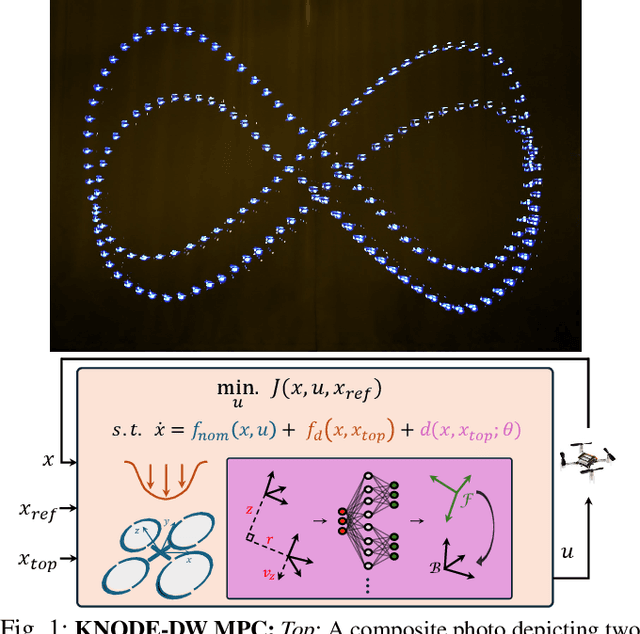
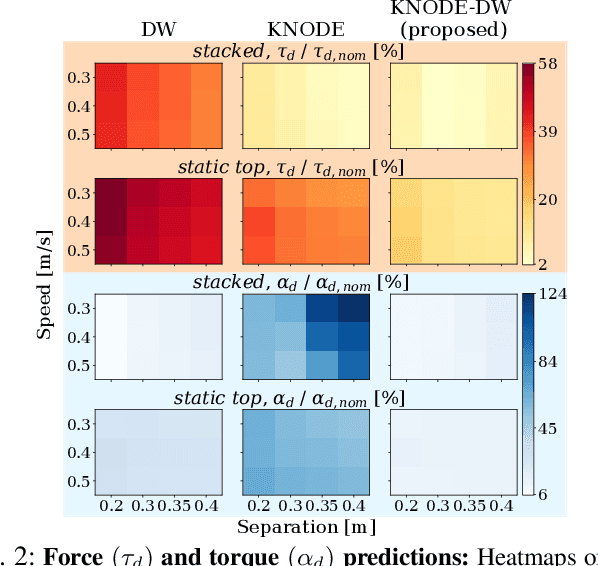
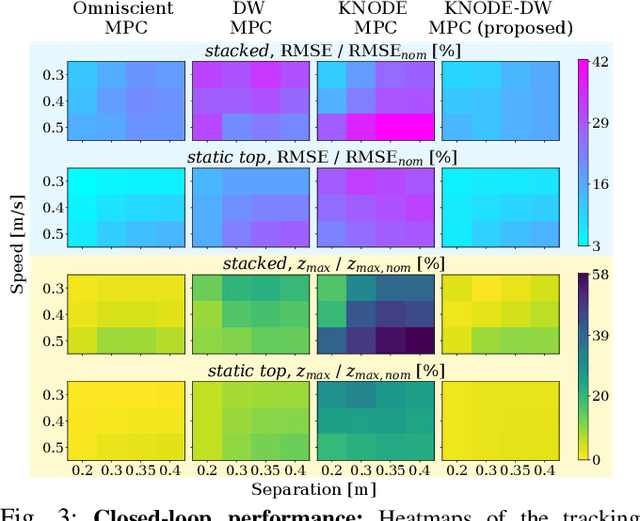
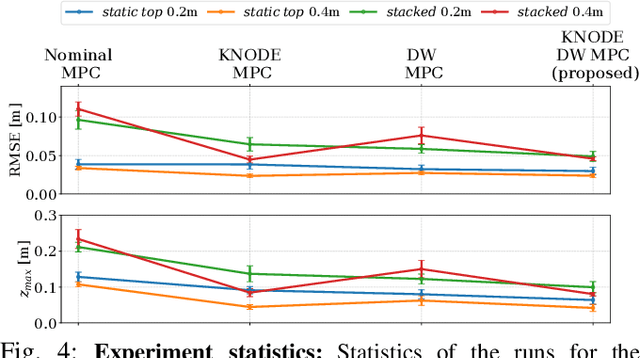
Flying quadrotors in tight formations is a challenging problem. It is known that in the near-field airflow of a quadrotor, the aerodynamic effects induced by the propellers are complex and difficult to characterize. Although machine learning tools can potentially be used to derive models that capture these effects, these data-driven approaches can be sample inefficient and the resulting models often do not generalize as well as their first-principles counterparts. In this work, we propose a framework that combines the benefits of first-principles modeling and data-driven approaches to construct an accurate and sample efficient representation of the complex aerodynamic effects resulting from quadrotors flying in formation. The data-driven component within our model is lightweight, making it amenable for optimization-based control design. Through simulations and physical experiments, we show that incorporating the model into a novel learning-based nonlinear model predictive control (MPC) framework results in substantial performance improvements in terms of trajectory tracking and disturbance rejection. In particular, our framework significantly outperforms nominal MPC in physical experiments, achieving a 40.1% improvement in the average trajectory tracking errors and a 57.5% reduction in the maximum vertical separation errors. Our framework also achieves exceptional sample efficiency, using only a total of 46 seconds of flight data for training across both simulations and physical experiments. Furthermore, with our proposed framework, the quadrotors achieve an exceptionally tight formation, flying with an average separation of less than 1.5 body lengths throughout the flight. A video illustrating our framework and physical experiments is given here: https://youtu.be/Hv-0JiVoJGo

Safety Filter Design for Neural Network Systems via Convex Optimization

With the increase in data availability, it has been widely demonstrated that neural networks (NN) can capture complex system dynamics precisely in a data-driven manner. However, the architectural complexity and nonlinearity of the NNs make it challenging to synthesize a provably safe controller. In this work, we propose a novel safety filter that relies on convex optimization to ensure safety for a NN system, subject to additive disturbances that are capable of capturing modeling errors. Our approach leverages tools from NN verification to over-approximate NN dynamics with a set of linear bounds, followed by an application of robust linear MPC to search for controllers that can guarantee robust constraint satisfaction. We demonstrate the efficacy of the proposed framework numerically on a nonlinear pendulum system.

Enhancing Sample Efficiency and Uncertainty Compensation in Learning-based Model Predictive Control for Aerial Robots

The recent increase in data availability and reliability has led to a surge in the development of learning-based model predictive control (MPC) frameworks for robot systems. Despite attaining substantial performance improvements over their non-learning counterparts, many of these frameworks rely on an offline learning procedure to synthesize a dynamics model. This implies that uncertainties encountered by the robot during deployment are not accounted for in the learning process. On the other hand, learning-based MPC methods that learn dynamics models online are computationally expensive and often require a significant amount of data. To alleviate these shortcomings, we propose a novel learning-enhanced MPC framework that incorporates components from $\mathcal{L}_1$ adaptive control into learning-based MPC. This integration enables the accurate compensation of both matched and unmatched uncertainties in a sample-efficient way, enhancing the control performance during deployment. In our proposed framework, we present two variants and apply them to the control of a quadrotor system. Through simulations and physical experiments, we demonstrate that the proposed framework not only allows the synthesis of an accurate dynamics model on-the-fly, but also significantly improves the closed-loop control performance under a wide range of spatio-temporal uncertainties.

Learning-enhanced Nonlinear Model Predictive Control using Knowledge-based Neural Ordinary Differential Equations and Deep Ensembles

Nonlinear model predictive control (MPC) is a flexible and increasingly popular framework used to synthesize feedback control strategies that can satisfy both state and control input constraints. In this framework, an optimization problem, subjected to a set of dynamics constraints characterized by a nonlinear dynamics model, is solved at each time step. Despite its versatility, the performance of nonlinear MPC often depends on the accuracy of the dynamics model. In this work, we leverage deep learning tools, namely knowledge-based neural ordinary differential equations (KNODE) and deep ensembles, to improve the prediction accuracy of this model. In particular, we learn an ensemble of KNODE models, which we refer to as the KNODE ensemble, to obtain an accurate prediction of the true system dynamics. This learned model is then integrated into a novel learning-enhanced nonlinear MPC framework. We provide sufficient conditions that guarantees asymptotic stability of the closed-loop system and show that these conditions can be implemented in practice. We show that the KNODE ensemble provides more accurate predictions and illustrate the efficacy and closed-loop performance of the proposed nonlinear MPC framework using two case studies.

LEARNEST: LEARNing Enhanced Model-based State ESTimation for Robots using Knowledge-based Neural Ordinary Differential Equations

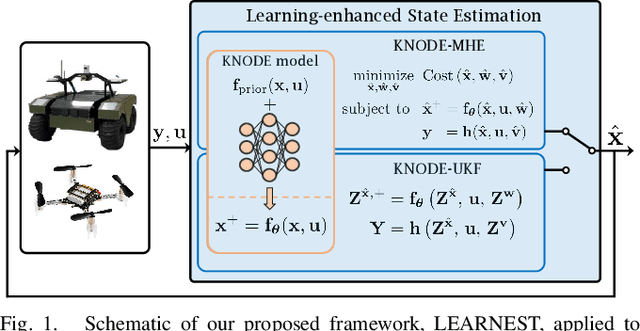
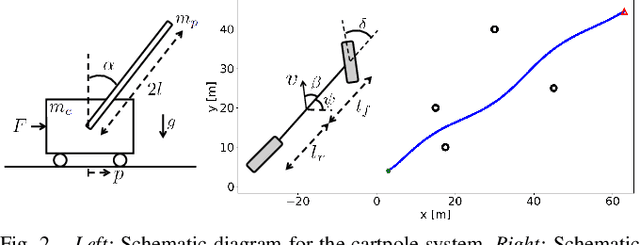
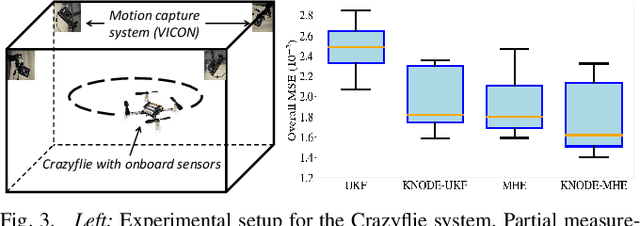
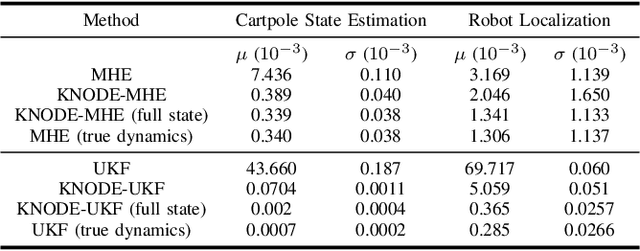
State estimation is an important aspect in many robotics applications. In this work, we consider the task of obtaining accurate state estimates for robotic systems by enhancing the dynamics model used in state estimation algorithms. Existing frameworks such as moving horizon estimation (MHE) and the unscented Kalman filter (UKF) provide the flexibility to incorporate nonlinear dynamics and measurement models. However, this implies that the dynamics model within these algorithms has to be sufficiently accurate in order to warrant the accuracy of the state estimates. To enhance the dynamics models and improve the estimation accuracy, we utilize a deep learning framework known as knowledge-based neural ordinary differential equations (KNODEs). The KNODE framework embeds prior knowledge into the training procedure and synthesizes an accurate hybrid model by fusing a prior first-principles model with a neural ordinary differential equation (NODE) model. In our proposed LEARNEST framework, we integrate the data-driven model into two novel model-based state estimation algorithms, which are denoted as KNODE-MHE and KNODE-UKF. These two algorithms are compared against their conventional counterparts across a number of robotic applications; state estimation for a cartpole system using partial measurements, localization for a ground robot, as well as state estimation for a quadrotor. Through simulations and tests using real-world experimental data, we demonstrate the versatility and efficacy of the proposed learning-enhanced state estimation framework.

Online Dynamics Learning for Predictive Control with an Application to Aerial Robots

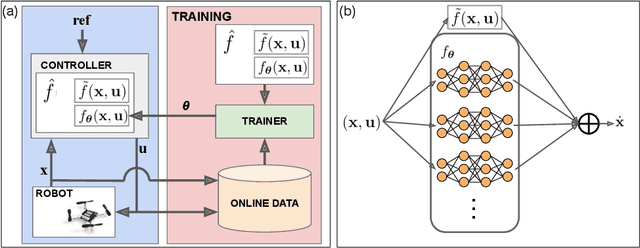
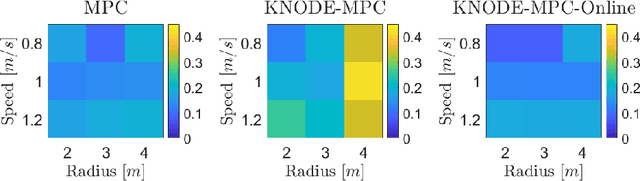
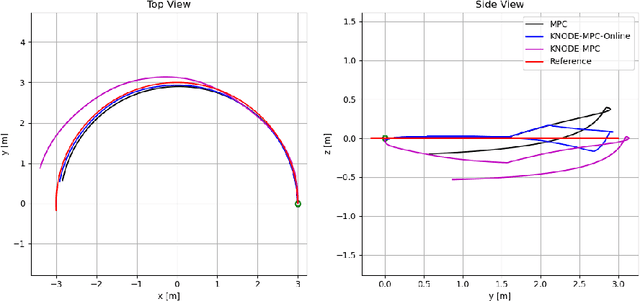
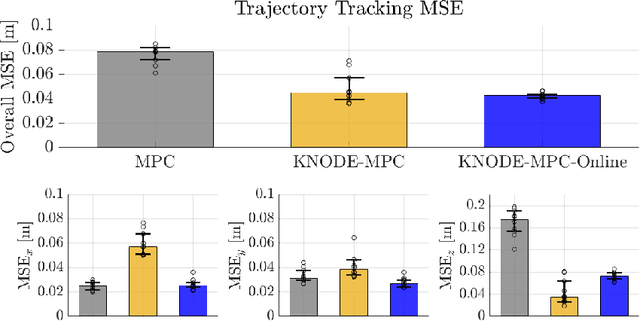
In this work, we consider the task of improving the accuracy of dynamic models for model predictive control (MPC) in an online setting. Even though prediction models can be learned and applied to model-based controllers, these models are often learned offline. In this offline setting, training data is first collected and a prediction model is learned through an elaborated training procedure. After the model is trained to a desired accuracy, it is then deployed in a model predictive controller. However, since the model is learned offline, it does not adapt to disturbances or model errors observed during deployment. To improve the adaptiveness of the model and the controller, we propose an online dynamics learning framework that continually improves the accuracy of the dynamic model during deployment. We adopt knowledge-based neural ordinary differential equations (KNODE) as the dynamic models, and use techniques inspired by transfer learning to continually improve the model accuracy. We demonstrate the efficacy of our framework with a quadrotor robot, and verify the framework in both simulations and physical experiments. Results show that the proposed approach is able to account for disturbances that are possibly time-varying, while maintaining good trajectory tracking performance.

KNODE-MPC: A Knowledge-based Data-driven Predictive Control Framework for Aerial Robots

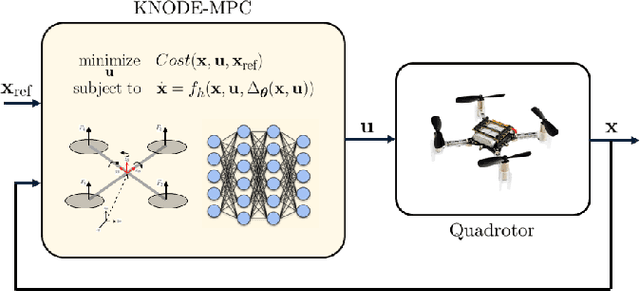
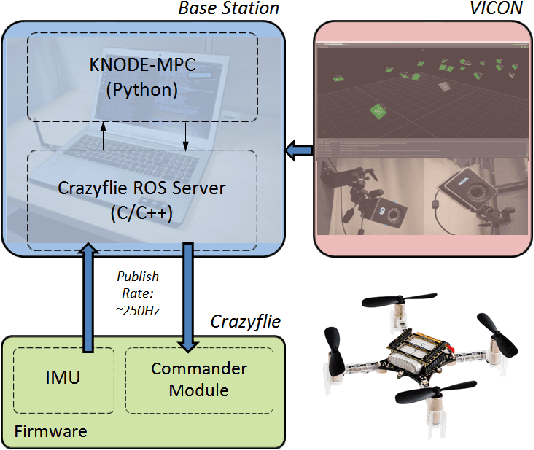
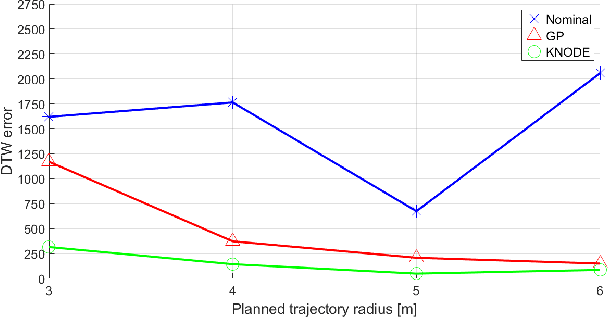
In this work, we consider the problem of deriving and incorporating accurate dynamic models for model predictive control (MPC) with an application to quadrotor control. MPC relies on precise dynamic models to achieve the desired closed-loop performance. However, the presence of uncertainties in complex systems and the environments they operate in poses a challenge in obtaining sufficiently accurate representations of the system dynamics. In this work, we make use of a deep learning tool, knowledge-based neural ordinary differential equations (KNODE), to augment a model obtained from first principles. The resulting hybrid model encompasses both a nominal first-principle model and a neural network learnt from simulated or real-world experimental data. Using a quadrotor, we benchmark our hybrid model against a state-of-the-art Gaussian Process (GP) model and show that the hybrid model provides more accurate predictions of the quadrotor dynamics and is able to generalize beyond the training data. To improve closed-loop performance, the hybrid model is integrated into a novel MPC framework, known as KNODE-MPC. Results show that the integrated framework achieves 73% improvement in simulations and more than 14% in physical experiments, in terms of trajectory tracking performance.