Domain Adaptive Safety Filters via Deep Operator Learning

Learning-based approaches for constructing Control Barrier Functions (CBFs) are increasingly being explored for safety-critical control systems. However, these methods typically require complete retraining when applied to unseen environments, limiting their adaptability. To address this, we propose a self-supervised deep operator learning framework that learns the mapping from environmental parameters to the corresponding CBF, rather than learning the CBF directly. Our approach leverages the residual of a parametric Partial Differential Equation (PDE), where the solution defines a parametric CBF approximating the maximal control invariant set. This framework accommodates complex safety constraints, higher relative degrees, and actuation limits. We demonstrate the effectiveness of the method through numerical experiments on navigation tasks involving dynamic obstacles.

Verification-Aided Learning of Neural Network Barrier Functions with Termination Guarantees

Barrier functions are a general framework for establishing a safety guarantee for a system. However, there is no general method for finding these functions. To address this shortcoming, recent approaches use self-supervised learning techniques to learn these functions using training data that are periodically generated by a verification procedure, leading to a verification-aided learning framework. Despite its immense potential in automating barrier function synthesis, the verification-aided learning framework does not have termination guarantees and may suffer from a low success rate of finding a valid barrier function in practice. In this paper, we propose a holistic approach to address these drawbacks. With a convex formulation of the barrier function synthesis, we propose to first learn an empirically well-behaved NN basis function and then apply a fine-tuning algorithm that exploits the convexity and counterexamples from the verification failure to find a valid barrier function with finite-step termination guarantees: if there exist valid barrier functions, the fine-tuning algorithm is guaranteed to find one in a finite number of iterations. We demonstrate that our fine-tuning method can significantly boost the performance of the verification-aided learning framework on examples of different scales and using various neural network verifiers.

Learning Performance-Oriented Control Barrier Functions Under Complex Safety Constraints and Limited Actuation

Control Barrier Functions (CBFs) provide an elegant framework for designing safety filters for nonlinear control systems by constraining their trajectories to an invariant subset of a prespecified safe set. However, the task of finding a CBF that concurrently maximizes the volume of the resulting control invariant set while accommodating complex safety constraints, particularly in high relative degree systems with actuation constraints, continues to pose a substantial challenge. In this work, we propose a novel self-supervised learning framework that holistically addresses these hurdles. Given a Boolean composition of multiple state constraints that define the safe set, our approach starts with building a single continuously differentiable function whose 0-superlevel set provides an inner approximation of the safe set. We then use this function together with a smooth neural network to parameterize the CBF candidate. Finally, we design a training loss function based on a Hamilton-Jacobi partial differential equation to train the CBF while enlarging the volume of the induced control invariant set. We demonstrate the effectiveness of our approach via numerical experiments.

Lagrangian Properties and Control of Soft Robots Modeled with Discrete Cosserat Rods

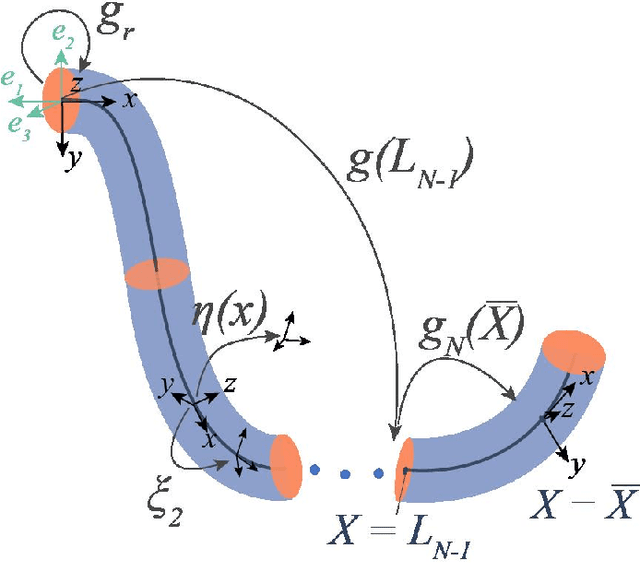
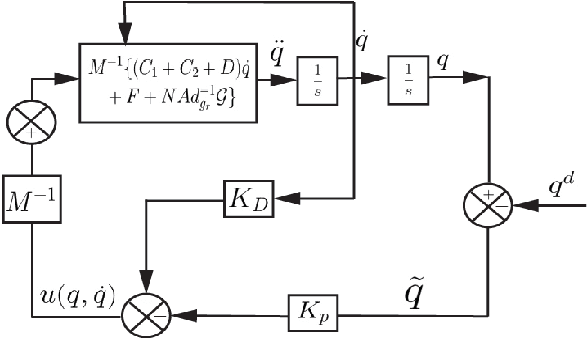
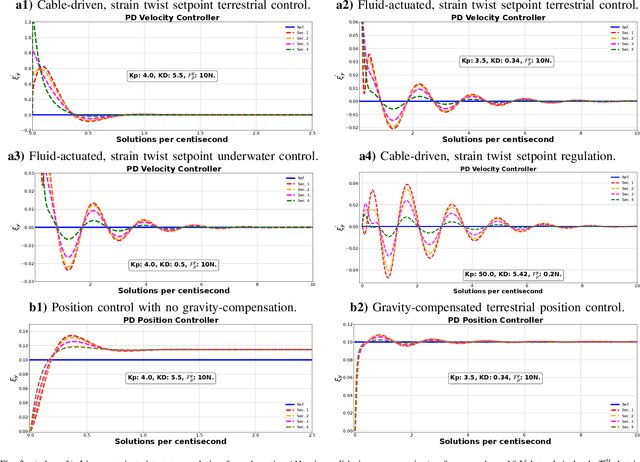
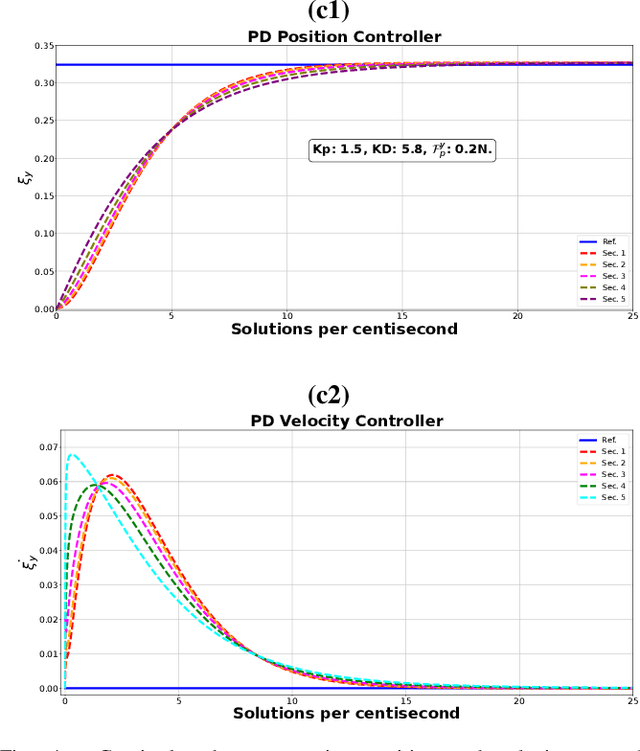
The characteristic ``in-plane" bending associated with soft robots' deformation make them preferred over rigid robots in sophisticated manipulation and movement tasks. Executing such motion strategies to precision in soft deformable robots and structures is however fraught with modeling and control challenges given their infinite degrees-of-freedom. Imposing \textit{piecewise constant strains} (PCS) across (discretized) Cosserat microsolids on the continuum material however, their dynamics become amenable to tractable mathematical analysis. While this PCS model handles the characteristic difficult-to-model ``in-plane" bending well, its Lagrangian properties are not exploited for control in literature neither is there a rigorous study on the dynamic performance of multisection deformable materials for ``in-plane" bending that guarantees steady-state convergence. In this sentiment, we first establish the PCS model's structural Lagrangian properties. Second, we exploit these for control on various strain goal states. Third, we benchmark our hypotheses against an Octopus-inspired robot arm under different constant tip loads. These induce non-constant ``in-plane" deformation and we regulate strain states throughout the continuum in these configurations. Our numerical results establish convergence to desired equilibrium throughout the continuum in all of our tests. Within the bounds here set, we conjecture that our methods can find wide adoption in the control of cable- and fluid-driven multisection soft robotic arms; and may be extensible to the (learning-based) control of deformable agents employed in simulated, mixed, or augmented reality.

PcLast: Discovering Plannable Continuous Latent States

Goal-conditioned planning benefits from learned low-dimensional representations of rich, high-dimensional observations. While compact latent representations, typically learned from variational autoencoders or inverse dynamics, enable goal-conditioned planning they ignore state affordances, thus hampering their sample-efficient planning capabilities. In this paper, we learn a representation that associates reachable states together for effective onward planning. We first learn a latent representation with multi-step inverse dynamics (to remove distracting information); and then transform this representation to associate reachable states together in $\ell_2$ space. Our proposals are rigorously tested in various simulation testbeds. Numerical results in reward-based and reward-free settings show significant improvements in sampling efficiency, and yields layered state abstractions that enable computationally efficient hierarchical planning.

Safety Filter Design for Neural Network Systems via Convex Optimization

With the increase in data availability, it has been widely demonstrated that neural networks (NN) can capture complex system dynamics precisely in a data-driven manner. However, the architectural complexity and nonlinearity of the NNs make it challenging to synthesize a provably safe controller. In this work, we propose a novel safety filter that relies on convex optimization to ensure safety for a NN system, subject to additive disturbances that are capable of capturing modeling errors. Our approach leverages tools from NN verification to over-approximate NN dynamics with a set of linear bounds, followed by an application of robust linear MPC to search for controllers that can guarantee robust constraint satisfaction. We demonstrate the efficacy of the proposed framework numerically on a nonlinear pendulum system.

Differentiable Safe Controller Design through Control Barrier Functions

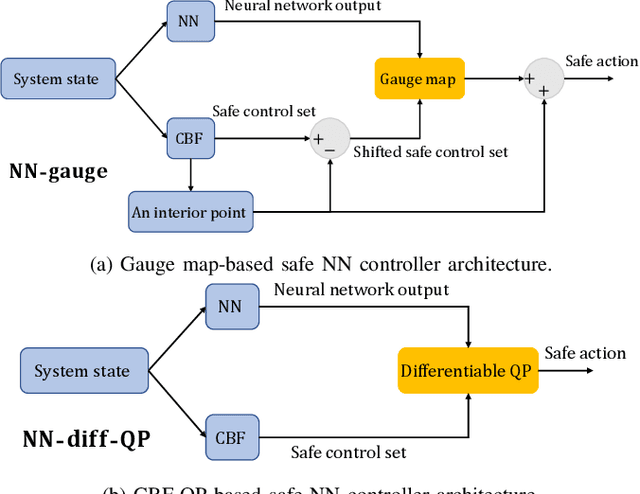
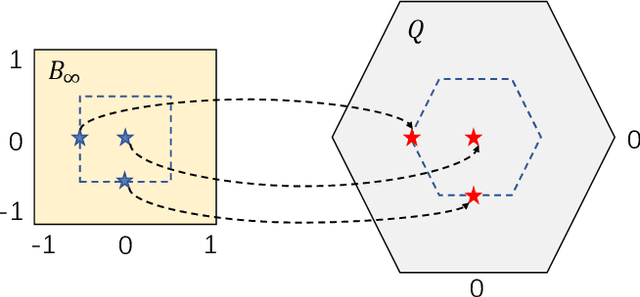
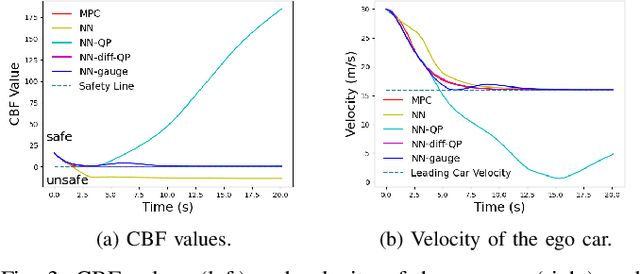
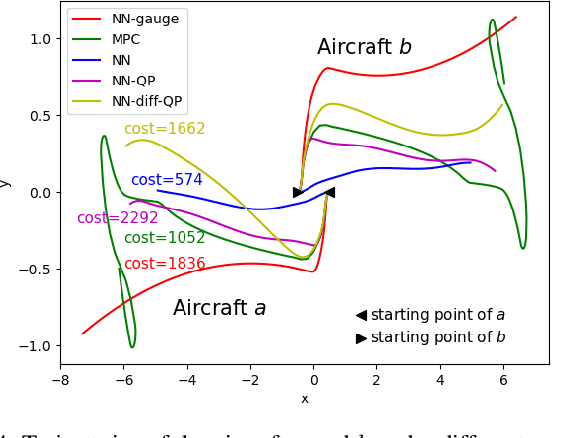
Learning-based controllers, such as neural network (NN) controllers, can show high empirical performance but lack formal safety guarantees. To address this issue, control barrier functions (CBFs) have been applied as a safety filter to monitor and modify the outputs of learning-based controllers in order to guarantee the safety of the closed-loop system. However, such modification can be myopic with unpredictable long-term effects. In this work, we propose a safe-by-construction NN controller which employs differentiable CBF-based safety layers, and investigate the performance of safe-by-construction NN controllers in learning-based control. Specifically, two formulations of controllers are compared: one is projection-based and the other relies on our proposed set-theoretic parameterization. Both methods demonstrate improved closed-loop performance over using CBF as a separate safety filter in numerical experiments.

DeepSplit: Scalable Verification of Deep Neural Networks via Operator Splitting

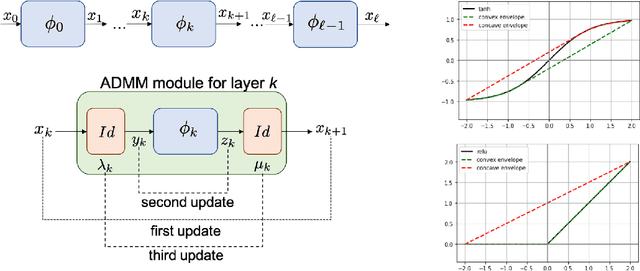
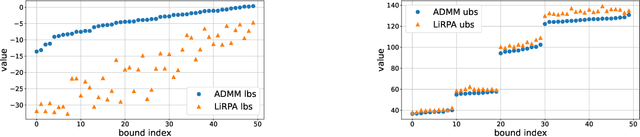
Analyzing the worst-case performance of deep neural networks against input perturbations amounts to solving a large-scale non-convex optimization problem, for which several past works have proposed convex relaxations as a promising alternative. However, even for reasonably-sized neural networks, these relaxations are not tractable, and so must be replaced by even weaker relaxations in practice. In this work, we propose a novel operator splitting method that can directly solve a convex relaxation of the problem to high accuracy, by splitting it into smaller sub-problems that often have analytical solutions. The method is modular and scales to problem instances that were previously impossible to solve exactly due to their size. Furthermore, the solver operations are amenable to fast parallelization with GPU acceleration. We demonstrate our method in obtaining tighter bounds on the worst-case performance of large convolutional networks in image classification and reinforcement learning settings.