Stable and Transferable Hyper-Graph Neural Networks

We introduce an architecture for processing signals supported on hypergraphs via graph neural networks (GNNs), which we call a Hyper-graph Expansion Neural Network (HENN), and provide the first bounds on the stability and transferability error of a hypergraph signal processing model. To do so, we provide a framework for bounding the stability and transferability error of GNNs across arbitrary graphs via spectral similarity. By bounding the difference between two graph shift operators (GSOs) in the positive semi-definite sense via their eigenvalue spectrum, we show that this error depends only on the properties of the GNN and the magnitude of spectral similarity of the GSOs. Moreover, we show that existing transferability results that assume the graphs are small perturbations of one another, or that the graphs are random and drawn from the same distribution or sampled from the same graphon can be recovered using our approach. Thus, both GNNs and our HENNs (trained using normalized Laplacians as graph shift operators) will be increasingly stable and transferable as the graphs become larger. Experimental results illustrate the importance of considering multiple graph representations in HENN, and show its superior performance when transferability is desired.

Differentiable Safe Controller Design through Control Barrier Functions

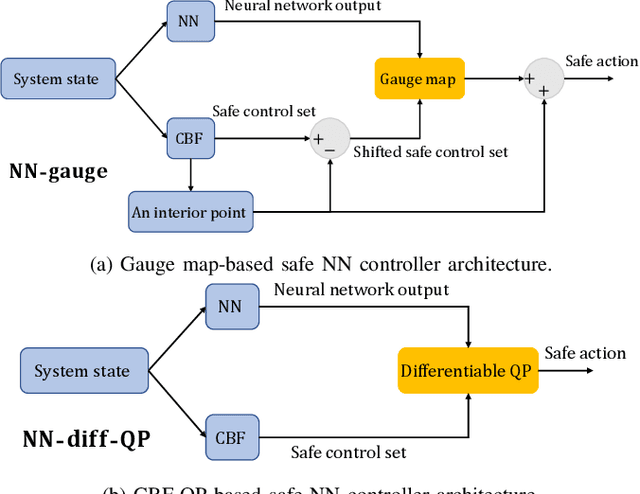
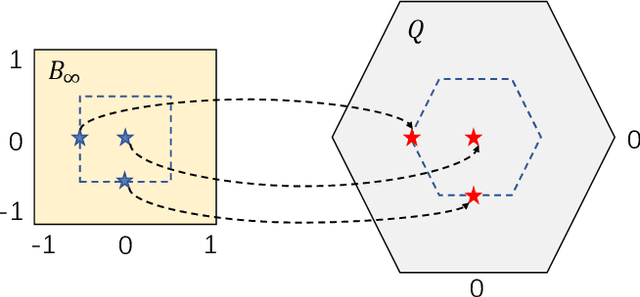
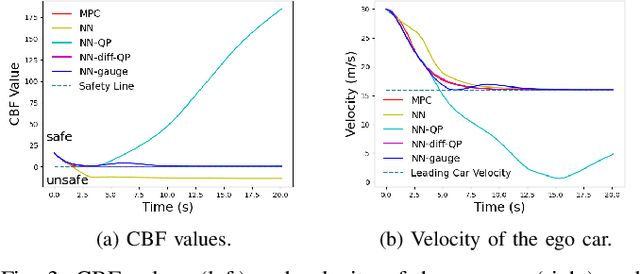
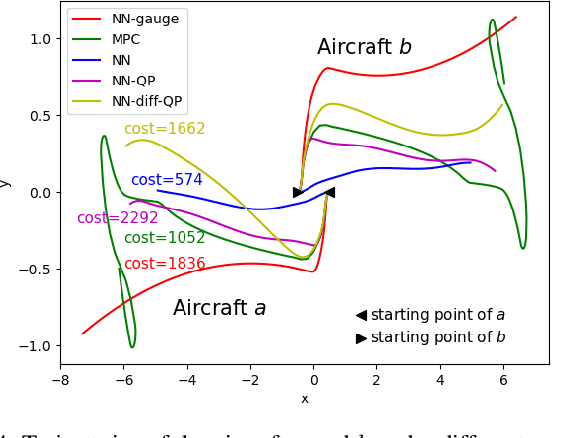
Learning-based controllers, such as neural network (NN) controllers, can show high empirical performance but lack formal safety guarantees. To address this issue, control barrier functions (CBFs) have been applied as a safety filter to monitor and modify the outputs of learning-based controllers in order to guarantee the safety of the closed-loop system. However, such modification can be myopic with unpredictable long-term effects. In this work, we propose a safe-by-construction NN controller which employs differentiable CBF-based safety layers, and investigate the performance of safe-by-construction NN controllers in learning-based control. Specifically, two formulations of controllers are compared: one is projection-based and the other relies on our proposed set-theoretic parameterization. Both methods demonstrate improved closed-loop performance over using CBF as a separate safety filter in numerical experiments.

Learning Operators with Coupled Attention

Supervised operator learning is an emerging machine learning paradigm with applications to modeling the evolution of spatio-temporal dynamical systems and approximating general black-box relationships between functional data. We propose a novel operator learning method, LOCA (Learning Operators with Coupled Attention), motivated from the recent success of the attention mechanism. In our architecture, the input functions are mapped to a finite set of features which are then averaged with attention weights that depend on the output query locations. By coupling these attention weights together with an integral transform, LOCA is able to explicitly learn correlations in the target output functions, enabling us to approximate nonlinear operators even when the number of output function in the training set measurements is very small. Our formulation is accompanied by rigorous approximation theoretic guarantees on the universal expressiveness of the proposed model. Empirically, we evaluate the performance of LOCA on several operator learning scenarios involving systems governed by ordinary and partial differential equations, as well as a black-box climate prediction problem. Through these scenarios we demonstrate state of the art accuracy, robustness with respect to noisy input data, and a consistently small spread of errors over testing data sets, even for out-of-distribution prediction tasks.

Stabilization of Complementarity Systems via Contact-Aware Controllers

We propose a framework for provably stable local control of multi-contact robotic systems, directly utilizing force measurements and exploiting the complementarity structure of contact dynamics. Since many robotic tasks, like manipulation and locomotion, are fundamentally based in making and breaking contact with the environment, state-of-the-art control policies struggle to deal with the hybrid nature of multi-contact motion. Such controllers often rely heavily upon heuristics or, due to the combinatoric structure in the dynamics, are unsuitable for real-time control. Principled deployment of tactile sensors offers a promising mechanism for stable and robust control, but modern approaches often use this data in an ad hoc manner, for instance to guide guarded moves. In this work, we present a control framework which can close the loop on tactile sensors. Critically, this framework is non-combinatoric, enabling optimization algorithms to automatically synthesize provably stable control policies. We demonstrate this approach on multiple examples, including underactuated multi-contact problems, quasi-static friction problems and a high-dimensional problem with ten contacts.

Robust Deep Learning as Optimal Control: Insights and Convergence Guarantees

The fragility of deep neural networks to adversarially-chosen inputs has motivated the need to revisit deep learning algorithms. Including adversarial examples during training is a popular defense mechanism against adversarial attacks. This mechanism can be formulated as a min-max optimization problem, where the adversary seeks to maximize the loss function using an iterative first-order algorithm while the learner attempts to minimize it. However, finding adversarial examples in this way causes excessive computational overhead during training. By interpreting the min-max problem as an optimal control problem, it has recently been shown that one can exploit the compositional structure of neural networks in the optimization problem to improve the training time significantly. In this paper, we provide the first convergence analysis of this adversarial training algorithm by combining techniques from robust optimal control and inexact oracle methods in optimization. Our analysis sheds light on how the hyperparameters of the algorithm affect the its stability and convergence. We support our insights with experiments on a robust classification problem.

Contact-Aware Controller Design for Complementarity Systems

While many robotic tasks, like manipulation and locomotion, are fundamentally based in making and breaking contact with the environment, state-of-the-art control policies struggle to deal with the hybrid nature of multi-contact motion. Such controllers often rely heavily upon heuristics or, due to the combinatoric structure in the dynamics, are unsuitable for real-time control. Principled deployment of tactile sensors offers a promising mechanism for stable and robust control, but modern approaches often use this data in an ad hoc manner, for instance to guide guarded moves. In this work, by exploiting the complementarity structure of contact dynamics, we propose a control framework which can close the loop on rich, tactile sensors. Critically, this framework is non-combinatoric, enabling optimization algorithms to automatically synthesize provably stable control policies. We demonstrate this approach on three different underactuated, multi-contact robotics problems.

Joint Estimation and Localization in Sensor Networks

This paper addresses the problem of collaborative tracking of dynamic targets in wireless sensor networks. A novel distributed linear estimator, which is a version of a distributed Kalman filter, is derived. We prove that the filter is mean square consistent in the case of static target estimation. When large sensor networks are deployed, it is common that the sensors do not have good knowledge of their locations, which affects the target estimation procedure. Unlike most existing approaches for target tracking, we investigate the performance of our filter when the sensor poses need to be estimated by an auxiliary localization procedure. The sensors are localized via a distributed Jacobi algorithm from noisy relative measurements. We prove strong convergence guarantees for the localization method and in turn for the joint localization and target estimation approach. The performance of our algorithms is demonstrated in simulation on environmental monitoring and target tracking tasks.