Distributionally Robust Clustered Federated Learning: A Case Study in Healthcare

In this paper, we address the challenge of heterogeneous data distributions in cross-silo federated learning by introducing a novel algorithm, which we term Cross-silo Robust Clustered Federated Learning (CS-RCFL). Our approach leverages the Wasserstein distance to construct ambiguity sets around each client's empirical distribution that capture possible distribution shifts in the local data, enabling evaluation of worst-case model performance. We then propose a model-agnostic integer fractional program to determine the optimal distributionally robust clustering of clients into coalitions so that possible biases in the local models caused by statistically heterogeneous client datasets are avoided, and analyze our method for linear and logistic regression models. Finally, we discuss a federated learning protocol that ensures the privacy of client distributions, a critical consideration, for instance, when clients are healthcare institutions. We evaluate our algorithm on synthetic and real-world healthcare data.

Path Signatures and Graph Neural Networks for Slow Earthquake Analysis: Better Together?

The path signature, having enjoyed recent success in the machine learning community, is a theoretically-driven method for engineering features from irregular paths. On the other hand, graph neural networks (GNN), neural architectures for processing data on graphs, excel on tasks with irregular domains, such as sensor networks. In this paper, we introduce a novel approach, Path Signature Graph Convolutional Neural Networks (PS-GCNN), integrating path signatures into graph convolutional neural networks (GCNN), and leveraging the strengths of both path signatures, for feature extraction, and GCNNs, for handling spatial interactions. We apply our method to analyze slow earthquake sequences, also called slow slip events (SSE), utilizing data from GPS timeseries, with a case study on a GPS sensor network on the east coast of New Zealand's north island. We also establish benchmarks for our method on simulated stochastic differential equations, which model similar reaction-diffusion phenomenon. Our methodology shows promise for future advancement in earthquake prediction and sensor network analysis.

Lattice Theory in Multi-Agent Systems

In this thesis, we argue that (order-) lattice-based multi-agent information systems constitute a broad class of networked multi-agent systems in which relational data is passed between nodes. Mathematically modeled as lattice-valued sheaves, we initiate a discrete Hodge theory with a Laplace operator, analogous to the graph Laplacian and the graph connection Laplacian, acting on assignments of data to the nodes of a Tarski sheaf. The Hodge-Tarski theorem (the main theorem) relates the fixed point theory of this operator, called the Tarski Laplacian in deference to the Tarski Fixed Point Theorem, to the global sections (consistent global states) of the sheaf. We present novel applications to signal processing and multi-agent semantics and supply a plethora of examples throughout.

Tangent Bundle Convolutional Learning: from Manifolds to Cellular Sheaves and Back

In this work we introduce a convolution operation over the tangent bundle of Riemann manifolds in terms of exponentials of the Connection Laplacian operator. We define tangent bundle filters and tangent bundle neural networks (TNNs) based on this convolution operation, which are novel continuous architectures operating on tangent bundle signals, i.e. vector fields over the manifolds. Tangent bundle filters admit a spectral representation that generalizes the ones of scalar manifold filters, graph filters and standard convolutional filters in continuous time. We then introduce a discretization procedure, both in the space and time domains, to make TNNs implementable, showing that their discrete counterpart is a novel principled variant of the very recently introduced sheaf neural networks. We formally prove that this discretized architecture converges to the underlying continuous TNN. Finally, we numerically evaluate the effectiveness of the proposed architecture on various learning tasks, both on synthetic and real data.

Tangent Bundle Filters and Neural Networks: from Manifolds to Cellular Sheaves and Back

In this work we introduce a convolution operation over the tangent bundle of Riemannian manifolds exploiting the Connection Laplacian operator. We use the convolution to define tangent bundle filters and tangent bundle neural networks (TNNs), novel continuous architectures operating on tangent bundle signals, i.e. vector fields over manifolds. We discretize TNNs both in space and time domains, showing that their discrete counterpart is a principled variant of the recently introduced Sheaf Neural Networks. We formally prove that this discrete architecture converges to the underlying continuous TNN. We numerically evaluate the effectiveness of the proposed architecture on a denoising task of a tangent vector field over the unit 2-sphere.

Stable and Transferable Hyper-Graph Neural Networks

We introduce an architecture for processing signals supported on hypergraphs via graph neural networks (GNNs), which we call a Hyper-graph Expansion Neural Network (HENN), and provide the first bounds on the stability and transferability error of a hypergraph signal processing model. To do so, we provide a framework for bounding the stability and transferability error of GNNs across arbitrary graphs via spectral similarity. By bounding the difference between two graph shift operators (GSOs) in the positive semi-definite sense via their eigenvalue spectrum, we show that this error depends only on the properties of the GNN and the magnitude of spectral similarity of the GSOs. Moreover, we show that existing transferability results that assume the graphs are small perturbations of one another, or that the graphs are random and drawn from the same distribution or sampled from the same graphon can be recovered using our approach. Thus, both GNNs and our HENNs (trained using normalized Laplacians as graph shift operators) will be increasingly stable and transferable as the graphs become larger. Experimental results illustrate the importance of considering multiple graph representations in HENN, and show its superior performance when transferability is desired.

Multidimensional Persistence Module Classification via Lattice-Theoretic Convolutions

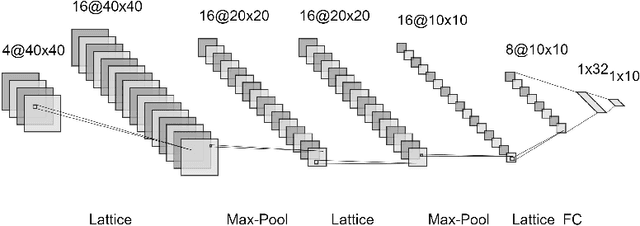
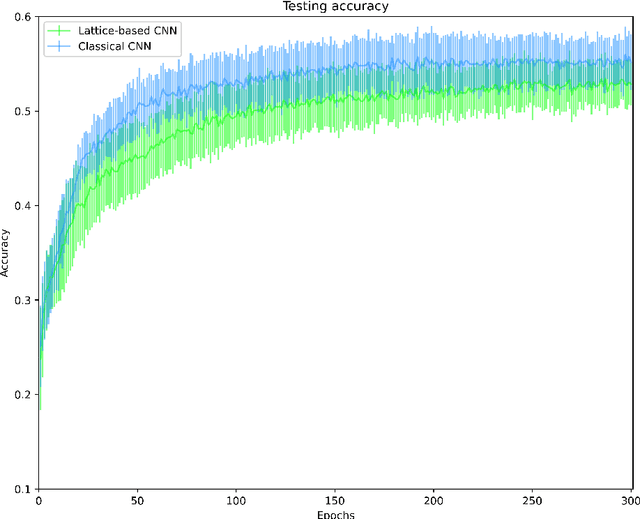
Multiparameter persistent homology has been largely neglected as an input to machine learning algorithms. We consider the use of lattice-based convolutional neural network layers as a tool for the analysis of features arising from multiparameter persistence modules. We find that these show promise as an alternative to convolutions for the classification of multidimensional persistence modules.

Quiver Signal Processing (QSP)

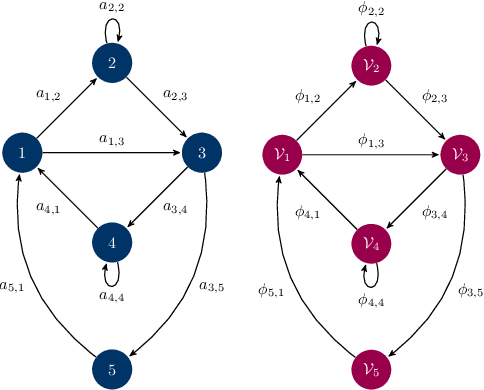
In this paper we state the basics for a signal processing framework on quiver representations. A quiver is a directed graph and a quiver representation is an assignment of vector spaces to the nodes of the graph and of linear maps between the vector spaces associated to the nodes. Leveraging the tools from representation theory, we propose a signal processing framework that allows us to handle heterogeneous multidimensional information in networks. We provide a set of examples where this framework provides a natural set of tools to understand apparently hidden structure in information. We remark that the proposed framework states the basis for building graph neural networks where information can be processed and handled in alternative ways.