Using Domain Knowledge with Deep Learning to Solve Applied Inverse Problems

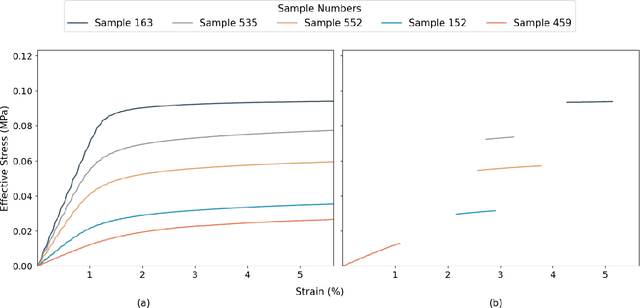
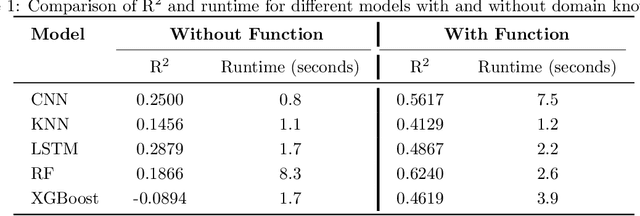
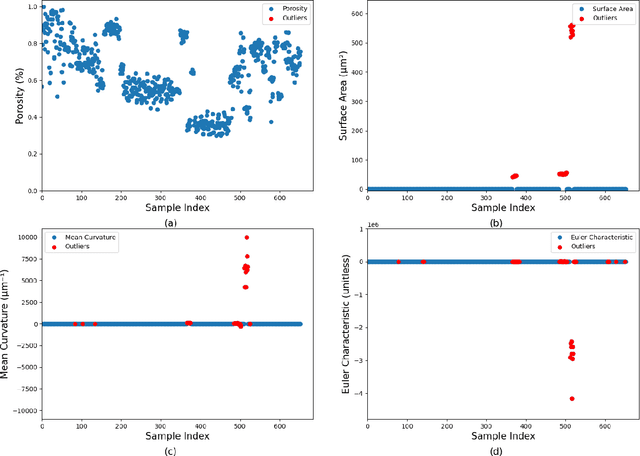
Advancements in deep learning have improved the ability to model complex, nonlinear relationships, such as those encountered in complex material inverse problems. However, the effectiveness of these methods often depends on large datasets, which are not always available. In this study, the incorporation of domain-specific knowledge of mechanical behavior is investigated to evaluate the impact on the predictive performance of the models in data-scarce scenarios. To demonstrate this, stress-strain curves were used to predict key microstructural features of porous materials, and the performance of models trained with and without domain knowledge was compared using five deep learning models: Convolutional Neural Networks, Extreme Gradient Boosting, K-Nearest Neighbors, Long Short-Term Memory, and Random Forest. The results of the models with domain-specific characteristics consistently achieved higher $R^2$ values and improved learning efficiency compared to models without prior knowledge. When the models did not include domain knowledge, the model results revealed meaningful patterns were not recognized, while those enhanced with mechanical insights showed superior feature extraction and predictions. These findings underscore the critical role of domain knowledge in guiding deep learning models, highlighting the need to combine domain expertise with data-driven approaches to achieve reliable and accurate outcomes in materials science and related fields.

Path Signatures and Graph Neural Networks for Slow Earthquake Analysis: Better Together?

The path signature, having enjoyed recent success in the machine learning community, is a theoretically-driven method for engineering features from irregular paths. On the other hand, graph neural networks (GNN), neural architectures for processing data on graphs, excel on tasks with irregular domains, such as sensor networks. In this paper, we introduce a novel approach, Path Signature Graph Convolutional Neural Networks (PS-GCNN), integrating path signatures into graph convolutional neural networks (GCNN), and leveraging the strengths of both path signatures, for feature extraction, and GCNNs, for handling spatial interactions. We apply our method to analyze slow earthquake sequences, also called slow slip events (SSE), utilizing data from GPS timeseries, with a case study on a GPS sensor network on the east coast of New Zealand's north island. We also establish benchmarks for our method on simulated stochastic differential equations, which model similar reaction-diffusion phenomenon. Our methodology shows promise for future advancement in earthquake prediction and sensor network analysis.