Graph Semi-Supervised Learning for Point Classification on Data Manifolds

We propose a graph semi-supervised learning framework for classification tasks on data manifolds. Motivated by the manifold hypothesis, we model data as points sampled from a low-dimensional manifold $\mathcal{M} \subset \mathbb{R}^F$. The manifold is approximated in an unsupervised manner using a variational autoencoder (VAE), where the trained encoder maps data to embeddings that represent their coordinates in $\mathbb{R}^F$. A geometric graph is constructed with Gaussian-weighted edges inversely proportional to distances in the embedding space, transforming the point classification problem into a semi-supervised node classification task on the graph. This task is solved using a graph neural network (GNN). Our main contribution is a theoretical analysis of the statistical generalization properties of this data-to-manifold-to-graph pipeline. We show that, under uniform sampling from $\mathcal{M}$, the generalization gap of the semi-supervised task diminishes with increasing graph size, up to the GNN training error. Leveraging a training procedure which resamples a slightly larger graph at regular intervals during training, we then show that the generalization gap can be reduced even further, vanishing asymptotically. Finally, we validate our findings with numerical experiments on image classification benchmarks, demonstrating the empirical effectiveness of our approach.

Wireless Link Scheduling with State-Augmented Graph Neural Networks

We consider the problem of optimal link scheduling in large-scale wireless ad hoc networks. We specifically aim for the maximum long-term average performance, subject to a minimum transmission requirement for each link to ensure fairness. With a graph structure utilized to represent the conflicts of links, we formulate a constrained optimization problem to learn the scheduling policy, which is parameterized with a graph neural network (GNN). To address the challenge of long-term performance, we use the state-augmentation technique. In particular, by augmenting the Lagrangian dual variables as dynamic inputs to the scheduling policy, the GNN can be trained to gradually adapt the scheduling decisions to achieve the minimum transmission requirements. We verify the efficacy of our proposed policy through numerical simulations and compare its performance with several baselines in various network settings.

Generalization of Geometric Graph Neural Networks

In this paper, we study the generalization capabilities of geometric graph neural networks (GNNs). We consider GNNs over a geometric graph constructed from a finite set of randomly sampled points over an embedded manifold with topological information captured. We prove a generalization gap between the optimal empirical risk and the optimal statistical risk of this GNN, which decreases with the number of sampled points from the manifold and increases with the dimension of the underlying manifold. This generalization gap ensures that the GNN trained on a graph on a set of sampled points can be utilized to process other unseen graphs constructed from the same underlying manifold. The most important observation is that the generalization capability can be realized with one large graph instead of being limited to the size of the graph as in previous results. The generalization gap is derived based on the non-asymptotic convergence result of a GNN on the sampled graph to the underlying manifold neural networks (MNNs). We verify this theoretical result with experiments on both Arxiv dataset and Cora dataset.

Generalization of Graph Neural Networks is Robust to Model Mismatch

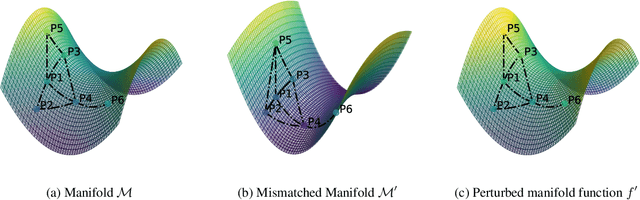
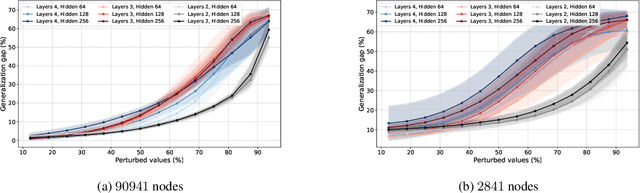
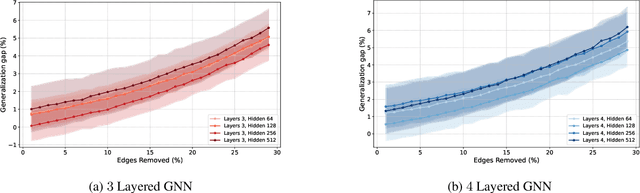
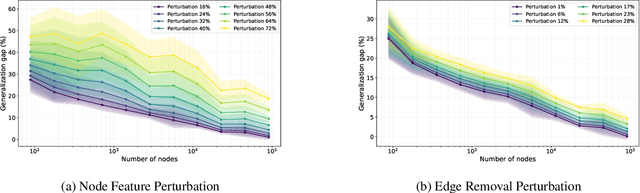
Graph neural networks (GNNs) have demonstrated their effectiveness in various tasks supported by their generalization capabilities. However, the current analysis of GNN generalization relies on the assumption that training and testing data are independent and identically distributed (i.i.d). This imposes limitations on the cases where a model mismatch exists when generating testing data. In this paper, we examine GNNs that operate on geometric graphs generated from manifold models, explicitly focusing on scenarios where there is a mismatch between manifold models generating training and testing data. Our analysis reveals the robustness of the GNN generalization in the presence of such model mismatch. This indicates that GNNs trained on graphs generated from a manifold can still generalize well to unseen nodes and graphs generated from a mismatched manifold. We attribute this mismatch to both node feature perturbations and edge perturbations within the generated graph. Our findings indicate that the generalization gap decreases as the number of nodes grows in the training graph while increasing with larger manifold dimension as well as larger mismatch. Importantly, we observe a trade-off between the generalization of GNNs and the capability to discriminate high-frequency components when facing a model mismatch. The most important practical consequence of this analysis is to shed light on the filter design of generalizable GNNs robust to model mismatch. We verify our theoretical findings with experiments on multiple real-world datasets.

A Manifold Perspective on the Statistical Generalization of Graph Neural Networks

Convolutional neural networks have been successfully extended to operate on graphs, giving rise to Graph Neural Networks (GNNs). GNNs combine information from adjacent nodes by successive applications of graph convolutions. GNNs have been implemented successfully in various learning tasks while the theoretical understanding of their generalization capability is still in progress. In this paper, we leverage manifold theory to analyze the statistical generalization gap of GNNs operating on graphs constructed on sampled points from manifolds. We study the generalization gaps of GNNs on both node-level and graph-level tasks. We show that the generalization gaps decrease with the number of nodes in the training graphs, which guarantees the generalization of GNNs to unseen points over manifolds. We validate our theoretical results in multiple real-world datasets.

Geometric Graph Filters and Neural Networks: Limit Properties and Discriminability Trade-offs

This paper studies the relationship between a graph neural network (GNN) and a manifold neural network (MNN) when the graph is constructed from a set of points sampled from the manifold, thus encoding geometric information. We consider convolutional MNNs and GNNs where the manifold and the graph convolutions are respectively defined in terms of the Laplace-Beltrami operator and the graph Laplacian. Using the appropriate kernels, we analyze both dense and moderately sparse graphs. We prove non-asymptotic error bounds showing that convolutional filters and neural networks on these graphs converge to convolutional filters and neural networks on the continuous manifold. As a byproduct of this analysis, we observe an important trade-off between the discriminability of graph filters and their ability to approximate the desired behavior of manifold filters. We then discuss how this trade-off is ameliorated in neural networks due to the frequency mixing property of nonlinearities. We further derive a transferability corollary for geometric graphs sampled from the same manifold. We validate our results numerically on a navigation control problem and a point cloud classification task.

Tangent Bundle Convolutional Learning: from Manifolds to Cellular Sheaves and Back

In this work we introduce a convolution operation over the tangent bundle of Riemann manifolds in terms of exponentials of the Connection Laplacian operator. We define tangent bundle filters and tangent bundle neural networks (TNNs) based on this convolution operation, which are novel continuous architectures operating on tangent bundle signals, i.e. vector fields over the manifolds. Tangent bundle filters admit a spectral representation that generalizes the ones of scalar manifold filters, graph filters and standard convolutional filters in continuous time. We then introduce a discretization procedure, both in the space and time domains, to make TNNs implementable, showing that their discrete counterpart is a novel principled variant of the very recently introduced sheaf neural networks. We formally prove that this discretized architecture converges to the underlying continuous TNN. Finally, we numerically evaluate the effectiveness of the proposed architecture on various learning tasks, both on synthetic and real data.

Graphon Pooling for Reducing Dimensionality of Signals and Convolutional Operators on Graphs

In this paper we propose a pooling approach for convolutional information processing on graphs relying on the theory of graphons and limits of dense graph sequences. We present three methods that exploit the induced graphon representation of graphs and graph signals on partitions of [0, 1]2 in the graphon space. As a result we derive low dimensional representations of the convolutional operators, while a dimensionality reduction of the signals is achieved by simple local interpolation of functions in L2([0, 1]). We prove that those low dimensional representations constitute a convergent sequence of graphs and graph signals, respectively. The methods proposed and the theoretical guarantees that we provide show that the reduced graphs and signals inherit spectral-structural properties of the original quantities. We evaluate our approach with a set of numerical experiments performed on graph neural networks (GNNs) that rely on graphon pooling. We observe that graphon pooling performs significantly better than other approaches proposed in the literature when dimensionality reduction ratios between layers are large. We also observe that when graphon pooling is used we have, in general, less overfitting and lower computational cost.

Convolutional Filtering on Sampled Manifolds

The increasing availability of geometric data has motivated the need for information processing over non-Euclidean domains modeled as manifolds. The building block for information processing architectures with desirable theoretical properties such as invariance and stability is convolutional filtering. Manifold convolutional filters are defined from the manifold diffusion sequence, constructed by successive applications of the Laplace-Beltrami operator to manifold signals. However, the continuous manifold model can only be accessed by sampling discrete points and building an approximate graph model from the sampled manifold. Effective linear information processing on the manifold requires quantifying the error incurred when approximating manifold convolutions with graph convolutions. In this paper, we derive a non-asymptotic error bound for this approximation, showing that convolutional filtering on the sampled manifold converges to continuous manifold filtering. Our findings are further demonstrated empirically on a problem of navigation control.

Tangent Bundle Filters and Neural Networks: from Manifolds to Cellular Sheaves and Back

In this work we introduce a convolution operation over the tangent bundle of Riemannian manifolds exploiting the Connection Laplacian operator. We use the convolution to define tangent bundle filters and tangent bundle neural networks (TNNs), novel continuous architectures operating on tangent bundle signals, i.e. vector fields over manifolds. We discretize TNNs both in space and time domains, showing that their discrete counterpart is a principled variant of the recently introduced Sheaf Neural Networks. We formally prove that this discrete architecture converges to the underlying continuous TNN. We numerically evaluate the effectiveness of the proposed architecture on a denoising task of a tangent vector field over the unit 2-sphere.