Generalization of Graph Neural Networks is Robust to Model Mismatch
Paper and Code
Aug 25, 2024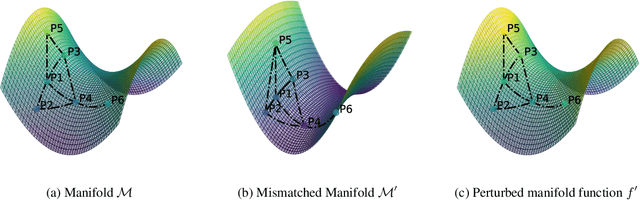
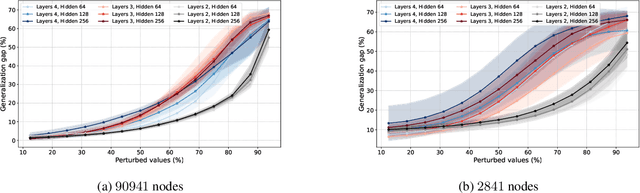
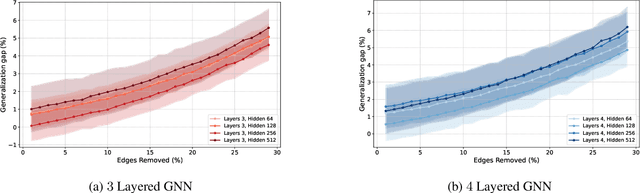
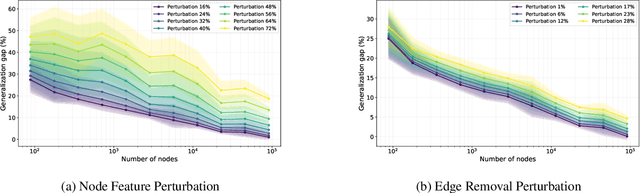
Graph neural networks (GNNs) have demonstrated their effectiveness in various tasks supported by their generalization capabilities. However, the current analysis of GNN generalization relies on the assumption that training and testing data are independent and identically distributed (i.i.d). This imposes limitations on the cases where a model mismatch exists when generating testing data. In this paper, we examine GNNs that operate on geometric graphs generated from manifold models, explicitly focusing on scenarios where there is a mismatch between manifold models generating training and testing data. Our analysis reveals the robustness of the GNN generalization in the presence of such model mismatch. This indicates that GNNs trained on graphs generated from a manifold can still generalize well to unseen nodes and graphs generated from a mismatched manifold. We attribute this mismatch to both node feature perturbations and edge perturbations within the generated graph. Our findings indicate that the generalization gap decreases as the number of nodes grows in the training graph while increasing with larger manifold dimension as well as larger mismatch. Importantly, we observe a trade-off between the generalization of GNNs and the capability to discriminate high-frequency components when facing a model mismatch. The most important practical consequence of this analysis is to shed light on the filter design of generalizable GNNs robust to model mismatch. We verify our theoretical findings with experiments on multiple real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge