Knowledge Sheaves: A Sheaf-Theoretic Framework for Knowledge Graph Embedding

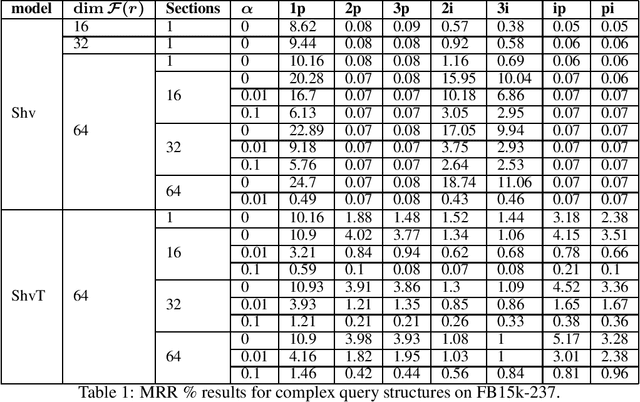
Knowledge graph embedding involves learning representations of entities -- the vertices of the graph -- and relations -- the edges of the graph -- such that the resulting representations encode the known factual information represented by the knowledge graph are internally consistent and can be used in the inference of new relations. We show that knowledge graph embedding is naturally expressed in the topological and categorical language of \textit{cellular sheaves}: learning a knowledge graph embedding corresponds to learning a \textit{knowledge sheaf} over the graph, subject to certain constraints. In addition to providing a generalized framework for reasoning about knowledge graph embedding models, this sheaf-theoretic perspective admits the expression of a broad class of prior constraints on embeddings and offers novel inferential capabilities. We leverage the recently developed spectral theory of sheaf Laplacians to understand the local and global consistency of embeddings and develop new methods for reasoning over composite relations through harmonic extension with respect to the sheaf Laplacian. We then implement these ideas to highlight the benefits of the extensions inspired by this new perspective.

Sheaf Neural Networks

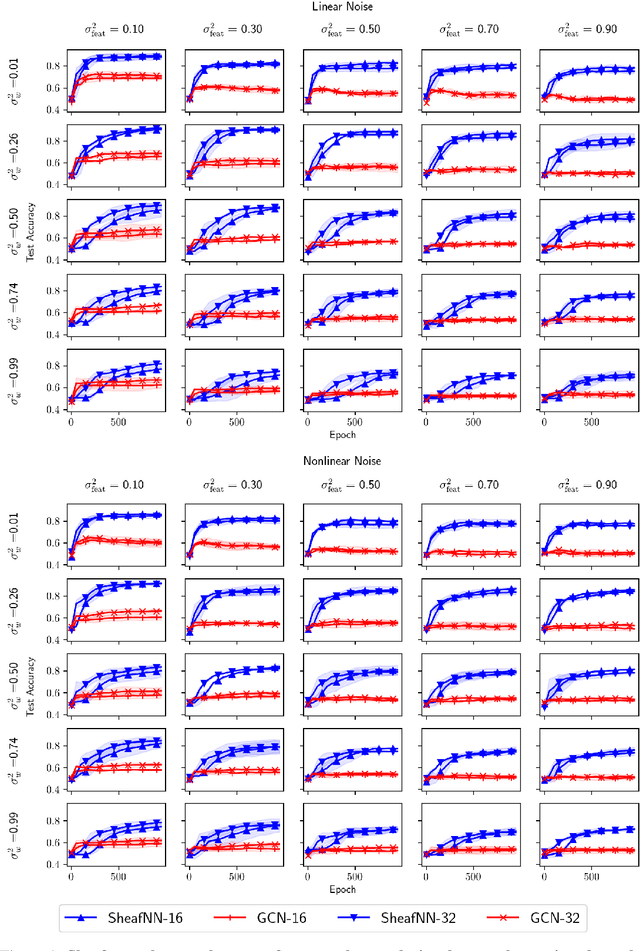
We present a generalization of graph convolutional networks by generalizing the diffusion operation underlying this class of graph neural networks. These sheaf neural networks are based on the sheaf Laplacian, a generalization of the graph Laplacian that encodes additional relational structure parameterized by the underlying graph. The sheaf Laplacian and associated matrices provide an extended version of the diffusion operation in graph convolutional networks, providing a proper generalization for domains where relations between nodes are non-constant, asymmetric, and varying in dimension. We show that the resulting sheaf neural networks can outperform graph convolutional networks in domains where relations between nodes are asymmetric and signed.

Multidimensional Persistence Module Classification via Lattice-Theoretic Convolutions

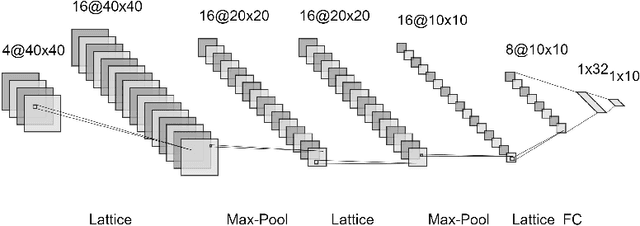
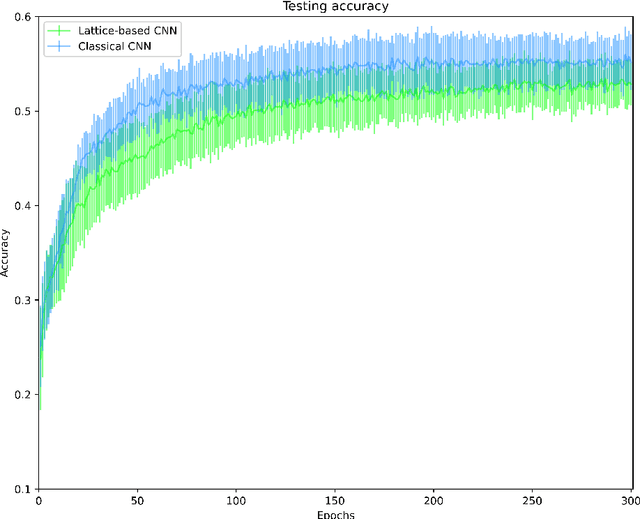
Multiparameter persistent homology has been largely neglected as an input to machine learning algorithms. We consider the use of lattice-based convolutional neural network layers as a tool for the analysis of features arising from multiparameter persistence modules. We find that these show promise as an alternative to convolutions for the classification of multidimensional persistence modules.

Consistency constraints for overlapping data clustering

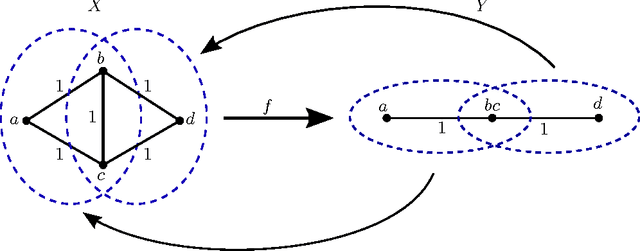
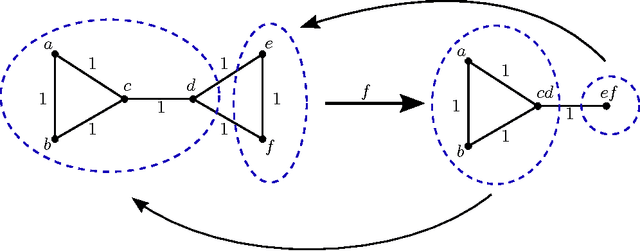
We examine overlapping clustering schemes with functorial constraints, in the spirit of Carlsson--Memoli. This avoids issues arising from the chaining required by partition-based methods. Our principal result shows that any clustering functor is naturally constrained to refine single-linkage clusters and be refined by maximal-linkage clusters. We work in the context of metric spaces with non-expansive maps, which is appropriate for modeling data processing which does not increase information content.