Sensemaking in Novel Environments: How Human Cognition Can Inform Artificial Agents

One of the most vital cognitive skills to possess is the ability to make sense of objects, events, and situations in the world. In the current paper, we offer an approach for creating artificially intelligent agents with the capacity for sensemaking in novel environments. Objectives: to present several key ideas: (1) a novel unified conceptual framework for sensemaking (which includes the existence of sign relations embedded within and across frames); (2) interaction among various content-addressable, distributed-knowledge structures via shared attributes (whose net response would represent a synthesized object, event, or situation serving as a sign for sensemaking in a novel environment). Findings: we suggest that attributes across memories can be shared and recombined in novel ways to create synthesized signs, which can denote certain outcomes in novel environments (i.e., sensemaking).

Stacked Universal Successor Feature Approximators for Safety in Reinforcement Learning

Real-world problems often involve complex objective structures that resist distillation into reinforcement learning environments with a single objective. Operation costs must be balanced with multi-dimensional task performance and end-states' effects on future availability, all while ensuring safety for other agents in the environment and the reinforcement learning agent itself. System redundancy through secondary backup controllers has proven to be an effective method to ensure safety in real-world applications where the risk of violating constraints is extremely high. In this work, we investigate the utility of a stacked, continuous-control variation of universal successor feature approximation (USFA) adapted for soft actor-critic (SAC) and coupled with a suite of secondary safety controllers, which we call stacked USFA for safety (SUSFAS). Our method improves performance on secondary objectives compared to SAC baselines using an intervening secondary controller such as a runtime assurance (RTA) controller.

Hybrid dynamical type theories for navigation

We present a hybrid dynamical type theory equipped with useful primitives for organizing and proving safety of navigational control algorithms. This type theory combines the framework of Fu--Kishida--Selinger for constructing linear dependent type theories from state-parameter fibrations with previous work on categories of hybrid systems under sequential composition. We also define a conjectural embedding of a fragment of linear-time temporal logic within our type theory, with the goal of obtaining interoperability with existing state-of-the-art tools for automatic controller synthesis from formal task specifications. As a case study, we use the type theory to organize and prove safety properties for an obstacle-avoiding navigation algorithm of Arslan--Koditschek as implemented by Vasilopoulos. Finally, we speculate on extensions of the type theory to deal with conjugacies between model and physical spaces, as well as hierarchical template-anchor relationships.

Formal composition of hybrid systems

We develop a compositional framework for formal synthesis of hybrid systems using the language of category theory. More specifically, we provide mutually compatible tools for hierarchical, sequential, and independent parallel composition. In our framework, hierarchies of hybrid systems correspond to template-anchor pairs, which we model as spans of subdividing and embedding semiconjugacies. Hierarchical composition of template-anchor pairs corresponds to the composition of spans via pullback. To model sequential composition, we introduce "directed hybrid systems," each of which flows from an initial subsystem to a final subsystem in a Conley-theoretic sense. Sequential composition of directed systems is given by a pushout of graph embeddings, rewriting the continuous dynamics of the overlapping subsystem to prioritize the second directed system. Independent parallel composition corresponds to a categorical product with respect to semiconjugacy. To formalize the compatibility of these three types of composition, we construct a vertically cartesian double category of hybrid systems where the vertical morphisms are semiconjugacies, and the horizontal morphisms are directed hybrid systems.

Functorial Hierarchical Clustering with Overlaps

This work draws inspiration from three important sources of research on dissimilarity-based clustering and intertwines those three threads into a consistent principled functorial theory of clustering. Those three are the overlapping clustering of Jardine and Sibson, the functorial approach of Carlsson and M\'{e}moli to partition-based clustering, and the Isbell/Dress school's study of injective envelopes. Carlsson and M\'{e}moli introduce the idea of viewing clustering methods as functors from a category of metric spaces to a category of clusters, with functoriality subsuming many desirable properties. Our first series of results extends their theory of functorial clustering schemes to methods that allow overlapping clusters in the spirit of Jardine and Sibson. This obviates some of the unpleasant effects of chaining that occur, for example with single-linkage clustering. We prove an equivalence between these general overlapping clustering functors and projections of weight spaces to what we term clustering domains, by focusing on the order structure determined by the morphisms. As a specific application of this machinery, we are able to prove that there are no functorial projections to cut metrics, or even to tree metrics. Finally, although we focus less on the construction of clustering methods (clustering domains) derived from injective envelopes, we lay out some preliminary results, that hopefully will give a feel for how the third leg of the stool comes into play.

Consistency constraints for overlapping data clustering

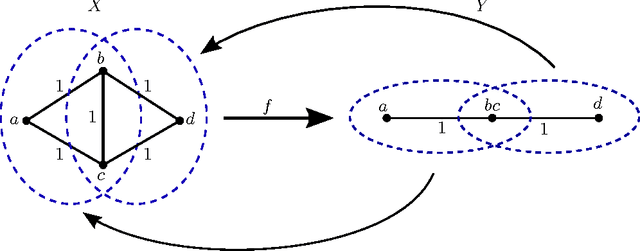
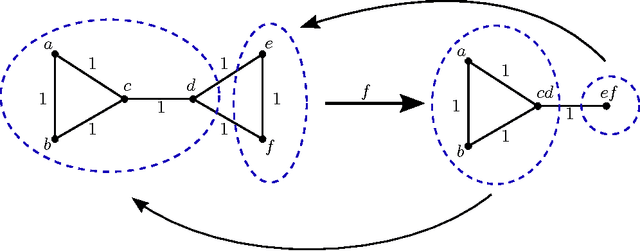
We examine overlapping clustering schemes with functorial constraints, in the spirit of Carlsson--Memoli. This avoids issues arising from the chaining required by partition-based methods. Our principal result shows that any clustering functor is naturally constrained to refine single-linkage clusters and be refined by maximal-linkage clusters. We work in the context of metric spaces with non-expansive maps, which is appropriate for modeling data processing which does not increase information content.