Peter F. Stiller
Formal composition of hybrid systems
Nov 04, 2019
Abstract:We develop a compositional framework for formal synthesis of hybrid systems using the language of category theory. More specifically, we provide mutually compatible tools for hierarchical, sequential, and independent parallel composition. In our framework, hierarchies of hybrid systems correspond to template-anchor pairs, which we model as spans of subdividing and embedding semiconjugacies. Hierarchical composition of template-anchor pairs corresponds to the composition of spans via pullback. To model sequential composition, we introduce "directed hybrid systems," each of which flows from an initial subsystem to a final subsystem in a Conley-theoretic sense. Sequential composition of directed systems is given by a pushout of graph embeddings, rewriting the continuous dynamics of the overlapping subsystem to prioritize the second directed system. Independent parallel composition corresponds to a categorical product with respect to semiconjugacy. To formalize the compatibility of these three types of composition, we construct a vertically cartesian double category of hybrid systems where the vertical morphisms are semiconjugacies, and the horizontal morphisms are directed hybrid systems.
Functorial Hierarchical Clustering with Overlaps
Aug 14, 2018
Abstract:This work draws inspiration from three important sources of research on dissimilarity-based clustering and intertwines those three threads into a consistent principled functorial theory of clustering. Those three are the overlapping clustering of Jardine and Sibson, the functorial approach of Carlsson and M\'{e}moli to partition-based clustering, and the Isbell/Dress school's study of injective envelopes. Carlsson and M\'{e}moli introduce the idea of viewing clustering methods as functors from a category of metric spaces to a category of clusters, with functoriality subsuming many desirable properties. Our first series of results extends their theory of functorial clustering schemes to methods that allow overlapping clusters in the spirit of Jardine and Sibson. This obviates some of the unpleasant effects of chaining that occur, for example with single-linkage clustering. We prove an equivalence between these general overlapping clustering functors and projections of weight spaces to what we term clustering domains, by focusing on the order structure determined by the morphisms. As a specific application of this machinery, we are able to prove that there are no functorial projections to cut metrics, or even to tree metrics. Finally, although we focus less on the construction of clustering methods (clustering domains) derived from injective envelopes, we lay out some preliminary results, that hopefully will give a feel for how the third leg of the stool comes into play.
* Minor revisions. 24 pages, 1 figure
Consistency constraints for overlapping data clustering
Aug 15, 2016
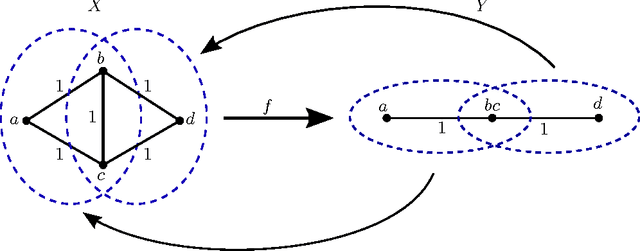
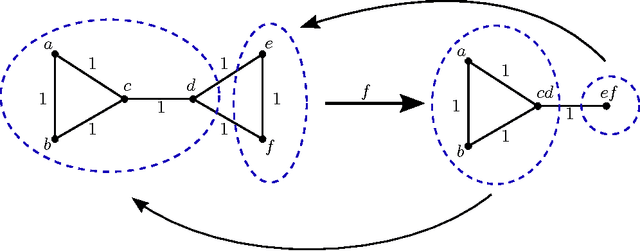
Abstract:We examine overlapping clustering schemes with functorial constraints, in the spirit of Carlsson--Memoli. This avoids issues arising from the chaining required by partition-based methods. Our principal result shows that any clustering functor is naturally constrained to refine single-linkage clusters and be refined by maximal-linkage clusters. We work in the context of metric spaces with non-expansive maps, which is appropriate for modeling data processing which does not increase information content.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge