Dan P. Guralnik
Iterated Belief Revision Under Resource Constraints: Logic as Geometry
Dec 20, 2018



Abstract:We propose a variant of iterated belief revision designed for settings with limited computational resources, such as mobile autonomous robots. The proposed memory architecture---called the {\em universal memory architecture} (UMA)---maintains an epistemic state in the form of a system of default rules similar to those studied by Pearl and by Goldszmidt and Pearl (systems $Z$ and $Z^+$). A duality between the category of UMA representations and the category of the corresponding model spaces, extending the Sageev-Roller duality between discrete poc sets and discrete median algebras provides a two-way dictionary from inference to geometry, leading to immense savings in computation, at a cost in the quality of representation that can be quantified in terms of topological invariants. Moreover, the same framework naturally enables comparisons between different model spaces, making it possible to analyze the deficiencies of one model space in comparison to others. This paper develops the formalism underlying UMA, analyzes the complexity of maintenance and inference operations in UMA, and presents some learning guarantees for different UMA-based learners. Finally, we present simulation results to illustrate the viability of the approach, and close with a discussion of the strengths, weaknesses, and potential development of UMA-based learners.
Functorial Hierarchical Clustering with Overlaps
Aug 14, 2018
Abstract:This work draws inspiration from three important sources of research on dissimilarity-based clustering and intertwines those three threads into a consistent principled functorial theory of clustering. Those three are the overlapping clustering of Jardine and Sibson, the functorial approach of Carlsson and M\'{e}moli to partition-based clustering, and the Isbell/Dress school's study of injective envelopes. Carlsson and M\'{e}moli introduce the idea of viewing clustering methods as functors from a category of metric spaces to a category of clusters, with functoriality subsuming many desirable properties. Our first series of results extends their theory of functorial clustering schemes to methods that allow overlapping clusters in the spirit of Jardine and Sibson. This obviates some of the unpleasant effects of chaining that occur, for example with single-linkage clustering. We prove an equivalence between these general overlapping clustering functors and projections of weight spaces to what we term clustering domains, by focusing on the order structure determined by the morphisms. As a specific application of this machinery, we are able to prove that there are no functorial projections to cut metrics, or even to tree metrics. Finally, although we focus less on the construction of clustering methods (clustering domains) derived from injective envelopes, we lay out some preliminary results, that hopefully will give a feel for how the third leg of the stool comes into play.
* Minor revisions. 24 pages, 1 figure
Statistical Properties of the Single Linkage Hierarchical Clustering Estimator
Sep 01, 2016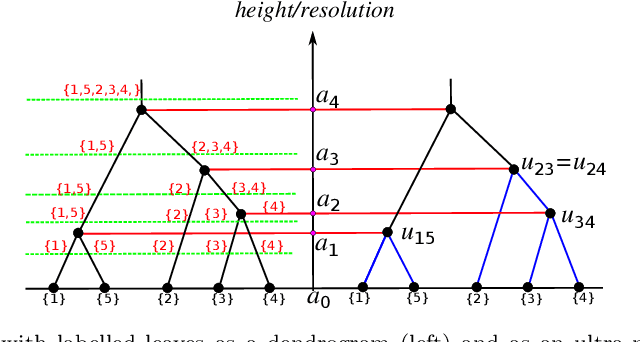
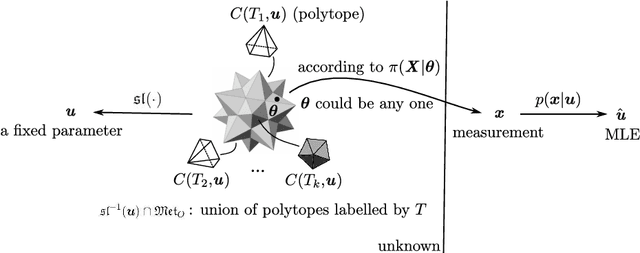
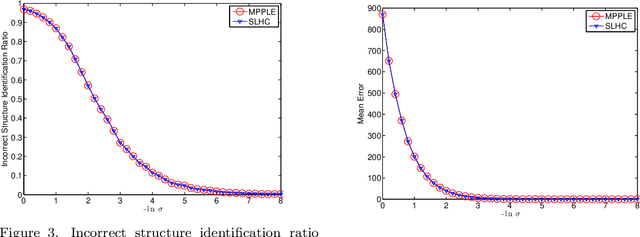
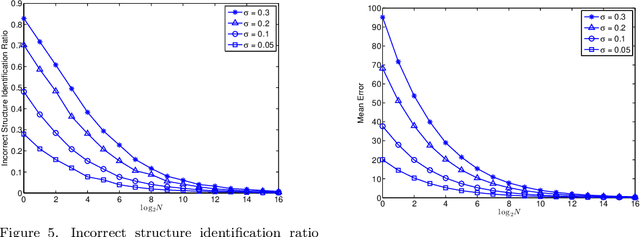
Abstract:Distance-based hierarchical clustering (HC) methods are widely used in unsupervised data analysis but few authors take account of uncertainty in the distance data. We incorporate a statistical model of the uncertainty through corruption or noise in the pairwise distances and investigate the problem of estimating the HC as unknown parameters from measurements. Specifically, we focus on single linkage hierarchical clustering (SLHC) and study its geometry. We prove that under fairly reasonable conditions on the probability distribution governing measurements, SLHC is equivalent to maximum partial profile likelihood estimation (MPPLE) with some of the information contained in the data ignored. At the same time, we show that direct evaluation of SLHC on maximum likelihood estimation (MLE) of pairwise distances yields a consistent estimator. Consequently, a full MLE is expected to perform better than SLHC in getting the correct HC results for the ground truth metric.
Consistency constraints for overlapping data clustering
Aug 15, 2016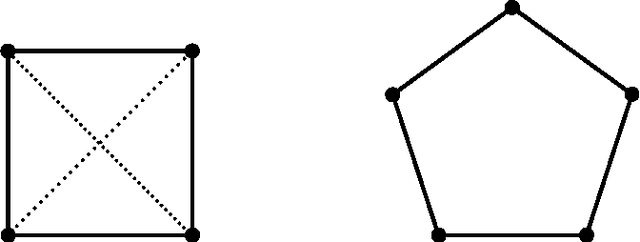
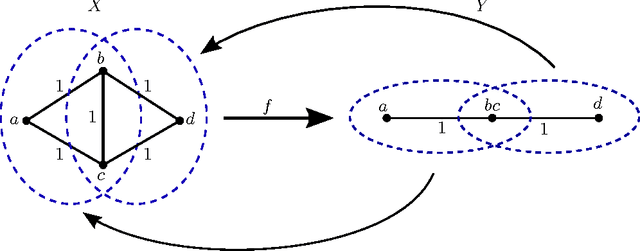
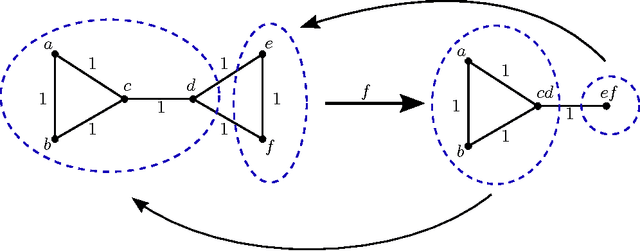
Abstract:We examine overlapping clustering schemes with functorial constraints, in the spirit of Carlsson--Memoli. This avoids issues arising from the chaining required by partition-based methods. Our principal result shows that any clustering functor is naturally constrained to refine single-linkage clusters and be refined by maximal-linkage clusters. We work in the context of metric spaces with non-expansive maps, which is appropriate for modeling data processing which does not increase information content.
Maximum Likelihood Estimation for Single Linkage Hierarchical Clustering
Nov 25, 2015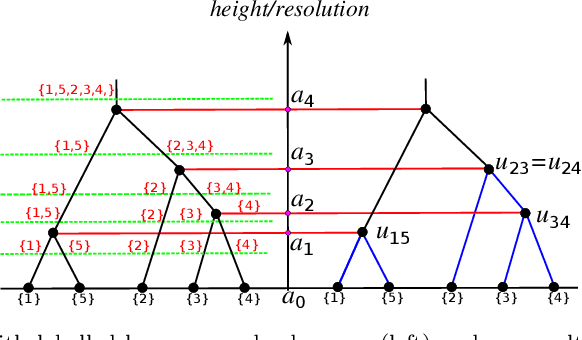
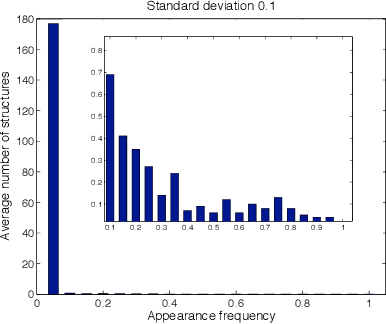
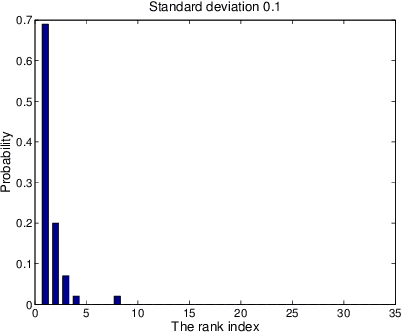
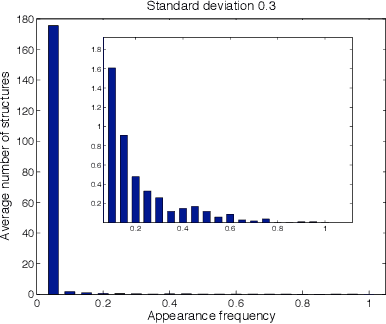
Abstract:We derive a statistical model for estimation of a dendrogram from single linkage hierarchical clustering (SLHC) that takes account of uncertainty through noise or corruption in the measurements of separation of data. Our focus is on just the estimation of the hierarchy of partitions afforded by the dendrogram, rather than the heights in the latter. The concept of estimating this "dendrogram structure'' is introduced, and an approximate maximum likelihood estimator (MLE) for the dendrogram structure is described. These ideas are illustrated by a simple Monte Carlo simulation that, at least for small data sets, suggests the method outperforms SLHC in the presence of noise.
Coordinated Robot Navigation via Hierarchical Clustering
Jul 06, 2015



Abstract:We introduce the use of hierarchical clustering for relaxed, deterministic coordination and control of multiple robots. Traditionally an unsupervised learning method, hierarchical clustering offers a formalism for identifying and representing spatially cohesive and segregated robot groups at different resolutions by relating the continuous space of configurations to the combinatorial space of trees. We formalize and exploit this relation, developing computationally effective reactive algorithms for navigating through the combinatorial space in concert with geometric realizations for a particular choice of hierarchical clustering method. These constructions yield computationally effective vector field planners for both hierarchically invariant as well as transitional navigation in the configuration space. We apply these methods to the centralized coordination and control of $n$ perfectly sensed and actuated Euclidean spheres in a $d$-dimensional ambient space (for arbitrary $n$ and $d$). Given a desired configuration supporting a desired hierarchy, we construct a hybrid controller which is quadratic in $n$ and algebraic in $d$ and prove that its execution brings all but a measure zero set of initial configurations to the desired goal with the guarantee of no collisions along the way.
Universal Memory Architectures for Autonomous Machines
Feb 21, 2015



Abstract:We propose a self-organizing memory architecture for perceptual experience, capable of supporting autonomous learning and goal-directed problem solving in the absence of any prior information about the agent's environment. The architecture is simple enough to ensure (1) a quadratic bound (in the number of available sensors) on space requirements, and (2) a quadratic bound on the time-complexity of the update-execute cycle. At the same time, it is sufficiently complex to provide the agent with an internal representation which is (3) minimal among all representations of its class which account for every sensory equivalence class subject to the agent's belief state; (4) capable, in principle, of recovering the homotopy type of the system's state space; (5) learnable with arbitrary precision through a random application of the available actions. The provable properties of an effectively trained memory structure exploit a duality between weak poc sets -- a symbolic (discrete) representation of subset nesting relations -- and non-positively curved cubical complexes, whose rich convexity theory underlies the planning cycle of the proposed architecture.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge