Fast and Safe Path-Following Control using a State-Dependent Directional Metric

This paper considers the problem of fast and safe autonomous navigation in partially known environments. Our main contribution is a control policy design based on ellipsoidal trajectory bounds obtained from a quadratic state-dependent distance metric. The ellipsoidal bounds are used to embed directional preference in the control design, leading to system behavior that is adapted to the local environment geometry, carefully considering medial obstacles while paying less attention to lateral ones. We use a virtual reference governor system to adaptively follow a desired navigation path, slowing down when system safety may be violated and speeding up otherwise. The resulting controller is able to navigate complex environments faster than common Euclidean-norm and Lyapunov-function-based designs, while retaining stability and collision avoidance guarantees.

Probabilistically Safe Corridors to Guide Sampling-Based Motion Planning

In this paper, we introduce a new probabilistically safe local steering primitive for sampling-based motion planning in complex high-dimensional configuration spaces. Our local steering procedure is based on a new notion of a convex probabilistically safe corridor that is constructed around a configuration using tangent hyperplanes of confidence ellipsoids of Gaussian mixture models learned from prior collision history. Accordingly, we propose to expand a random motion planning graph towards a sample goal using its projection onto probabilistically safe corridors, which efficiently exploits the local geometry of configuration spaces for selecting proper steering direction and adapting steering stepsize. We observe that the proposed local steering procedure generates effective steering motion around difficult regions of configuration spaces, such as narrow passages, while minimizing collision likelihood. We evaluate the proposed steering method with randomized motion planners in a number of planning scenarios, both in simulation and on a physical 7DoF robot arm, demonstrating the effectiveness of our safety guided local planner over the standard straight-line planner.

Technical Report: Sensor-Based Reactive Symbolic Planning in Partially Known Environments

This paper considers the problem of completing assemblies of passive objects in nonconvex environments, cluttered with convex obstacles of unknown position, shape and size that satisfy a specific separation assumption. A differential drive robot equipped with a gripper and a LIDAR sensor, capable of perceiving its environment only locally, is used to position the passive objects in a desired configuration. The method combines the virtues of a deliberative planner generating high-level, symbolic commands, with the formal guarantees of convergence and obstacle avoidance of a reactive planner that requires little onboard computation and is used online. The validity of the proposed method is verified both with formal proofs and numerical simulations.

Voronoi-Based Coverage Control of Heterogeneous Disk-Shaped Robots

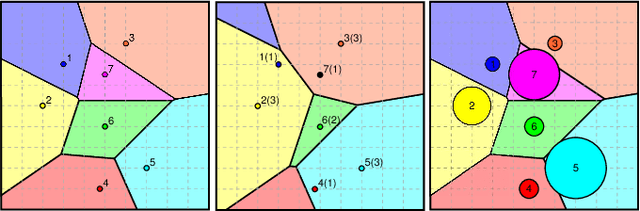
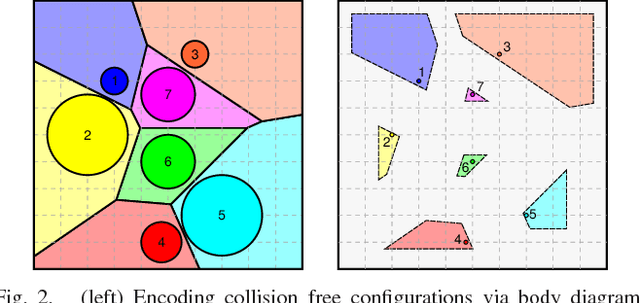
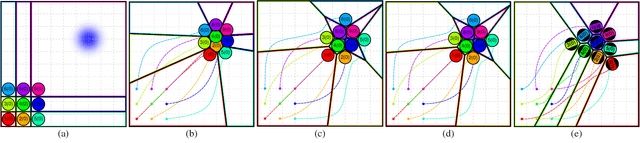
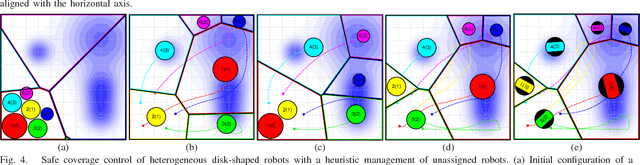
In distributed mobile sensing applications, networks of agents that are heterogeneous respecting both actuation as well as body and sensory footprint are often modelled by recourse to power diagrams --- generalized Voronoi diagrams with additive weights. In this paper we adapt the body power diagram to introduce its "free subdiagram," generating a vector field planner that solves the combined sensory coverage and collision avoidance problem via continuous evaluation of an associated constrained optimization problem. We propose practical extensions (a heuristic congestion manager that speeds convergence and a lift of the point particle controller to the more practical differential drive kinematics) that maintain the convergence and collision guarantees.

Coordinated Robot Navigation via Hierarchical Clustering

We introduce the use of hierarchical clustering for relaxed, deterministic coordination and control of multiple robots. Traditionally an unsupervised learning method, hierarchical clustering offers a formalism for identifying and representing spatially cohesive and segregated robot groups at different resolutions by relating the continuous space of configurations to the combinatorial space of trees. We formalize and exploit this relation, developing computationally effective reactive algorithms for navigating through the combinatorial space in concert with geometric realizations for a particular choice of hierarchical clustering method. These constructions yield computationally effective vector field planners for both hierarchically invariant as well as transitional navigation in the configuration space. We apply these methods to the centralized coordination and control of $n$ perfectly sensed and actuated Euclidean spheres in a $d$-dimensional ambient space (for arbitrary $n$ and $d$). Given a desired configuration supporting a desired hierarchy, we construct a hybrid controller which is quadratic in $n$ and algebraic in $d$ and prove that its execution brings all but a measure zero set of initial configurations to the desired goal with the guarantee of no collisions along the way.

Anytime Hierarchical Clustering

We propose a new anytime hierarchical clustering method that iteratively transforms an arbitrary initial hierarchy on the configuration of measurements along a sequence of trees we prove for a fixed data set must terminate in a chain of nested partitions that satisfies a natural homogeneity requirement. Each recursive step re-edits the tree so as to improve a local measure of cluster homogeneity that is compatible with a number of commonly used (e.g., single, average, complete) linkage functions. As an alternative to the standard batch algorithms, we present numerical evidence to suggest that appropriate adaptations of this method can yield decentralized, scalable algorithms suitable for distributed/parallel computation of clustering hierarchies and online tracking of clustering trees applicable to large, dynamically changing databases and anomaly detection.