Statistical Properties of the Single Linkage Hierarchical Clustering Estimator

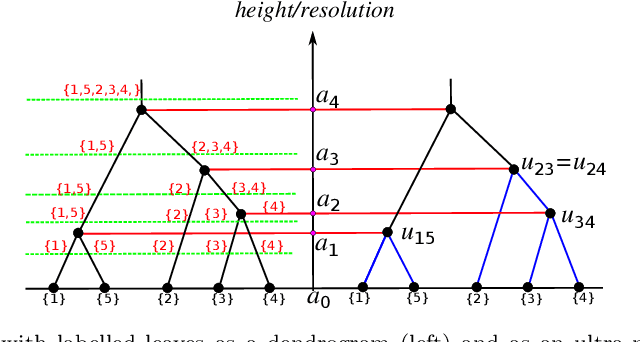
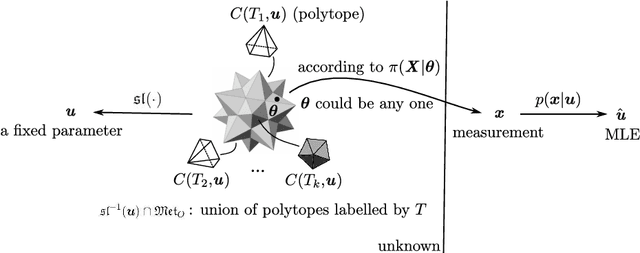
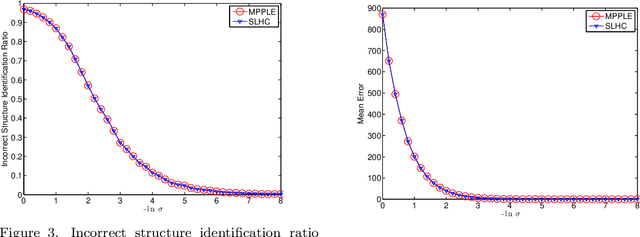
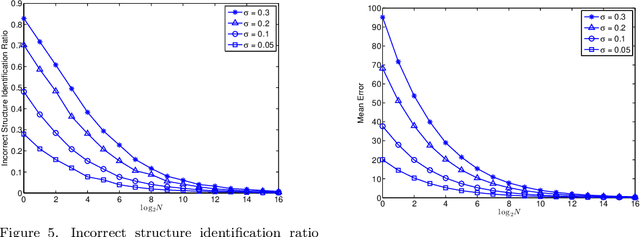
Distance-based hierarchical clustering (HC) methods are widely used in unsupervised data analysis but few authors take account of uncertainty in the distance data. We incorporate a statistical model of the uncertainty through corruption or noise in the pairwise distances and investigate the problem of estimating the HC as unknown parameters from measurements. Specifically, we focus on single linkage hierarchical clustering (SLHC) and study its geometry. We prove that under fairly reasonable conditions on the probability distribution governing measurements, SLHC is equivalent to maximum partial profile likelihood estimation (MPPLE) with some of the information contained in the data ignored. At the same time, we show that direct evaluation of SLHC on maximum likelihood estimation (MLE) of pairwise distances yields a consistent estimator. Consequently, a full MLE is expected to perform better than SLHC in getting the correct HC results for the ground truth metric.

Maximum Likelihood Estimation for Single Linkage Hierarchical Clustering

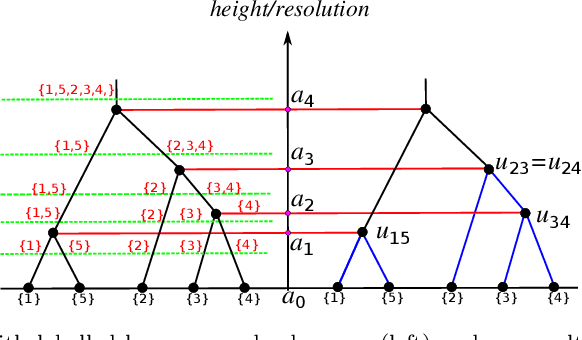
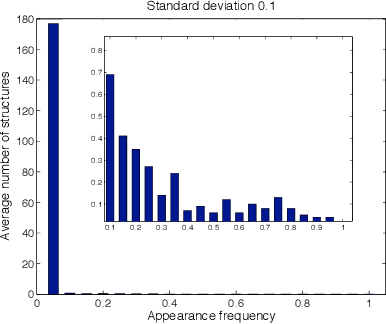
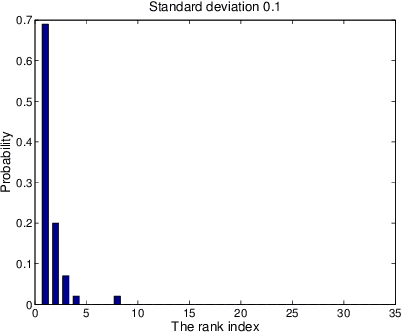
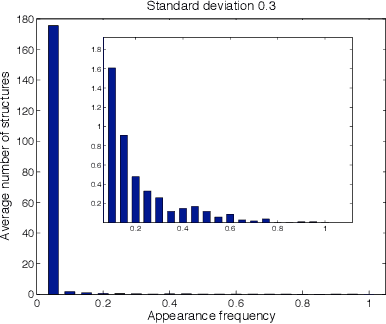
We derive a statistical model for estimation of a dendrogram from single linkage hierarchical clustering (SLHC) that takes account of uncertainty through noise or corruption in the measurements of separation of data. Our focus is on just the estimation of the hierarchy of partitions afforded by the dendrogram, rather than the heights in the latter. The concept of estimating this "dendrogram structure'' is introduced, and an approximate maximum likelihood estimator (MLE) for the dendrogram structure is described. These ideas are illustrated by a simple Monte Carlo simulation that, at least for small data sets, suggests the method outperforms SLHC in the presence of noise.