Multi-Action Restless Bandits with Weakly Coupled Constraints: Simultaneous Learning and Control

We study a system with finitely many groups of multi-action bandit processes, each of which is a Markov decision process (MDP) with finite state and action spaces and potentially different transition matrices when taking different actions. The bandit processes of the same group share the same state and action spaces and, given the same action that is taken, the same transition matrix. All the bandit processes across various groups are subject to multiple weakly coupled constraints over their state and action variables. Unlike the past studies that focused on the offline case, we consider the online case without assuming full knowledge of transition matrices and reward functions a priori and propose an effective scheme that enables simultaneous learning and control. We prove the convergence of the relevant processes in both the timeline and the number of the bandit processes, referred to as the convergence in the time and the magnitude dimensions. Moreover, we prove that the relevant processes converge exponentially fast in the magnitude dimension, leading to exponentially diminishing performance deviation between the proposed online algorithms and offline optimality.

Gravity aided navigation using Viterbi map matching algorithm

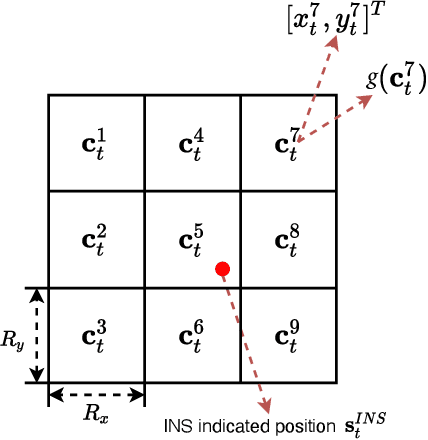
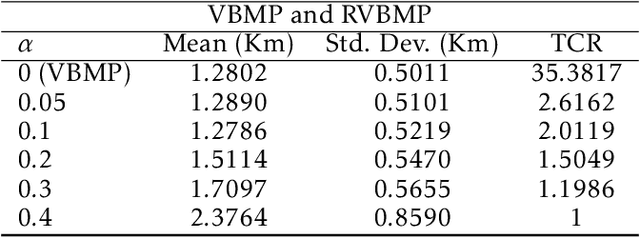
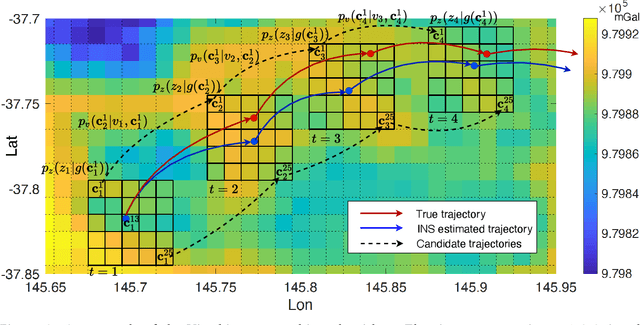
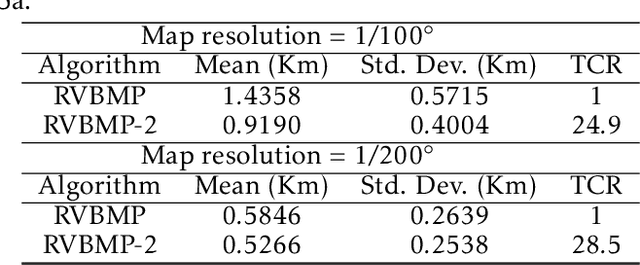
In GNSS-denied environments, aiding a vehicle's inertial navigation system (INS) is crucial to reducing the accumulated navigation drift caused by sensor errors (e.g. bias and noise). One potential solution is to use measurements of gravity as an aiding source. The measurements are matched to a geo-referenced map of Earth's gravity in order to estimate the vehicle's position. In this paper, we propose a novel formulation of the map matching problem using a hidden Markov model (HMM). Specifically, we treat the spatial cells of the map as the hidden states of the HMM and present a Viterbi style algorithm to estimate the most likely sequence of states, i.e. most likely sequence of vehicle positions, that results in the sequence of observed gravity measurements. Using a realistic gravity map, we demonstrate the accuracy of our Viterbi map matching algorithm in a navigation scenario and illustrate its robustness compared to existing methods.

Probabilistic Map Matching for Robust Inertial Navigation Aiding

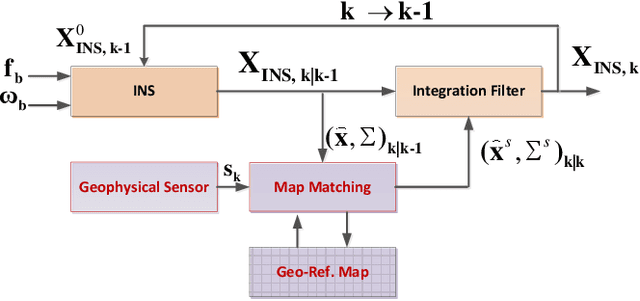
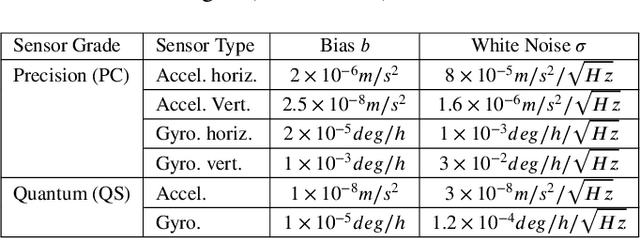
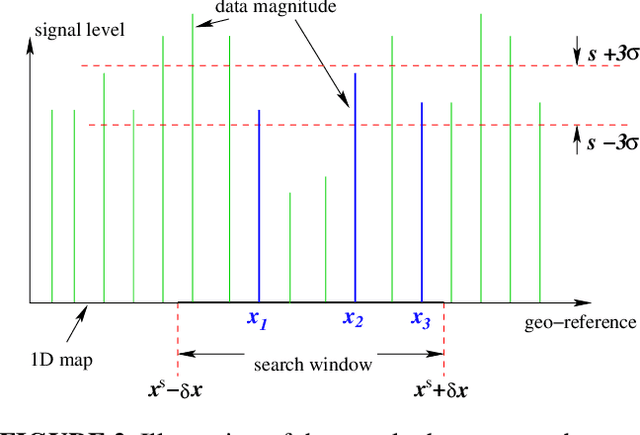
Robust aiding of inertial navigation systems in GNSS-denied environments is critical for the removal of accumulated navigation error caused by the drift and bias inherent in inertial sensors. One way to perform such an aiding uses matching of geophysical measurements, such as gravimetry, gravity gradiometry or magnetometry, with a known geo-referenced map. Although simple in concept, this map matching procedure is challenging: the measurements themselves are noisy; their associated spatial location is uncertain; and the measurements may match multiple points within the map (i.e. non-unique solution). In this paper, we propose a probabilistic multiple hypotheses tracker to solve the map matching problem and allow robust inertial navigation aiding. Our approach addresses the problem both locally, via probabilistic data association, and temporally by incorporating the underlying platform kinematic constraints into the tracker. The map matching output is then integrated into the navigation system using an unscented Kalman filter. Additionally, we present a statistical measure of local map information density -- the map feature variability -- and use it to weight the output covariance of the proposed algorithm. The effectiveness and robustness of the proposed algorithm are demonstrated using a navigation scenario involving gravitational map matching.

Statistical Properties of the Single Linkage Hierarchical Clustering Estimator

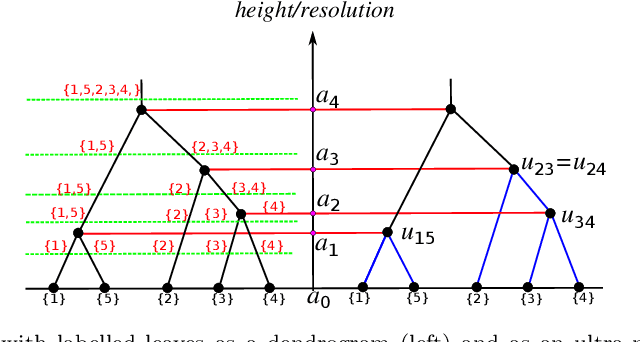
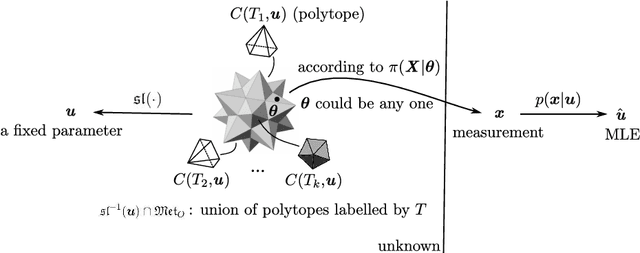
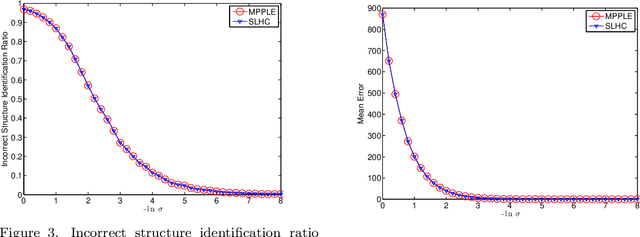
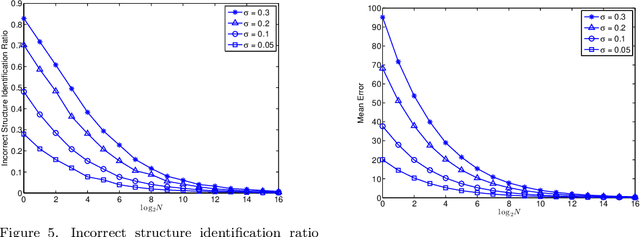
Distance-based hierarchical clustering (HC) methods are widely used in unsupervised data analysis but few authors take account of uncertainty in the distance data. We incorporate a statistical model of the uncertainty through corruption or noise in the pairwise distances and investigate the problem of estimating the HC as unknown parameters from measurements. Specifically, we focus on single linkage hierarchical clustering (SLHC) and study its geometry. We prove that under fairly reasonable conditions on the probability distribution governing measurements, SLHC is equivalent to maximum partial profile likelihood estimation (MPPLE) with some of the information contained in the data ignored. At the same time, we show that direct evaluation of SLHC on maximum likelihood estimation (MLE) of pairwise distances yields a consistent estimator. Consequently, a full MLE is expected to perform better than SLHC in getting the correct HC results for the ground truth metric.

Maximum Likelihood Estimation for Single Linkage Hierarchical Clustering

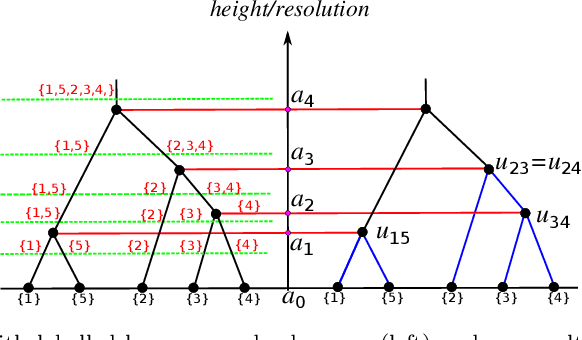
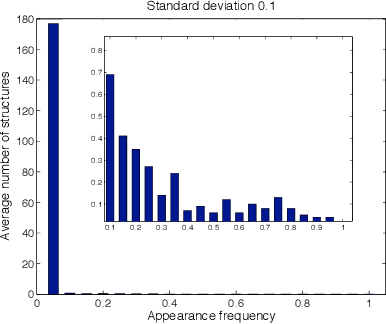
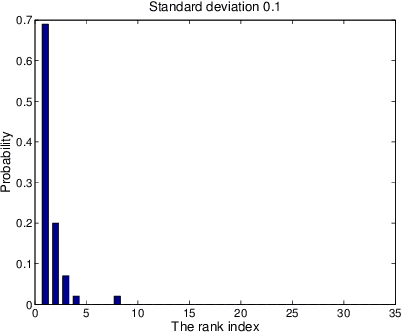
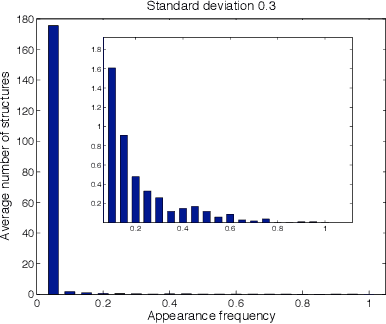
We derive a statistical model for estimation of a dendrogram from single linkage hierarchical clustering (SLHC) that takes account of uncertainty through noise or corruption in the measurements of separation of data. Our focus is on just the estimation of the hierarchy of partitions afforded by the dendrogram, rather than the heights in the latter. The concept of estimating this "dendrogram structure'' is introduced, and an approximate maximum likelihood estimator (MLE) for the dendrogram structure is described. These ideas are illustrated by a simple Monte Carlo simulation that, at least for small data sets, suggests the method outperforms SLHC in the presence of noise.