Thomas Gebhart
Sheaf theory: from deep geometry to deep learning
Feb 21, 2025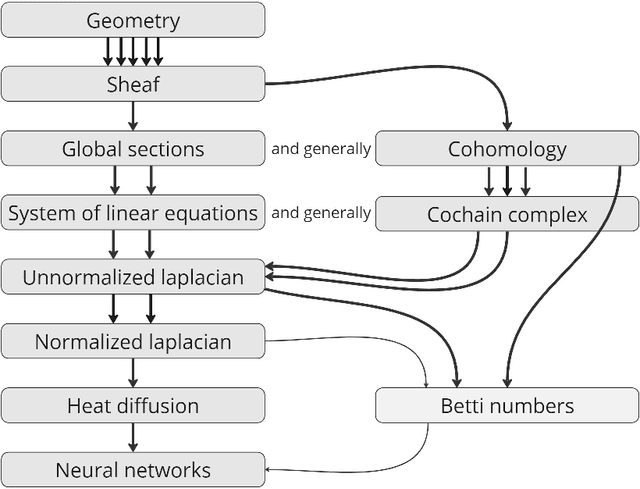
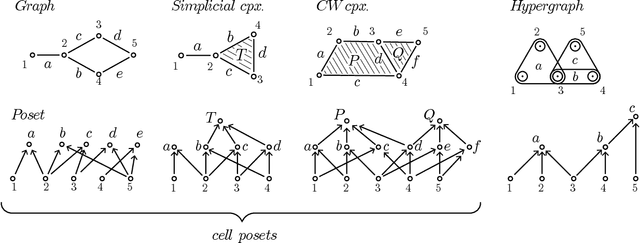
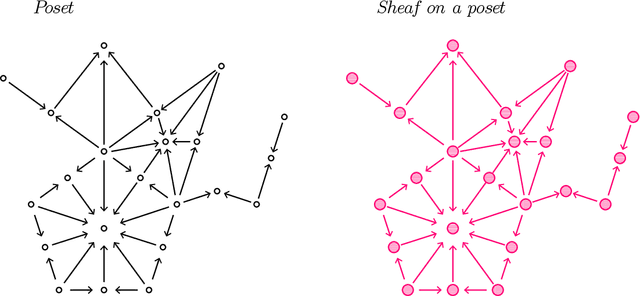
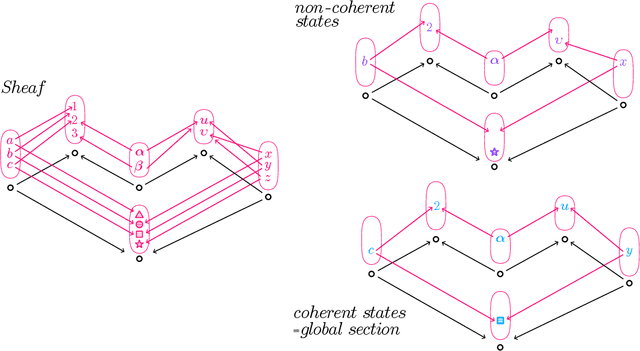
Abstract:This paper provides an overview of the applications of sheaf theory in deep learning, data science, and computer science in general. The primary text of this work serves as a friendly introduction to applied and computational sheaf theory accessible to those with modest mathematical familiarity. We describe intuitions and motivations underlying sheaf theory shared by both theoretical researchers and practitioners, bridging classical mathematical theory and its more recent implementations within signal processing and deep learning. We observe that most notions commonly considered specific to cellular sheaves translate to sheaves on arbitrary posets, providing an interesting avenue for further generalization of these methods in applications, and we present a new algorithm to compute sheaf cohomology on arbitrary finite posets in response. By integrating classical theory with recent applications, this work reveals certain blind spots in current machine learning practices. We conclude with a list of problems related to sheaf-theoretic applications that we find mathematically insightful and practically instructive to solve. To ensure the exposition of sheaf theory is self-contained, a rigorous mathematical introduction is provided in appendices which moves from an introduction of diagrams and sheaves to the definition of derived functors, higher order cohomology, sheaf Laplacians, sheaf diffusion, and interconnections of these subjects therein.
ICML Topological Deep Learning Challenge 2024: Beyond the Graph Domain
Sep 08, 2024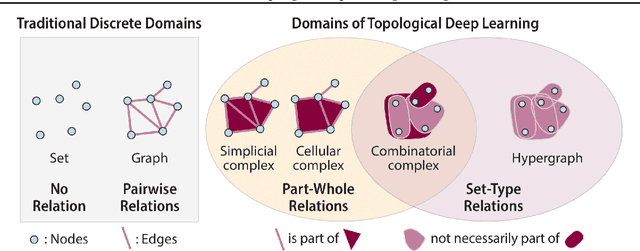
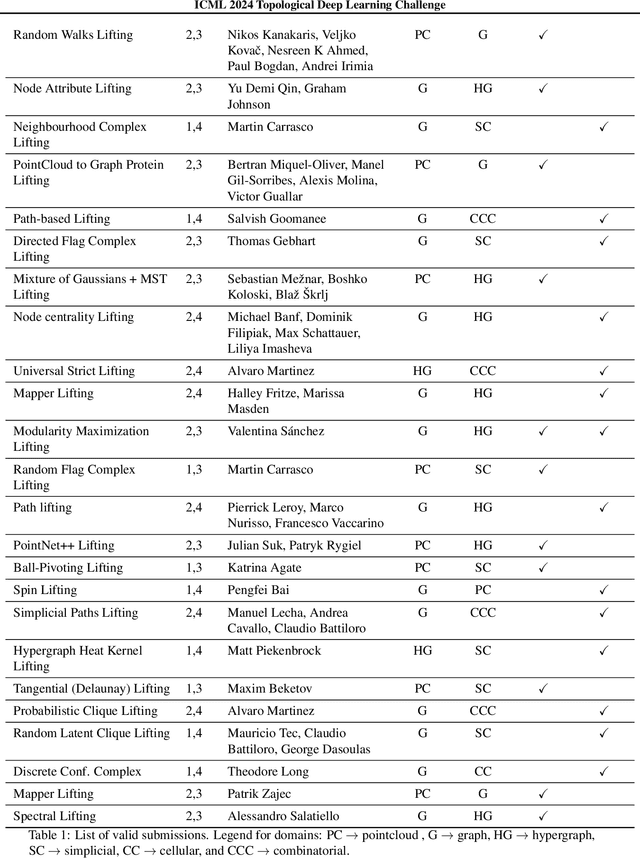
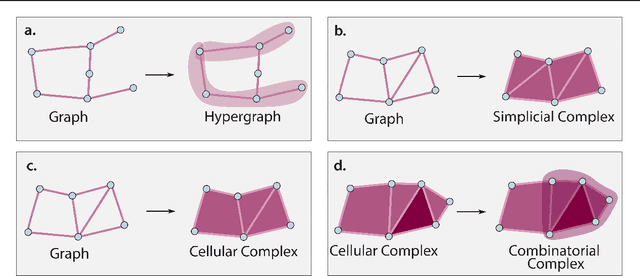
Abstract:This paper describes the 2nd edition of the ICML Topological Deep Learning Challenge that was hosted within the ICML 2024 ELLIS Workshop on Geometry-grounded Representation Learning and Generative Modeling (GRaM). The challenge focused on the problem of representing data in different discrete topological domains in order to bridge the gap between Topological Deep Learning (TDL) and other types of structured datasets (e.g. point clouds, graphs). Specifically, participants were asked to design and implement topological liftings, i.e. mappings between different data structures and topological domains --like hypergraphs, or simplicial/cell/combinatorial complexes. The challenge received 52 submissions satisfying all the requirements. This paper introduces the main scope of the challenge, and summarizes the main results and findings.
Extending Transductive Knowledge Graph Embedding Models for Inductive Logical Relational Inference
Sep 07, 2023Abstract:Many downstream inference tasks for knowledge graphs, such as relation prediction, have been handled successfully by knowledge graph embedding techniques in the transductive setting. To address the inductive setting wherein new entities are introduced into the knowledge graph at inference time, more recent work opts for models which learn implicit representations of the knowledge graph through a complex function of a network's subgraph structure, often parametrized by graph neural network architectures. These come at the cost of increased parametrization, reduced interpretability and limited generalization to other downstream inference tasks. In this work, we bridge the gap between traditional transductive knowledge graph embedding approaches and more recent inductive relation prediction models by introducing a generalized form of harmonic extension which leverages representations learned through transductive embedding methods to infer representations of new entities introduced at inference time as in the inductive setting. This harmonic extension technique provides the best such approximation, can be implemented via an efficient iterative scheme, and can be employed to answer a family of conjunctive logical queries over the knowledge graph, further expanding the capabilities of transductive embedding methods. In experiments on a number of large-scale knowledge graph embedding benchmarks, we find that this approach for extending the functionality of transductive knowledge graph embedding models to perform knowledge graph completion and answer logical queries in the inductive setting is competitive with--and in some scenarios outperforms--several state-of-the-art models derived explicitly for such inductive tasks.
Graph Convolutional Networks from the Perspective of Sheaves and the Neural Tangent Kernel
Aug 19, 2022Abstract:Graph convolutional networks are a popular class of deep neural network algorithms which have shown success in a number of relational learning tasks. Despite their success, graph convolutional networks exhibit a number of peculiar features, including a bias towards learning oversmoothed and homophilic functions, which are not easily diagnosed due to the complex nature of these algorithms. We propose to bridge this gap in understanding by studying the neural tangent kernel of sheaf convolutional networks--a topological generalization of graph convolutional networks. To this end, we derive a parameterization of the neural tangent kernel for sheaf convolutional networks which separates the function into two parts: one driven by a forward diffusion process determined by the graph, and the other determined by the composite effect of nodes' activations on the output layer. This geometrically-focused derivation produces a number of immediate insights which we discuss in detail.
Knowledge Sheaves: A Sheaf-Theoretic Framework for Knowledge Graph Embedding
Oct 07, 2021
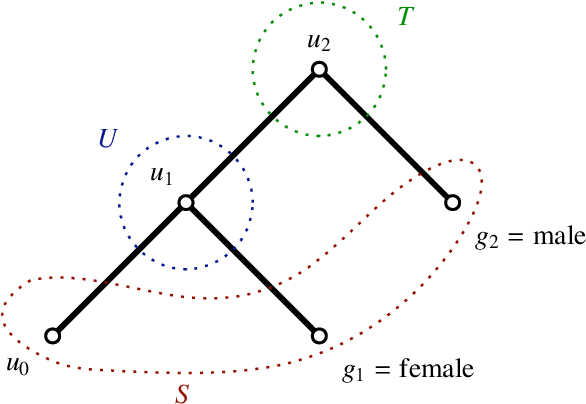


Abstract:Knowledge graph embedding involves learning representations of entities -- the vertices of the graph -- and relations -- the edges of the graph -- such that the resulting representations encode the known factual information represented by the knowledge graph are internally consistent and can be used in the inference of new relations. We show that knowledge graph embedding is naturally expressed in the topological and categorical language of \textit{cellular sheaves}: learning a knowledge graph embedding corresponds to learning a \textit{knowledge sheaf} over the graph, subject to certain constraints. In addition to providing a generalized framework for reasoning about knowledge graph embedding models, this sheaf-theoretic perspective admits the expression of a broad class of prior constraints on embeddings and offers novel inferential capabilities. We leverage the recently developed spectral theory of sheaf Laplacians to understand the local and global consistency of embeddings and develop new methods for reasoning over composite relations through harmonic extension with respect to the sheaf Laplacian. We then implement these ideas to highlight the benefits of the extensions inspired by this new perspective.
A Unified Paths Perspective for Pruning at Initialization
Jan 26, 2021



Abstract:A number of recent approaches have been proposed for pruning neural network parameters at initialization with the goal of reducing the size and computational burden of models while minimally affecting their training dynamics and generalization performance. While each of these approaches have some amount of well-founded motivation, a rigorous analysis of the effect of these pruning methods on network training dynamics and their formal relationship to each other has thus far received little attention. Leveraging recent theoretical approximations provided by the Neural Tangent Kernel, we unify a number of popular approaches for pruning at initialization under a single path-centric framework. We introduce the Path Kernel as the data-independent factor in a decomposition of the Neural Tangent Kernel and show the global structure of the Path Kernel can be computed efficiently. This Path Kernel decomposition separates the architectural effects from the data-dependent effects within the Neural Tangent Kernel, providing a means to predict the convergence dynamics of a network from its architecture alone. We analyze the use of this structure in approximating training and generalization performance of networks in the absence of data across a number of initialization pruning approaches. Observing the relationship between input data and paths and the relationship between the Path Kernel and its natural norm, we additionally propose two augmentations of the SynFlow algorithm for pruning at initialization.
Sheaf Neural Networks
Dec 08, 2020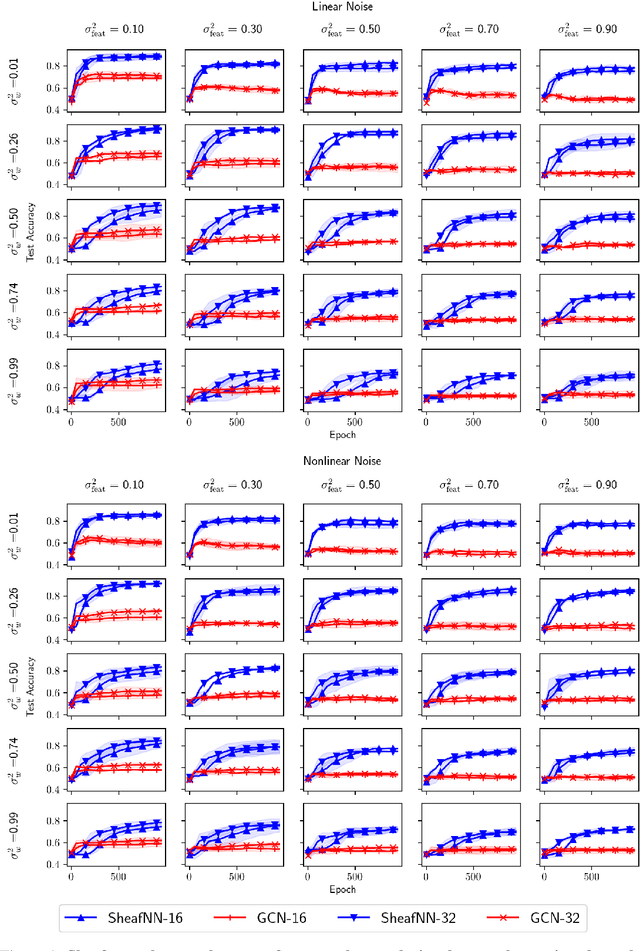
Abstract:We present a generalization of graph convolutional networks by generalizing the diffusion operation underlying this class of graph neural networks. These sheaf neural networks are based on the sheaf Laplacian, a generalization of the graph Laplacian that encodes additional relational structure parameterized by the underlying graph. The sheaf Laplacian and associated matrices provide an extended version of the diffusion operation in graph convolutional networks, providing a proper generalization for domains where relations between nodes are non-constant, asymmetric, and varying in dimension. We show that the resulting sheaf neural networks can outperform graph convolutional networks in domains where relations between nodes are asymmetric and signed.
Path homologies of deep feedforward networks
Oct 16, 2019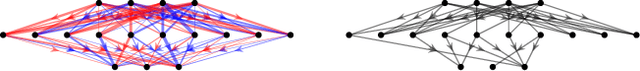
Abstract:We provide a characterization of two types of directed homology for fully-connected, feedforward neural network architectures. These exact characterizations of the directed homology structure of a neural network architecture are the first of their kind. We show that the directed flag homology of deep networks reduces to computing the simplicial homology of the underlying undirected graph, which is explicitly given by Euler characteristic computations. We also show that the path homology of these networks is non-trivial in higher dimensions and depends on the number and size of the layers within the network. These results provide a foundation for investigating homological differences between neural network architectures and their realized structure as implied by their parameters.
Adversarial Examples Target Topological Holes in Deep Networks
Jan 28, 2019



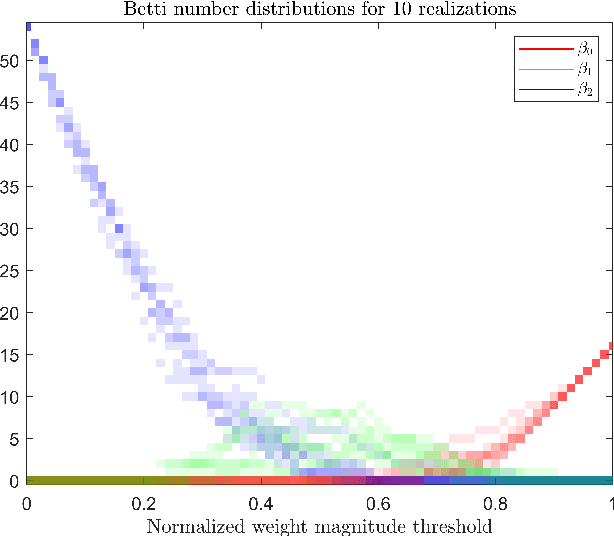
Abstract:It is currently unclear why adversarial examples are easy to construct for deep networks that are otherwise successful with respect to their training domain. However, it is suspected that these adversarial examples lie within some small perturbation from the network's decision boundaries or exist in low-density regions with respect to the training distribution. Using persistent homology, we find that deep networks effectively have ``holes'' in their activation graphs, making them blind to regions of the input space that can be exploited by adversarial examples. These holes are effectively dense in the input space, making it easy to find a perturbed image that can be misclassified. By studying the topology of network activation, we find global patterns in the form of activation subgraphs which can both reliably determine whether an example is adversarial and can recover the true category of the example well above chance, implying that semantic information about the input is embedded globally via the activation pattern in deep networks.
Adversary Detection in Neural Networks via Persistent Homology
Nov 28, 2017



Abstract:We outline a detection method for adversarial inputs to deep neural networks. By viewing neural network computations as graphs upon which information flows from input space to out- put distribution, we compare the differences in graphs induced by different inputs. Specifically, by applying persistent homology to these induced graphs, we observe that the structure of the most persistent subgraphs which generate the first homology group differ between adversarial and unperturbed inputs. Based on this observation, we build a detection algorithm that depends only on the topological information extracted during training. We test our algorithm on MNIST and achieve 98% detection adversary accuracy with F1-score 0.98.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge