Neurosymbolic artificial intelligence via large language models and coherence-driven inference

We devise an algorithm to generate sets of propositions that objectively instantiate graphs that support coherence-driven inference. We then benchmark the ability of large language models (LLMs) to reconstruct coherence graphs from (a straightforward transformation of) propositions expressed in natural language, with promising results from a single prompt to models optimized for reasoning. Combining coherence-driven inference with consistency evaluations by neural models may advance the state of the art in machine cognition.

Prospects for inconsistency detection using large language models and sheaves

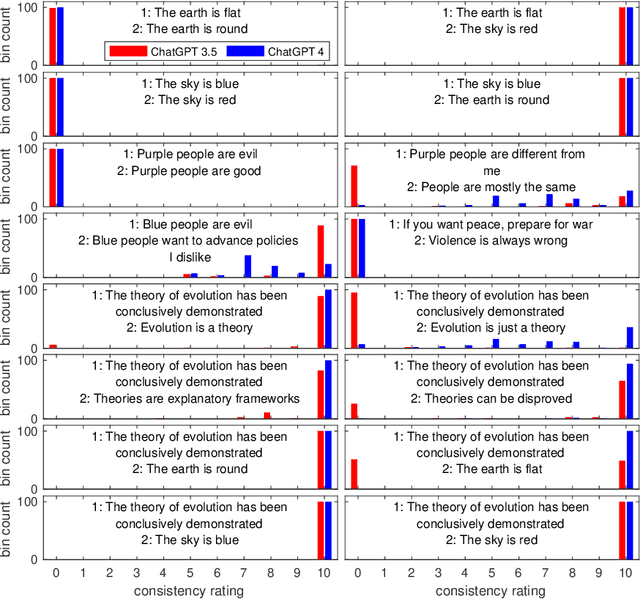
We demonstrate that large language models can produce reasonable numerical ratings of the logical consistency of claims. We also outline a mathematical approach based on sheaf theory for lifting such ratings to hypertexts such as laws, jurisprudence, and social media and evaluating their consistency globally. This approach is a promising avenue to increasing consistency in and of government, as well as to combating mis- and disinformation and related ills.

Diversity Enhancement via Magnitude

Promoting and maintaining diversity of candidate solutions is a key requirement of evolutionary algorithms in general and multi-objective evolutionary algorithms in particular. In this paper, we use the recently developed theory of magnitude to construct a gradient flow and similar notions that systematically manipulate finite subsets of Euclidean space to enhance their diversity, and apply the ideas in service of multi-objective evolutionary algorithms. We demonstrate diversity enhancement on benchmark problems using leading algorithms, and discuss extensions of the framework.

Path homologies of deep feedforward networks

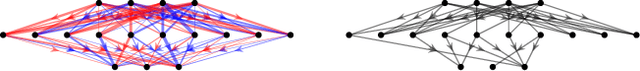
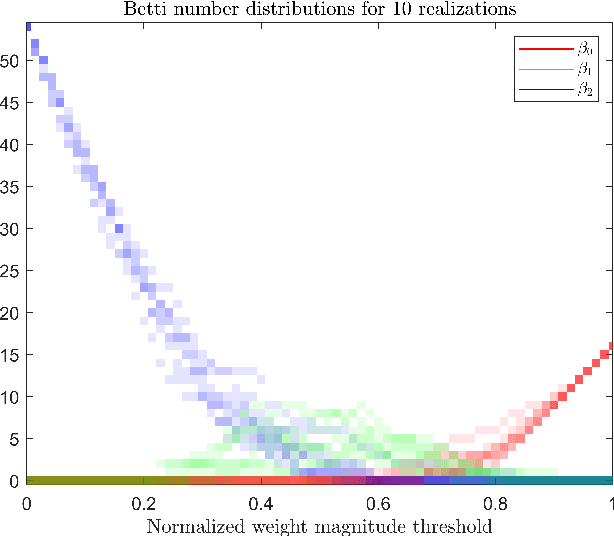
We provide a characterization of two types of directed homology for fully-connected, feedforward neural network architectures. These exact characterizations of the directed homology structure of a neural network architecture are the first of their kind. We show that the directed flag homology of deep networks reduces to computing the simplicial homology of the underlying undirected graph, which is explicitly given by Euler characteristic computations. We also show that the path homology of these networks is non-trivial in higher dimensions and depends on the number and size of the layers within the network. These results provide a foundation for investigating homological differences between neural network architectures and their realized structure as implied by their parameters.