Token embeddings violate the manifold hypothesis

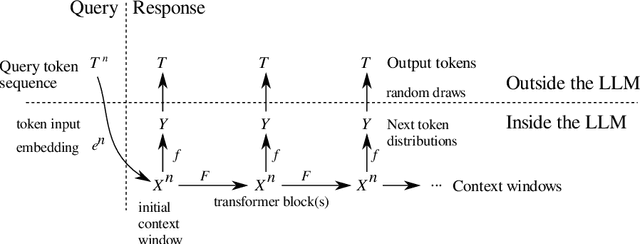
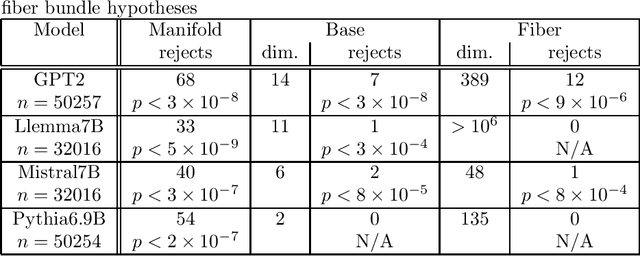
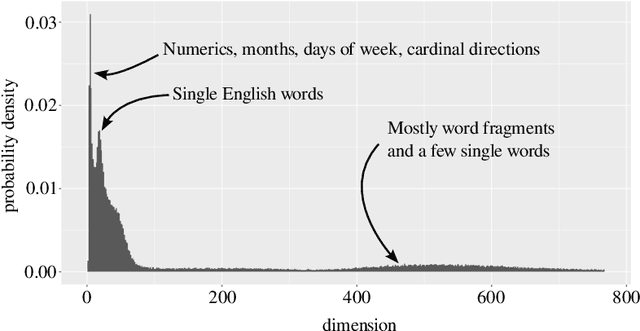
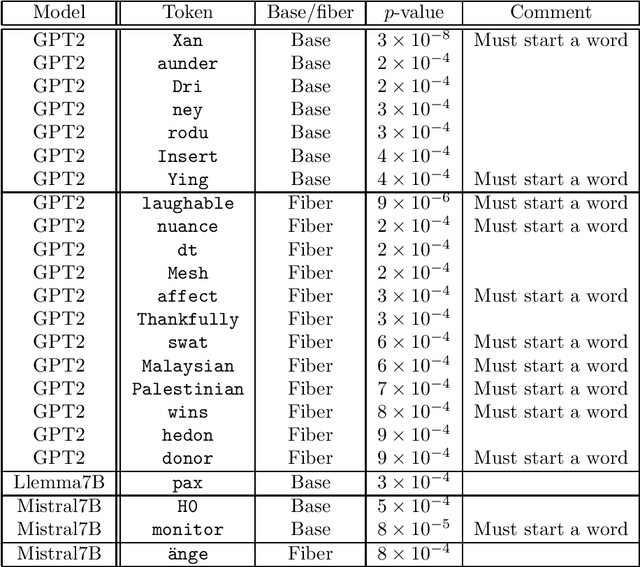
To fully understand the behavior of a large language model (LLM) requires our understanding of its input space. If this input space differs from our assumption, our understanding of and conclusions about the LLM is likely flawed, regardless of its architecture. Here, we elucidate the structure of the token embeddings, the input domain for LLMs, both empirically and theoretically. We present a generalized and statistically testable model where the neighborhood of each token splits into well-defined signal and noise dimensions. This model is based on a generalization of a manifold called a fiber bundle, so we denote our hypothesis test as the ``fiber bundle null.'' Failing to reject the null is uninformative, but rejecting it at a specific token indicates that token has a statistically significant local structure, and so is of interest to us. By running our test over several open-source LLMs, each with unique token embeddings, we find that the null is frequently rejected, and so the token subspace is provably not a fiber bundle and hence also not a manifold. As a consequence of our findings, when an LLM is presented with two semantically equivalent prompts, and if one prompt contains a token implicated by our test, that prompt will likely exhibit more output variability proportional to the local signal dimension of the token.

Probing the topology of the space of tokens with structured prompts

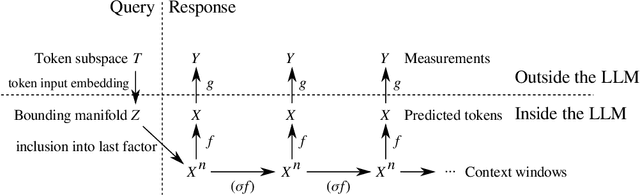
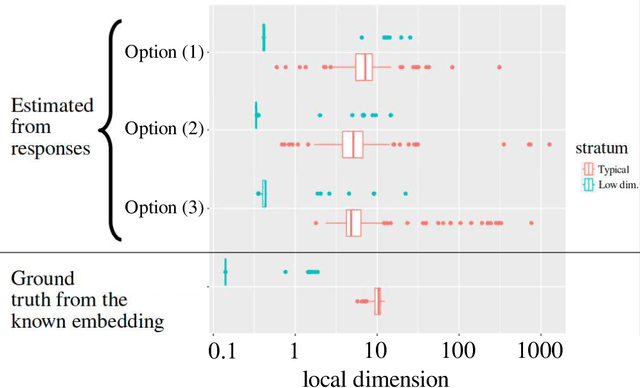
This article presents a general and flexible method for prompting a large language model (LLM) to reveal its (hidden) token input embedding up to homeomorphism. Moreover, this article provides strong theoretical justification -- a mathematical proof for generic LLMs -- for why this method should be expected to work. With this method in hand, we demonstrate its effectiveness by recovering the token subspace of Llemma-7B. The results of this paper apply not only to LLMs but also to general nonlinear autoregressive processes.

The structure of the token space for large language models

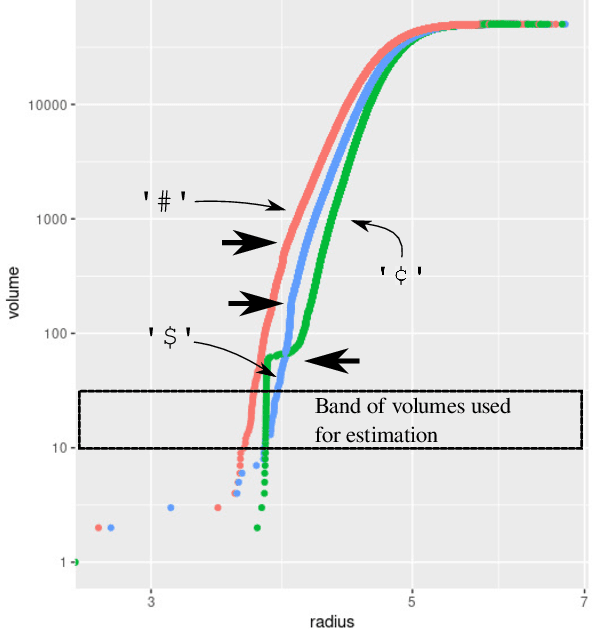
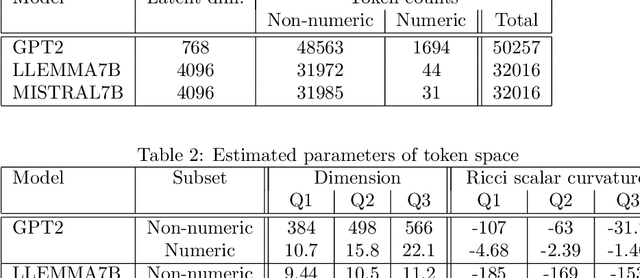
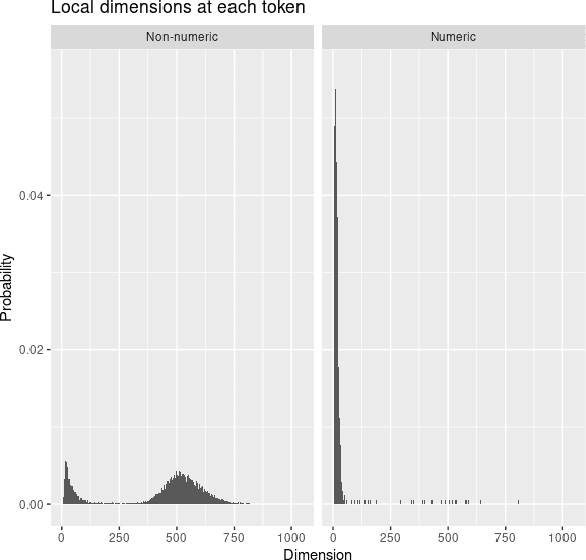
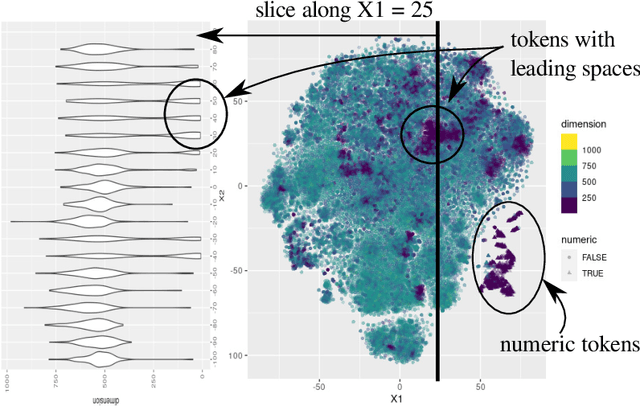
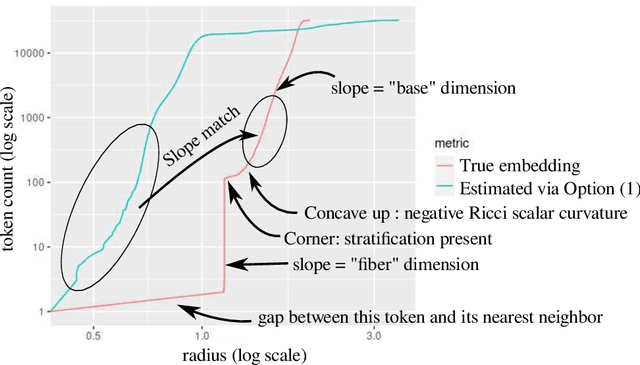
Large language models encode the correlational structure present in natural language by fitting segments of utterances (tokens) into a high dimensional ambient latent space upon which the models then operate. We assert that in order to develop a foundational, first-principles understanding of the behavior and limitations of large language models, it is crucial to understand the topological and geometric structure of this token subspace. In this article, we present estimators for the dimension and Ricci scalar curvature of the token subspace, and apply it to three open source large language models of moderate size: GPT2, LLEMMA7B, and MISTRAL7B. In all three models, using these measurements, we find that the token subspace is not a manifold, but is instead a stratified manifold, where on each of the individual strata, the Ricci curvature is significantly negative. We additionally find that the dimension and curvature correlate with generative fluency of the models, which suggest that these findings have implications for model behavior.

Prospects for inconsistency detection using large language models and sheaves

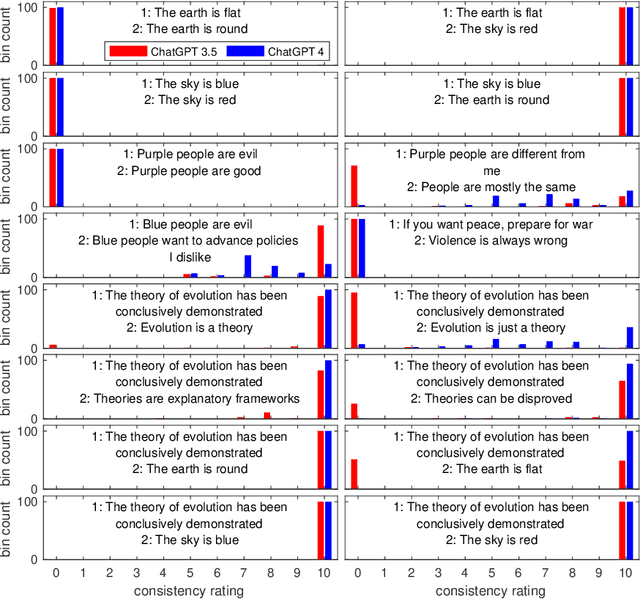
We demonstrate that large language models can produce reasonable numerical ratings of the logical consistency of claims. We also outline a mathematical approach based on sheaf theory for lifting such ratings to hypertexts such as laws, jurisprudence, and social media and evaluating their consistency globally. This approach is a promising avenue to increasing consistency in and of government, as well as to combating mis- and disinformation and related ills.

The Topology of Circular Synthetic Aperture Sonar Targets

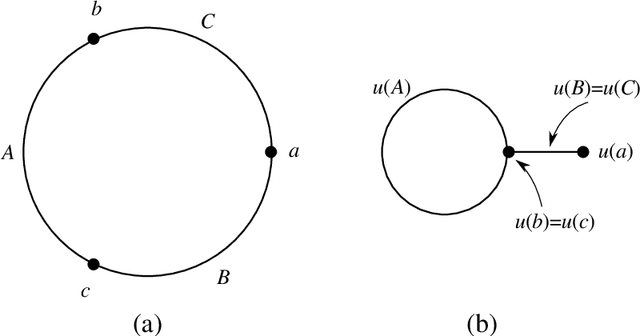
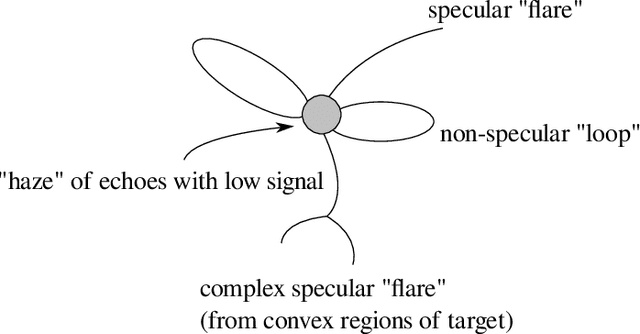
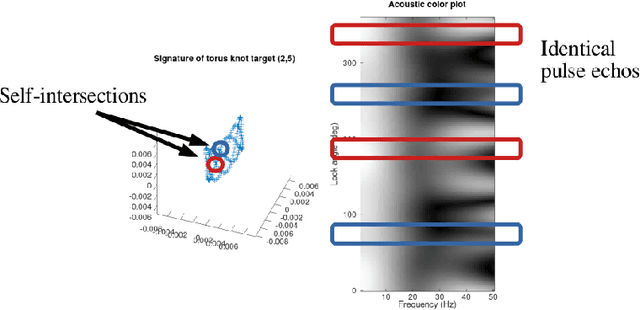
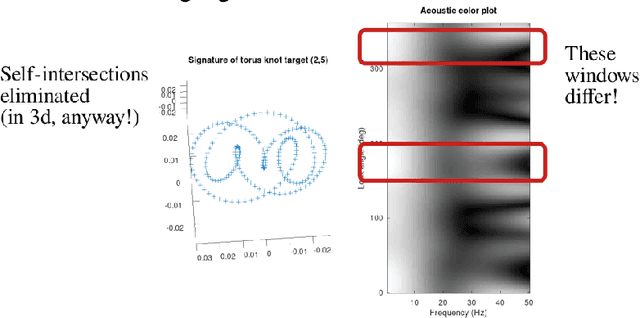
This report presents a connection between the physical acoustics of an object and the topology of the space of echoes resulting from a circular synthetic aperture sonar (CSAS) collection of that object. A simple theoretical model is developed that yields a precise, yet qualitative, description of the space of echoes. This theoretical model is validated in simulation and with experimental data from a laboratory sonar system.

A Topological Lowpass Filter for Quasiperiodic Signals

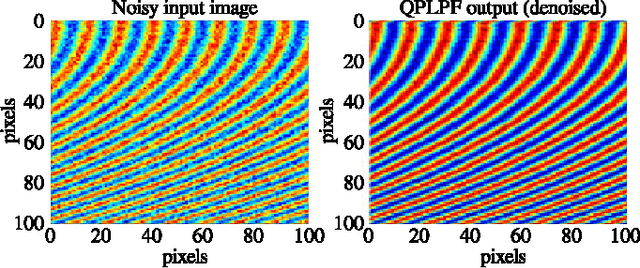
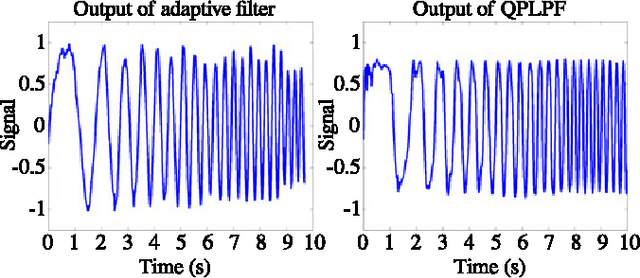
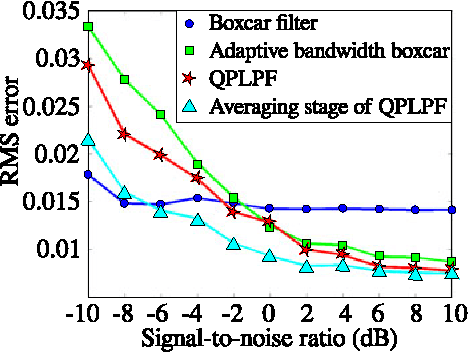
This article presents a two-stage topological algorithm for recovering an estimate of a quasiperiodic function from a set of noisy measurements. The first stage of the algorithm is a topological phase estimator, which detects the quasiperiodic structure of the function without placing additional restrictions on the function. By respecting this phase estimate, the algorithm avoids creating distortion even when it uses a large number of samples for the estimate of the function.