The structure of the token space for large language models
Paper and Code
Oct 11, 2024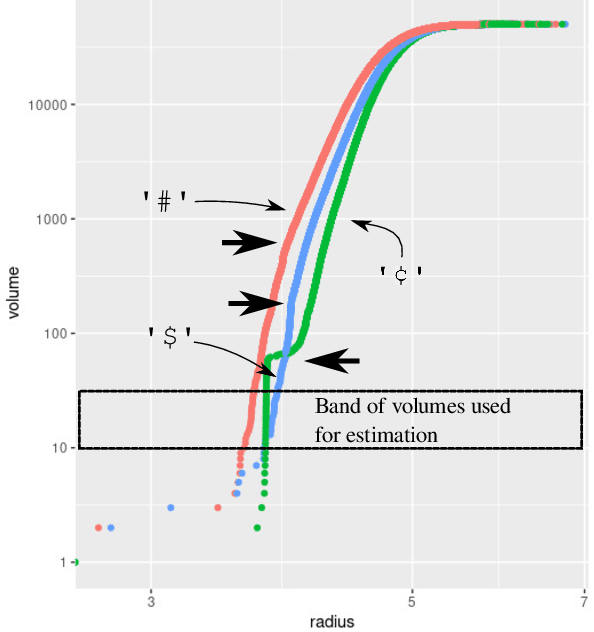
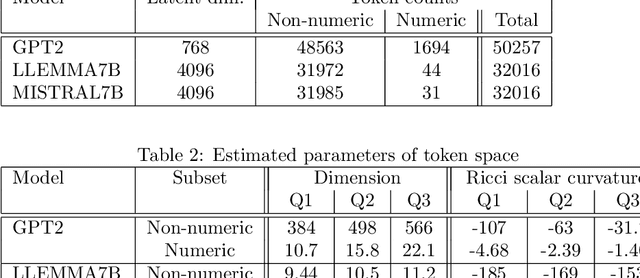
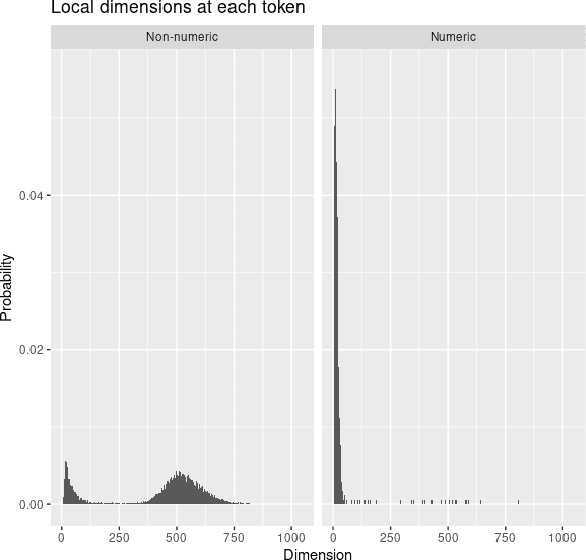
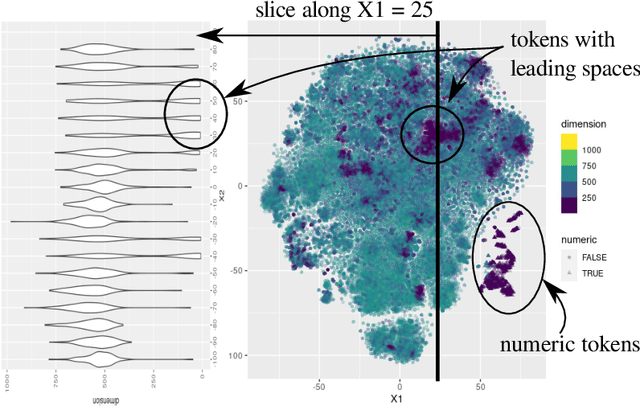
Large language models encode the correlational structure present in natural language by fitting segments of utterances (tokens) into a high dimensional ambient latent space upon which the models then operate. We assert that in order to develop a foundational, first-principles understanding of the behavior and limitations of large language models, it is crucial to understand the topological and geometric structure of this token subspace. In this article, we present estimators for the dimension and Ricci scalar curvature of the token subspace, and apply it to three open source large language models of moderate size: GPT2, LLEMMA7B, and MISTRAL7B. In all three models, using these measurements, we find that the token subspace is not a manifold, but is instead a stratified manifold, where on each of the individual strata, the Ricci curvature is significantly negative. We additionally find that the dimension and curvature correlate with generative fluency of the models, which suggest that these findings have implications for model behavior.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge