Quantized Gromov-Wasserstein

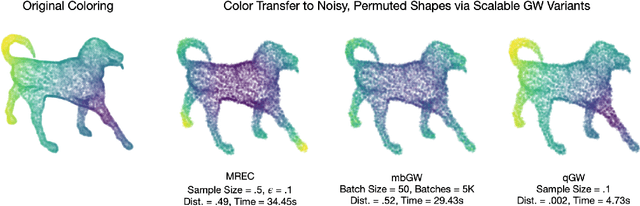
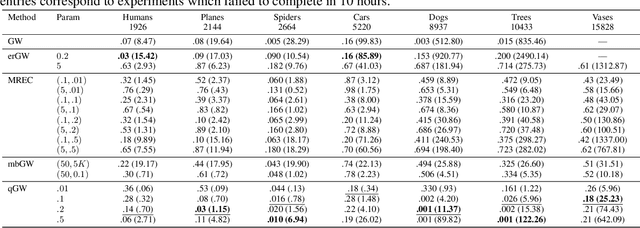
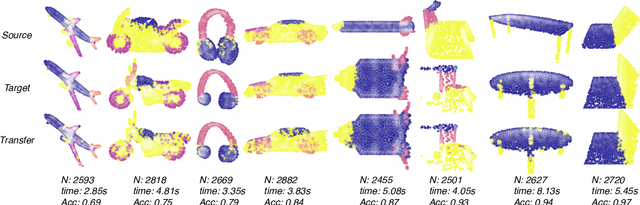
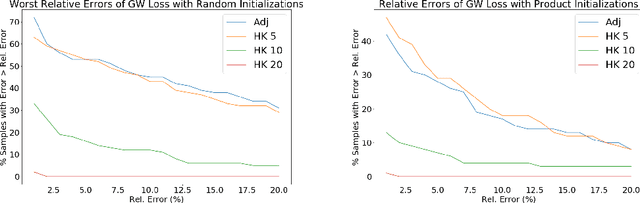
The Gromov-Wasserstein (GW) framework adapts ideas from optimal transport to allow for the comparison of probability distributions defined on different metric spaces. Scalable computation of GW distances and associated matchings on graphs and point clouds have recently been made possible by state-of-the-art algorithms such as S-GWL and MREC. Each of these algorithmic breakthroughs relies on decomposing the underlying spaces into parts and performing matchings on these parts, adding recursion as needed. While very successful in practice, theoretical guarantees on such methods are limited. Inspired by recent advances in the theory of quantization for metric measure spaces, we define Quantized Gromov Wasserstein (qGW): a metric that treats parts as fundamental objects and fits into a hierarchy of theoretical upper bounds for the GW problem. This formulation motivates a new algorithm for approximating optimal GW matchings which yields algorithmic speedups and reductions in memory complexity. Consequently, we are able to go beyond outperforming state-of-the-art and apply GW matching at scales that are an order of magnitude larger than in the existing literature, including datasets containing over 1M points.

Generalized Spectral Clustering via Gromov-Wasserstein Learning

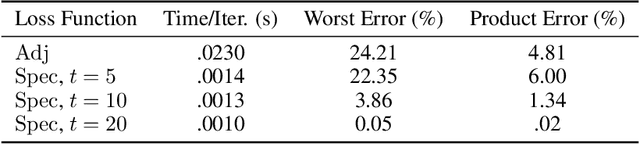
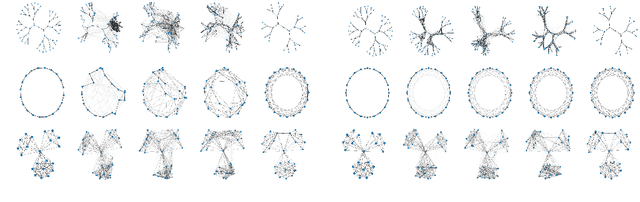
We establish a bridge between spectral clustering and Gromov-Wasserstein Learning (GWL), a recent optimal transport-based approach to graph partitioning. This connection both explains and improves upon the state-of-the-art performance of GWL. The Gromov-Wasserstein framework provides probabilistic correspondences between nodes of source and target graphs via a quadratic programming relaxation of the node matching problem. Our results utilize and connect the observations that the GW geometric structure remains valid for any rank-2 tensor, in particular the adjacency, distance, and various kernel matrices on graphs, and that the heat kernel outperforms the adjacency matrix in producing stable and informative node correspondences. Using the heat kernel in the GWL framework provides new multiscale graph comparisons without compromising theoretical guarantees, while immediately yielding improved empirical results. A key insight of the GWL framework toward graph partitioning was to compute GW correspondences from a source graph to a template graph with isolated, self-connected nodes. We show that when comparing against a two-node template graph using the heat kernel at the infinite time limit, the resulting partition agrees with the partition produced by the Fiedler vector. This in turn yields a new insight into the $k$-cut graph partitioning problem through the lens of optimal transport. Our experiments on a range of real-world networks achieve comparable results to, and in many cases outperform, the state-of-the-art achieved by GWL.

Path homologies of deep feedforward networks

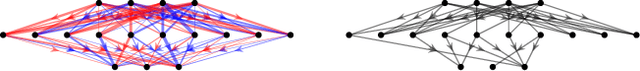
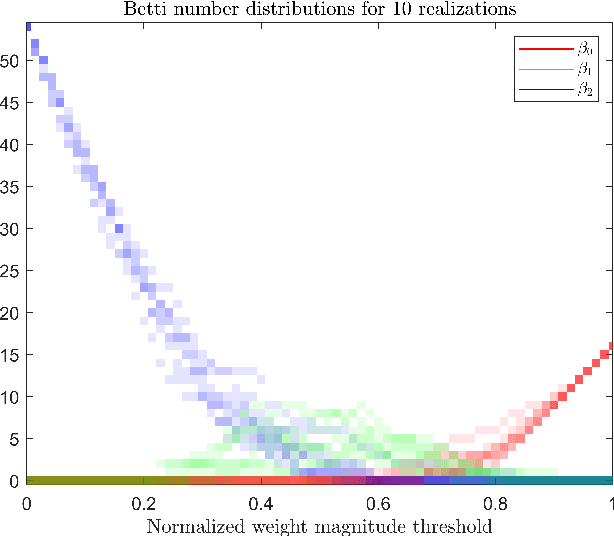
We provide a characterization of two types of directed homology for fully-connected, feedforward neural network architectures. These exact characterizations of the directed homology structure of a neural network architecture are the first of their kind. We show that the directed flag homology of deep networks reduces to computing the simplicial homology of the underlying undirected graph, which is explicitly given by Euler characteristic computations. We also show that the path homology of these networks is non-trivial in higher dimensions and depends on the number and size of the layers within the network. These results provide a foundation for investigating homological differences between neural network architectures and their realized structure as implied by their parameters.

Gromov-Wasserstein Averaging in a Riemannian Framework

We introduce a theoretical framework for performing statistical tasks---including, but not limited to, averaging and principal component analysis---on the space of (possibly asymmetric) matrices with arbitrary entries and sizes. This is carried out under the lens of the Gromov-Wasserstein (GW) distance, and our methods translate the Riemannian framework of GW distances developed by Sturm into practical, implementable tools for network data analysis. Our methods are illustrated on datasets of asymmetric stochastic blockmodel networks and planar shapes viewed as metric spaces. On the theoretical front, we supplement the work of Sturm by producing additional results on the tangent structure of this "space of spaces", as well as on the gradient flow of the Fr\'{e}chet functional on this space.