Generalized Spectral Clustering via Gromov-Wasserstein Learning

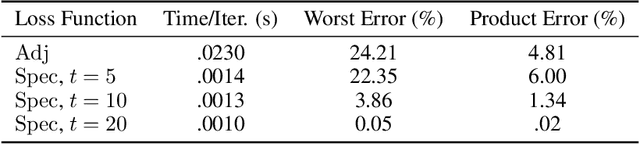
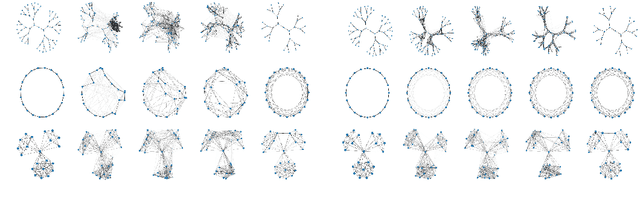
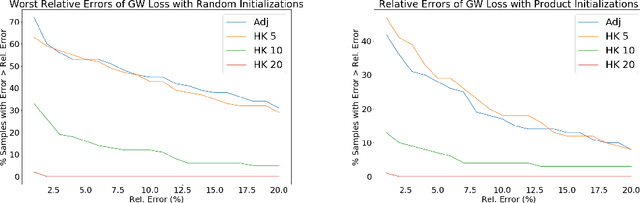
We establish a bridge between spectral clustering and Gromov-Wasserstein Learning (GWL), a recent optimal transport-based approach to graph partitioning. This connection both explains and improves upon the state-of-the-art performance of GWL. The Gromov-Wasserstein framework provides probabilistic correspondences between nodes of source and target graphs via a quadratic programming relaxation of the node matching problem. Our results utilize and connect the observations that the GW geometric structure remains valid for any rank-2 tensor, in particular the adjacency, distance, and various kernel matrices on graphs, and that the heat kernel outperforms the adjacency matrix in producing stable and informative node correspondences. Using the heat kernel in the GWL framework provides new multiscale graph comparisons without compromising theoretical guarantees, while immediately yielding improved empirical results. A key insight of the GWL framework toward graph partitioning was to compute GW correspondences from a source graph to a template graph with isolated, self-connected nodes. We show that when comparing against a two-node template graph using the heat kernel at the infinite time limit, the resulting partition agrees with the partition produced by the Fiedler vector. This in turn yields a new insight into the $k$-cut graph partitioning problem through the lens of optimal transport. Our experiments on a range of real-world networks achieve comparable results to, and in many cases outperform, the state-of-the-art achieved by GWL.