Sheaf theory: from deep geometry to deep learning

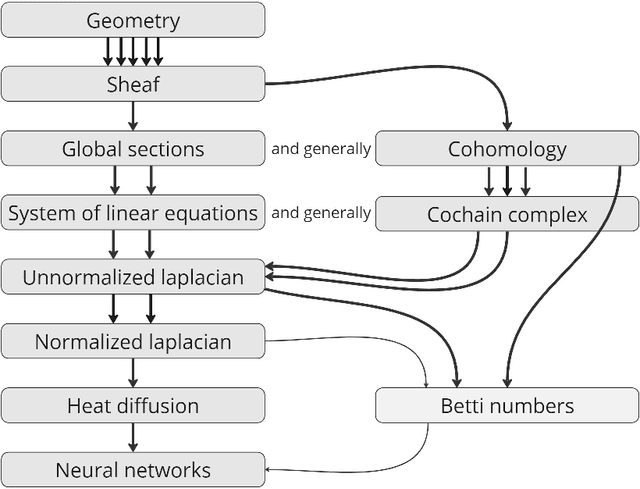
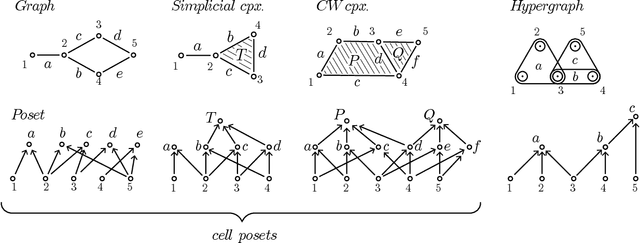
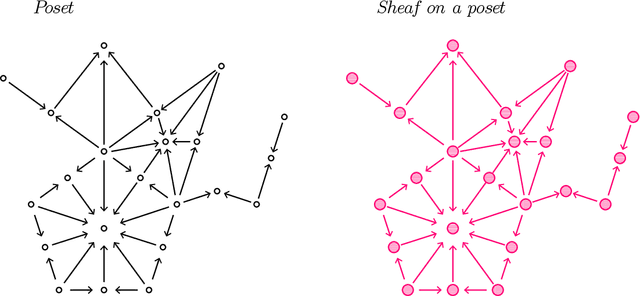
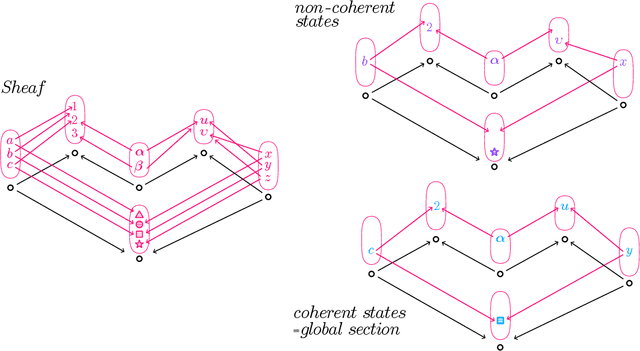
This paper provides an overview of the applications of sheaf theory in deep learning, data science, and computer science in general. The primary text of this work serves as a friendly introduction to applied and computational sheaf theory accessible to those with modest mathematical familiarity. We describe intuitions and motivations underlying sheaf theory shared by both theoretical researchers and practitioners, bridging classical mathematical theory and its more recent implementations within signal processing and deep learning. We observe that most notions commonly considered specific to cellular sheaves translate to sheaves on arbitrary posets, providing an interesting avenue for further generalization of these methods in applications, and we present a new algorithm to compute sheaf cohomology on arbitrary finite posets in response. By integrating classical theory with recent applications, this work reveals certain blind spots in current machine learning practices. We conclude with a list of problems related to sheaf-theoretic applications that we find mathematically insightful and practically instructive to solve. To ensure the exposition of sheaf theory is self-contained, a rigorous mathematical introduction is provided in appendices which moves from an introduction of diagrams and sheaves to the definition of derived functors, higher order cohomology, sheaf Laplacians, sheaf diffusion, and interconnections of these subjects therein.

Topology of cognitive maps

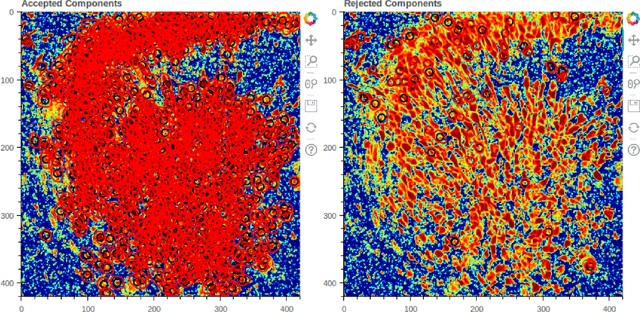
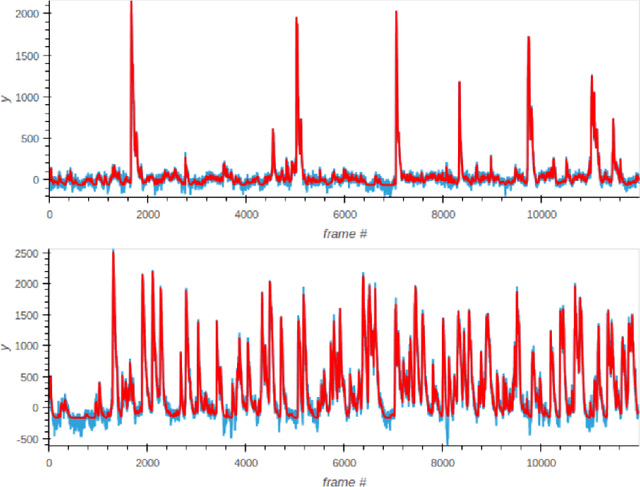
In present paper we discuss several approaches to reconstructing the topology of the physical space from neural activity data of CA1 fields in mice hippocampus, in particular, having Cognitome theory of brain function in mind. In our experiments, animals were placed in different new environments and discovered these moving freely while their physical and neural activity was recorded. We test possible approaches to identifying place cell groups out of the observed CA1 neurons. We also test and discuss various methods of dimension reduction and topology reconstruction. In particular, two main strategies we focus on are the Nerve theorem and point cloud-based methods. Conclusions on the results of reconstruction are supported with illustrations and mathematical background which is also briefly discussed.

Topology and geometry of data manifold in deep learning

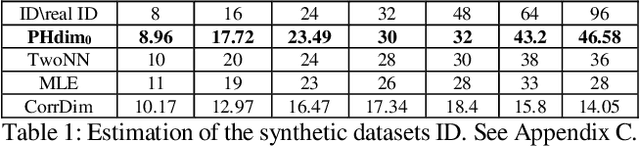
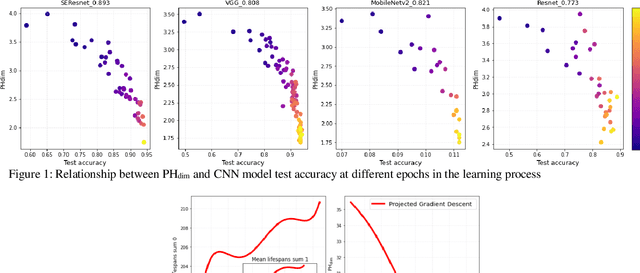
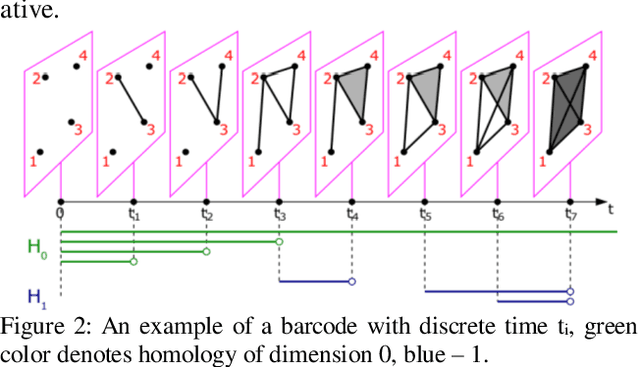
Despite significant advances in the field of deep learning in applications to various fields, explaining the inner processes of deep learning models remains an important and open question. The purpose of this article is to describe and substantiate the geometric and topological view of the learning process of neural networks. Our attention is focused on the internal representation of neural networks and on the dynamics of changes in the topology and geometry of the data manifold on different layers. We also propose a method for assessing the generalizing ability of neural networks based on topological descriptors. In this paper, we use the concepts of topological data analysis and intrinsic dimension, and we present a wide range of experiments on different datasets and different configurations of convolutional neural network architectures. In addition, we consider the issue of the geometry of adversarial attacks in the classification task and spoofing attacks on face recognition systems. Our work is a contribution to the development of an important area of explainable and interpretable AI through the example of computer vision.